满二叉树和完全二叉树

满二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的层数为h，且结点总数是(2^k) -1 ，则它就是满二叉树或完美二叉树。
完全二叉树，若一颗二叉树除最后一层外，其他层的节点都是满的，且最后一层节点是从左到右的一排连续的，那么这样的二叉树为完全二叉树。

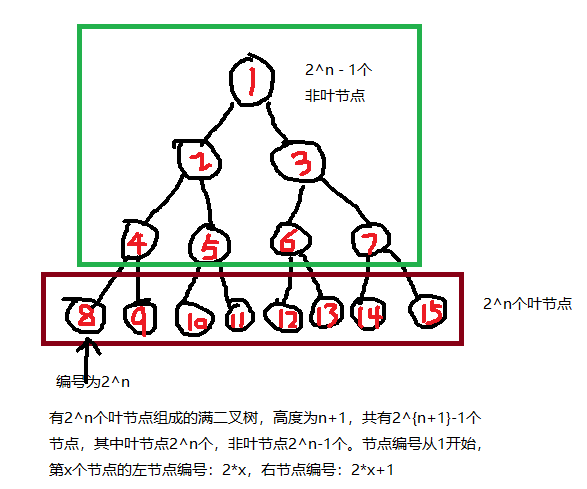
有 $2^n$ 个叶节点的（根节点编号为1）满二叉树有以下性质：

1、共有 $n+1$ 层，$2^{n+1}-1$个节点，由 $2^n-1$ 个节点和 $2^n$个叶节点组成。
2、第1个叶节点的编号为 $2^n$ ,最后一个叶节点的编号为 $2^n-1$，共 $2^n$ 个叶节点。
3、编号为 x 的节点，它的左节点为 $2\cdot x$,右节点为$2\cdot x+1$

习题 洛谷P4715 ：

题意：有 $2^n(n\le7)$ 个国家参加世界杯决赛圈且进入淘汰赛环节。我经知道各个国家的能力值，且都不相等。能力值高的国家和能力值低的国家踢比赛时高者获胜。1 号国家和 2 号国家踢一场比赛，胜者晋级。3 号国家和 4 号国家也踢一场，胜者晋级……晋级后的国家用相同的方法继续完成赛程，直到决出冠军。给出各个国家的能力值，请问亚军是哪个国家？

输入：
3
4 2 3 1 10 5 9 7
输出：
1

注释版代码

#include <cstdio>
using namespace std;
const int N=260;//最多2^h-1个结点，h是深度 = n+1
int val[N],win[N];
int n;
void dfs(int x){
    if(x>=1<<n) return;//若x是叶子结点就不在继续遍历了
    dfs(2*x);//递归左子树
    dfs(2*x+1);//递归右子树
    int l=val[2*x],r=val[2*x+1];//l,r为左右子树的值
    if(l>r){//若左点获胜则把左点值和编号保存在x里面
        val[x]=l;
        win[x]=win[2*x];
    }
    else{//若右点获胜则把右点的值及编号保存在x里面
        val[x]=r;
        win[x]=win[2*x+1];
    }
}
int main(){
    scanf("%d",&n);
    for(int i=0;i<1<<n;i++){
        scanf("%d",&val[i+(1<<n)]);//把各国家的能力值保存到叶子节点
        win[i+(1<<n)]=i+1;//初始化叶子节点为各个国家的编号
    }
    dfs(1);//从根节点开始递归
    printf("%d\n",val[2]>val[3]?win[3]:win[2]);//左右比较，小的是亚军，大的是冠军
    return 0;
}

补充说明

1、普通二叉树（有空缺的），再用一维数组简单模拟会造成大量的空间浪费，及空间不足的问题，改用2个数组分别模拟左子树和右子树。
2、世界杯共有32个球队，也是 $2^5$ ,否则就不是满二叉树，那样会有球队直接晋级决赛了。
3、可以通过控制递归的退出语句，精确定位递归后的代码从那一层节点开始执行，这题是控制到非叶节点开始执行。