<--------------【Loading…】

正在更新中！

前言

学了这么久发现自己还不会写平衡树相关的板子，所以来再顺一遍思路。

$$\Huge【平衡树】目录$$

一、旋转 Treap

定义

先献上一个很好看的公式：$Treap = Tree + Heap$。
这是什么意思呢？Treap 这个东西，它同时具有二叉搜索树和堆的美妙性质。

二叉搜索树的性质（$val$ 的中序遍历是有序序列）这里就不多说了，至于堆的性质：
子节点的 $priority$ 比父节点要大或小（满足堆的性质）。
这里先对每个点定义 $priority$，显然如果它直接赋值为 $val$ 仍会导致极端数据，即产生一条链。
那么就给他一个随机值以保证复杂度。（盗窃一张 OI-Wiki 的图，以小根堆为例）

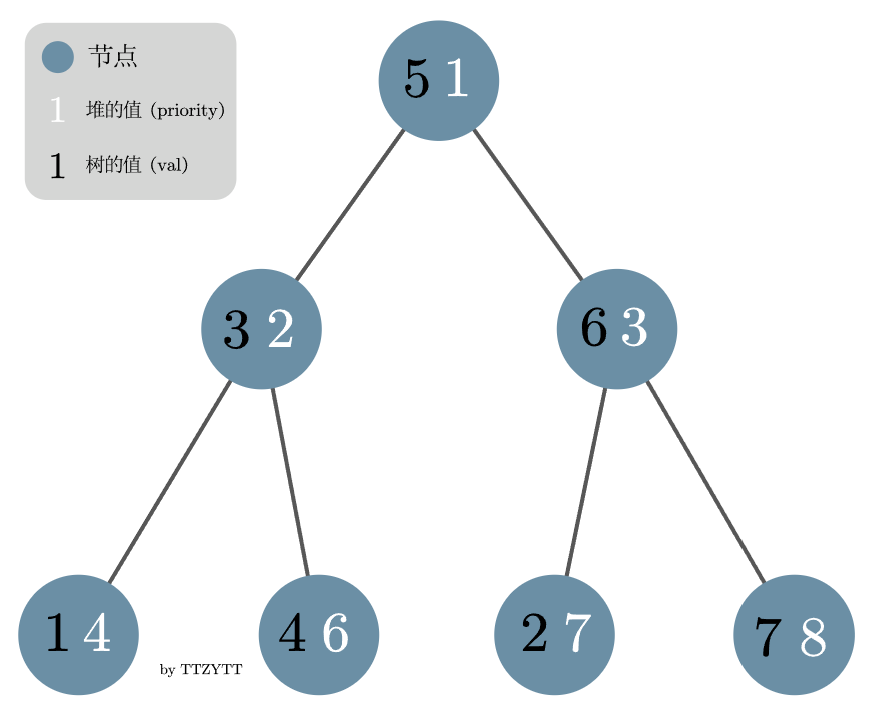
那么问题来了，如何同时维护二叉搜索树和堆这两个性质呢？

• 旋转 Treap——旋转
• 无旋 Treap——分裂、合并

这里暂时只讲解旋转 Treap。

基本操作

旋转（the most important）

好像在这里炫耀我的三脚猫英语不是很合适啊。

旋转 Treap，顾名思义，通过旋转以维护平衡。
众所周知，Treap 也是 二叉搜索树 的一种，所以它发明出来肯定要先符合二叉搜索树的性质，再在这个基础上进行优化。
因此，满足二叉搜索树性质优先级更高。

要在二叉搜索树性质的基础上，再维护堆的性质，这里旋转操作分为两种：左旋和右旋。

• 保证二叉搜索树的性质，同时将旋转方向相反方向的儿子换成根节点。

什么意思呢？由于笔者手残且懒，不想画图，所以我们再次借鉴一下 OI-Wiki 的图：

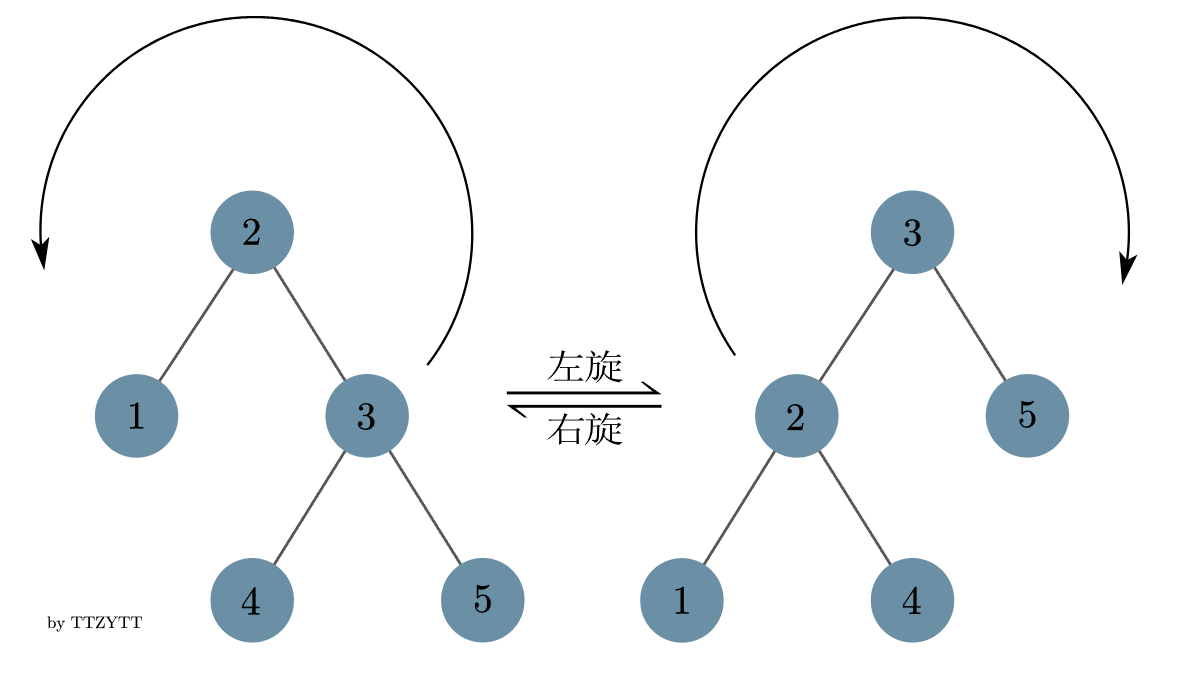
容易发现，旋转前后的中序遍历是不变的，左旋右旋是相互的。
例如左旋可以理解为，把根节点往左边沉下去，与之对应的，右节点为了保持平衡就要浮上来，这个时候右儿子的左儿子会和原根节点撞在一起，所以就只好把它接在原根节点的右儿子上了。（个人理解，虽然可能不是很形象）右旋反之。

PS：这玩意儿我愣是看了半天，希望这种理解方法可以帮助你们快速记住旋转的原理。

插入

你看过上面的前置知识 BST 了吗？其实原理一样，只不过需要注意维护堆的性质。

• 从根节点开始遍历。
• 若当前节点为空，则在这个地方创建一个点。
• 否则，若要插入的小于当前节点，往左走。
• 否则，若要插入的大于当前节点，往右走。
• 否则，即插入的等于当前节点，cnt 加 $1$。
• 到达空节点创建完成之后，就要回溯，同时保持堆的性质。
  • 简单地说，若一个点左儿子的 $priority$ 比它大，则左旋，让左儿子代替它。
  • 反之亦然，若一个点右儿子的 $priority$ 比他大，则右旋，让右儿子代替它。
  • 一定要记得更新节点信息！！

删除

这个我一直觉得比较复杂……
这里采用的方法是：

• 从根节点开始遍历。
• 如果当前点与要删除的元素相同
  • 如果数量大于 $1$，直接减 $1$ 即可。——End
  • 否则，如果它是叶子节点，直接删掉。——End
  • 否则，它不是叶子节点。
    • 若右子树为空或左儿子的 $priority$ 大于右儿子
      • 则右旋，让左儿子继承它的位置。
      • 这时候该元素被扔到右子树，所以递归右子树删除。
    • 否则
      • 则左旋，让右儿子继承它的位置。
      • 这时候该元素被扔到左子树，所以递归左子树删除。
• 如果当前点与要删除的元素不同
  • 按照二叉搜索树的搜索方法：
  • 若要删的小于当前节点权值，往左边走。
  • 若要删的大于当前节点权值，往右边走。
• 一定要记得更新节点信息！！！

依照上面的方法即可写出代码模板（后面会放）。

查询元素排名

同 二叉搜索树。

查询某排名的元素

同 二叉搜索树。

查询前驱（严格小于 x 的最大元素）

• 从根节点开始。
• 若当前节点为空，则返回负无穷。
• 若当前节点权值大于等于 $x$，则往左子树搜索。
• 否则取当前节点和右子树搜索结果的最大值。

查询后继（严格大于 x 的最小元素）

与查询前驱思路大致相同，不再赘述。

总结与归纳

旋转 Treap 的大部分都是和二叉搜索树差不多的，只不过加入了一个 $priority$ 以优化复杂度。
代码中 zag 是左旋，zig 是右旋，可以记忆为 a 在左边，i 在右边（键盘上的位置）。
旋转后要记得 pushup 更新节点信息，当然是从下往上更新啦，注意更新顺序。

代码模板

这里采用大根堆，因为小根堆出了点问题还没解决。

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 15, INF = 0x3f3f3f3f;

int n;
struct Treap {
    int ls, rs;
    int val, prio;  //权值、随机赋值
    int cnt, sz;    //出现次数、子树大小
} tr[N];

int rt, idx = 0;

void pushup(int u) {    //统计以 u 为根子树的信息
    tr[u].sz = tr[tr[u].ls].sz + tr[tr[u].rs].sz + tr[u].cnt;   //一定不要忘记加上它自己的 cnt！
    //是加 cnt，不是加 1！因为一个元素不只出现一次！！
}

int get_node(int val) {   //新建一个节点，元素为 val，返回其编号
    tr[++idx].val = val;
    tr[idx].prio = rand();
    tr[idx].cnt = tr[idx].sz = 1;
    return idx;
}

void zag(int &u) {    //左旋
    int v = tr[u].rs;   //u 的右儿子
    tr[u].rs = tr[v].ls, tr[v].ls = u, u = v;
    pushup(tr[u].ls), pushup(u);
}

void zig(int &u) {
    int v = tr[u].ls;
    tr[u].ls = tr[v].rs, tr[v].rs = u, u = v;
    pushup(tr[u].rs), pushup(u);
}

void init() {
    get_node(-INF), get_node(INF);  //设置两个哨兵，减少查询的特判
    rt = 1; tr[1].rs = 2;   //设置两个新节点之间的关系
    if (tr[1].prio < tr[2].prio) zag(rt);   //显然要维护堆的性质
}

void insert(int &u, int val) {
    if (!u) u = get_node(val);
    else if (val == tr[u].val) tr[u].cnt++;
    else if (val < tr[u].val) {
        insert(tr[u].ls, val);
        if (tr[tr[u].ls].prio > tr[u].prio) zig(u);
    } else if (val > tr[u].val) {
        insert(tr[u].rs, val);
        if (tr[tr[u].rs].prio > tr[u].prio) zag(u);
    }
    pushup(u);
}

void remove(int &u, int val) {
    if (!u) return;
    if (val == tr[u].val) {
        if (tr[u].cnt > 1) tr[u].cnt--;
        else if (!tr[u].ls && !tr[u].rs) u = 0;
        else {
            if (!tr[u].rs || tr[tr[u].ls].prio > tr[tr[u].rs].prio) {
                zig(u);
                remove(tr[u].rs, val);
            } else {
                zag(u);
                remove(tr[u].ls, val);
            }
        }
    } else {
        if (val < tr[u].val) remove(tr[u].ls, val);
        else remove(tr[u].rs, val);
    }
    pushup(u);
}

int get_val_by_rank(int u, int rank) {  //通过排名找元素
    if (!u) return INF;
    if (tr[tr[u].ls].sz >= rank) return get_val_by_rank(tr[u].ls, rank);
    else if (tr[tr[u].ls].sz + tr[u].cnt < rank) return get_val_by_rank(tr[u].rs, rank - tr[tr[u].ls].sz - tr[u].cnt);
    else return tr[u].val;
}

int get_rank_by_val(int u, int val) {   //通过元素找排名
    if (!u) return 0;
    if (val == tr[u].val) return tr[tr[u].ls].sz + 1;
    if (val < tr[u].val) return get_rank_by_val(tr[u].ls, val);
    return tr[tr[u].ls].sz + tr[u].cnt + get_rank_by_val(tr[u].rs, val);
}

int get_pre(int u, int val) {   //前驱
    if (!u) return -INF;
    if (val <= tr[u].val) return get_pre(tr[u].ls, val);
    return max(tr[u].val, get_pre(tr[u].rs, val));
}

int get_nxt(int u, int val) {   //后继
    if (!u) return INF;
    if (val >= tr[u].val) return get_nxt(tr[u].rs, val);
    return min(tr[u].val, get_nxt(tr[u].ls, val));
}

int main() {
    srand(time(0));
    scanf("%d", &n);
    init();
    while (n--) {
        int opt, x; scanf("%d%d", &opt, &x);
        if (opt == 1) {
            insert(rt, x);
        } else if (opt == 2) {
            remove(rt, x);
        } else if (opt == 3) {
            printf("%d\n", get_rank_by_val(rt, x) - 1); //由于有哨兵，所以会有1的误差
        } else if (opt == 4) {
            printf("%d\n", get_val_by_rank(rt, x + 1));
        } else if (opt == 5) {
            printf("%d\n", get_pre(rt, x));
        } else {
            printf("%d\n", get_nxt(rt, x));
        }
    }
    return 0;
}