<--------------【Loading…】
正在更新中!
前言
学了这么久发现自己还不会写平衡树相关的板子,所以来再顺一遍思路。
二、Splay 树
这个让我又爱又恨的死东西!
Splay 树由 Daniel Sleator 和 Robert Tarjan 于 1985 年发明。
我最讨厌 Tarjan 了。发明这么多算法结果都看不懂!
(好好好写完这篇博客我就懂了)
废话不多说,直接开冲!
定义
Splay 树又称伸展树,也是二叉搜索树的一种,因此它也具有二叉搜索树的性质。它能在 $O(\log n)$ 的时间复杂度内完成基础操作,并通过优化操作保持树的平衡,不至于退化为链。
与 Treap 不同,我们对每个节点不用 ls、rs 两个变量表示它的儿子,而是用 s[2] 数组来记录它的左右儿子。
同时要记录它的父亲节点 p。
因为 Splay 的旋转操作合并为一个函数比较好写,这样不用特判,可以直接用位运算解决左右问题……(?好像差不多吧)
其余部分记录的信息与 Treap 大致相同,例如 val 节点权值、sz 子树大小等,根据实际问题要维护不同的信息。
基础操作
旋转
Splay 树维护平衡的操作是旋转。
与 Treap 相同,分为左旋和右旋,它需要保证:
- 旋转后中序遍历不变。(不破坏二叉搜索树的性质)
- 旋转后节点信息要正确,同时记得修改根节点。
(作者手残不会画图,所以继续用 OI-Wiki 的)
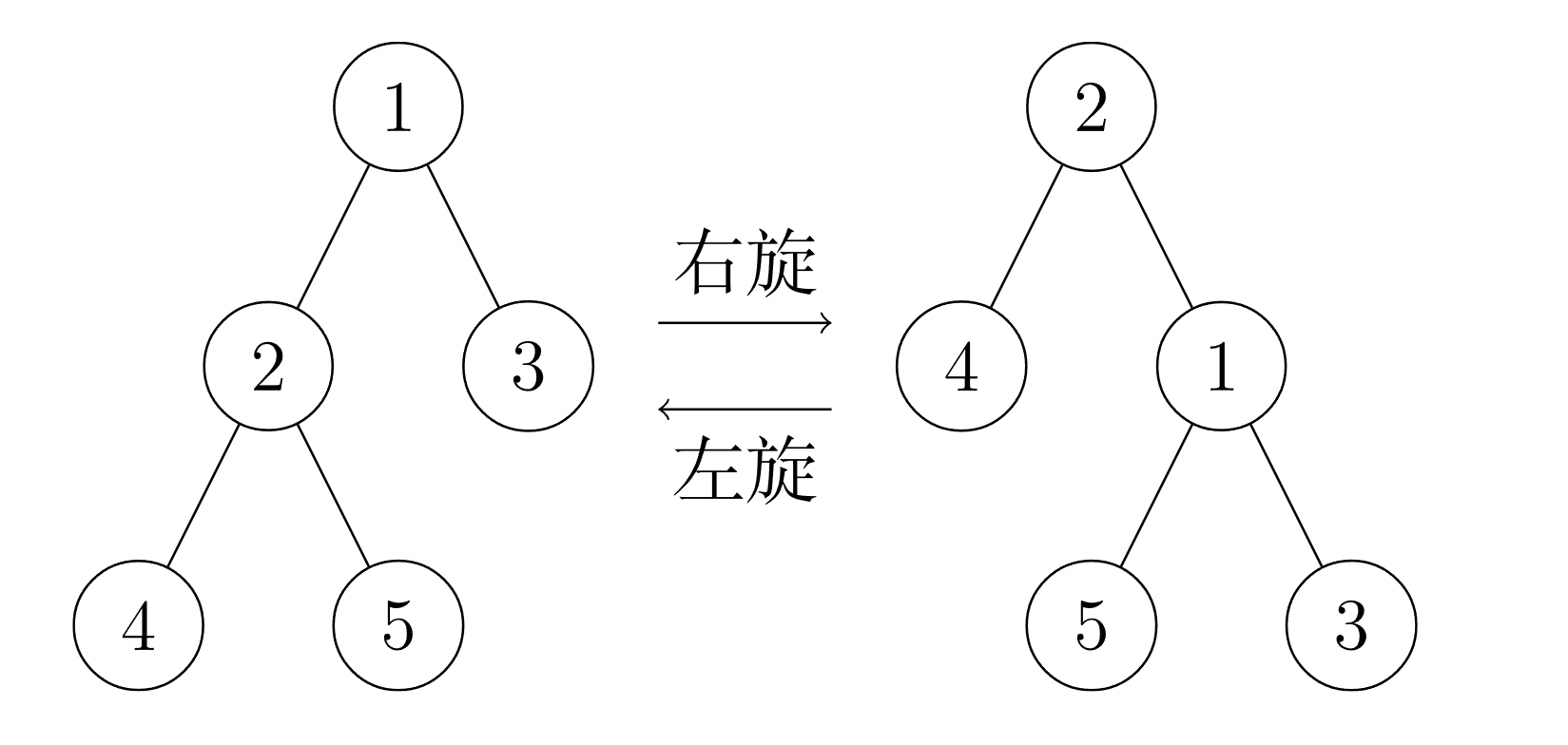
因此代码大致是与 Treap 相同的,但在 Splay 中,我们维护信息主要是把一个节点旋转到根,所以旋转操作是为了把一个节点往上提一层。
因此我们不再是对父节点旋转,而是对我们要上提的节点进行旋转,也正是由于这个原因,我们对每个结点需要记录它的 p 父节点。
先把代码扔上来:
void rotate(int x) { //旋转操作
int y = tr[x].p, z = tr[y].p;
bool k = tr[y].s[1] == x; //k=0表示x是y的左儿子,否则是右儿子
tr[z].s[tr[z].s[1] == y] = x, tr[x].p = z;
tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y;
tr[x].s[k ^ 1] = y, tr[y].p = x;
push_up(y); push_up(x);
}
这里我们要把 $x$ 节点往上提,$x$ 的父节点是 $y$,$y$ 的父节点是 $z$。
设一个布尔变量 $k$,若 $x$ 是 $y$ 的左儿子,则 $k=0$,否则 $k=1$。
若 $k=0$($x$ 是 $y$ 左儿子)则显然右旋,反之亦然。因此 $x$ 的位置与旋转方向是相反的。
所以下文与旋转方向相同是 k ^ 1,与旋转方向相反是 k。
- 从上往下更新,先把 $z$ 的儿子 $y$ 替换为 $x$(把 $x$ 提上来了),同时也更新 $x$ 的父亲为 $z$。
- 然后 $y$ 要接管 $x$ 的儿子,与旋转相同方向的儿子要转给 $y$ 与旋转方向相反的位置。
- 和 Treap 一样,向哪边旋转就相当于把 $y$ 向哪边沉,所以 $y$ 要变成与旋转方向相同那边的 $x$ 的儿子,记得更新 $y$ 的父亲为 $x$。
靠自己感性理解吧
建议每次都把图画出来再去想怎么写代码,写多了后面就肌肉记忆了。
Splay
没错,这个操作叫做 Splay。
每次操作一个节点后要把它旋转到根节点。
这个操作的核心就是对 $x$ 节点不断旋转 旋转跳跃渡劫飞升 往上提。
Tarjan 大神的魅力所在:
这里需要分类讨论六种情况(准确地说,三类,每类两种),但是代码极为简短。
- 当 $x$ 的父节点为根:
- 直接将 $x$ 左旋。
- 直接将 $x$ 右旋。
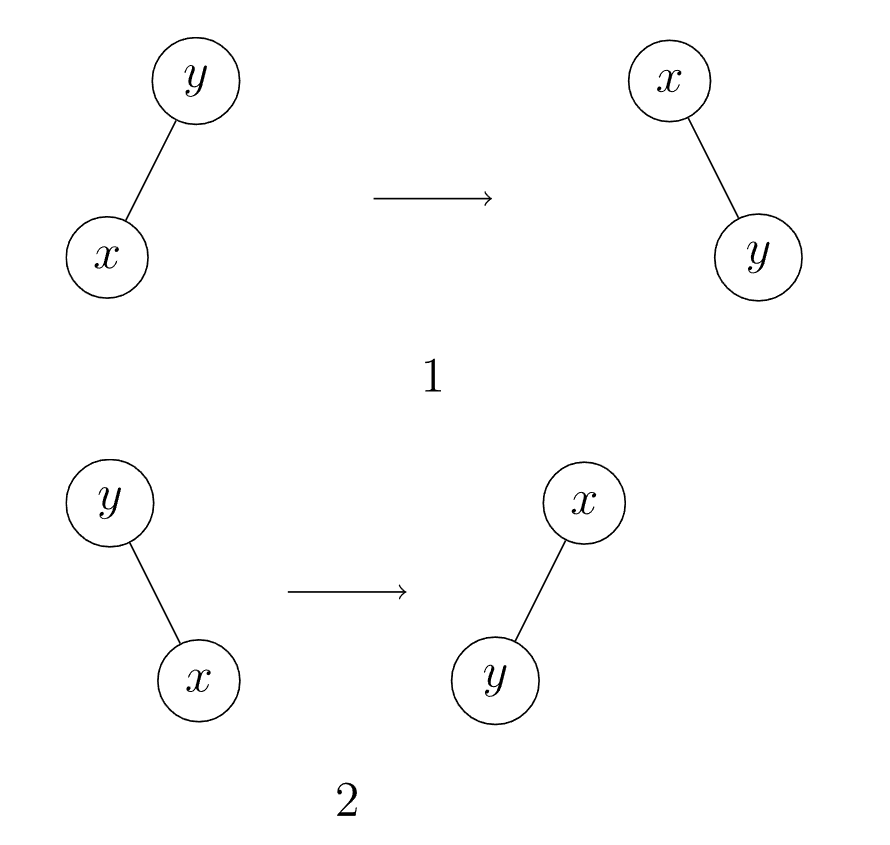
- 当 $x$ 的父节点不为根:
- 他们都作为左儿子或都作为右儿子。
- 先把 $y$ 翻上去,再把 $x$ 翻上去。
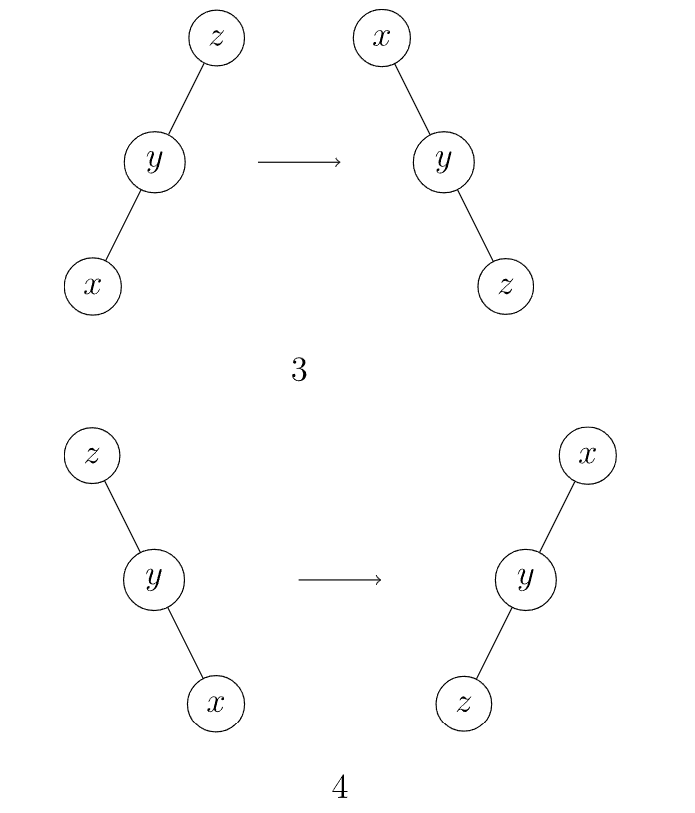
- 他们一个是左儿子,一个是右儿子。
- 先把 $x$ 翻上来,再把 $x$ 再次翻上来。
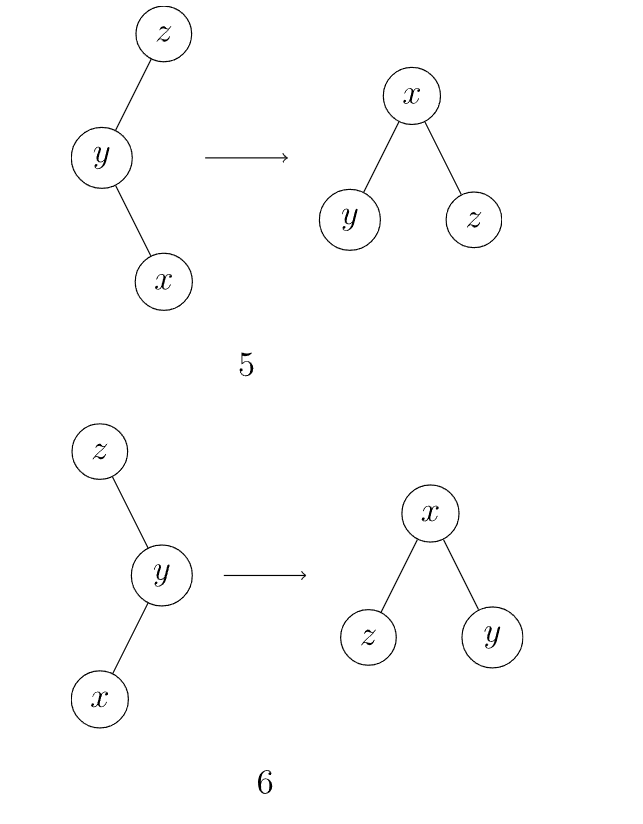
- 他们都作为左儿子或都作为右儿子。
代码确实很短。
下面代码中是实现将 $x$ 旋转到 $k$ 下面,成为 $k$ 的一个儿子。
PS:若 $k=0$ 则旋转到根。
void splay(int x, int k) {
while (tr[x].p != k) { //x 要旋转到 k 的儿子
int y = tr[x].p, z = tr[y].p;
if (z != k) { //判定是否只需要翻转一次
if ((tr[y].s[1] == x) ^ (tr[z].s[1] == y)) rotate(x); //如果不同侧,对应上文情况 2-2
else rotate(y); //如果同侧,对应上文 2-1
}
rotate(x); //对应上文情况 1
}
if (!k) root = x; //标记旋转到根
}
通过势能分析,一次 Splay 操作均摊复杂度为 $O(\log n)$,笔者不是很会证明……有兴趣可以参考 Oi-Wiki。
感性理解一下:树高在最优状态是 $\log n$ 级别,每一次旋转操作显然是 $O(1)$,并且把一个节点提到根,因此 Splay 操作的总复杂度应该是 $O(\log n)$ 级别的。
查找元素
- 从根节点开始。
- 由于 Splay 具有二叉搜索树的性质,将查找元素与当前节点元素作比较。
- 若查找元素小于当前节点元素,往左走。
- 若查找元素大于当前节点元素,往右走。
- 若等于,则说明找到了。
- 若找到空节点,说明不存在。
void find(int x) { //找到元素 x 的位置,把它旋转到根
if (!rt) return; //树都空了还有什么好找的
int u = rt;
while (tr[u].val != x && u) u = tr[u].s[x > tr[u].val];
if (u) splay(u, 0); //旋转到根
}
插入元素
与查找元素大致相同。
若能查找到这个元素,则直接在该节点修改数据即可。
若不能查找到它,我们最后一个访问的节点就是它的父亲(二叉搜索树的性质),所以在下面新建一个叶子节点,并连接它和它的父亲。
void insert(int x) {
int u = rt, fa = 0; //当前节点与它的父亲
while (tr[u].val != x && u) fa = u, u = tr[u].s[x > tr[u].val]; //不断往下找
if (u) tr[u].cnt++; //已经存在的元素
else {
u = ++tot;
if (fa) tr[fa].s[x > tr[fa].val] = u;
tr[u].p = fa;
tr[u].val = x;
tr[u].sz = tr[u].cnt = 1;
}
splay(u, 0); //一定不要忘记这个,保持平衡性的基础
}
$\large题外话$
接下来的操作让我非常摸不着头脑。
有些人是这样做的:
- 对于删除操作,先把元素转到根,然后删掉他,然后合并左右子树。
- 对于前驱后继,相当于你先插入这个数,然后在左子树搜最大的或者在右子树搜最小的,然后再删除这个数。
- 总结:学会前驱后继需要先学会删除操作。
另一些人是这样的:
- 对于删除操作,你先找到它的前驱,扔到根节点。然后再找到他的后继,旋转到根节点(前驱)底下。
- 由于后继比前驱大,所以它在前驱(根)的右子树,由于要删的元素比后继小,所以它在后继的左子树,且这个左子树一定只有一个节点,因为二叉搜索树的中序遍历是有序的。
- 于是你直接删这个根的右儿子的左儿子就可以了。
- 对于前驱后继,先执行 find 找到这个元素,再在左子树找最大或右子树找最小。
- 总结:学会删除操作需要先学会前驱后继。
这两种做法显然都是对的,所以任意实现哪个都行。
这里以第二种为例。
查询前驱
先把这个数转到根节点。
此时比它小的都在它左子树,比它大的都在它右子树。
查询前驱即在左子树找最大的数,也就是从它的左儿子开始一路往右找最大的数。
int pre(int x) {
find(x); //找到它并把它旋转到根
u = tr[u].s[0];
while (tr[u].s[1]) u = tr[u].s[1];
return u; //为了方便删除操作,返回编号而非权值
}
查询后继
与上面同理,不再赘述。
int nxt(int x) {
...
}
删除元素
如上文所说:
- 把它的前驱转到根节点。
- 把它的后继转到根节点的右儿子。
- 删除根节点的右儿子的左儿子。
void remove(int x) {
int Pre = pre(x);
int Nxt = nxt(x);
splay(Pre, 0); splay(Nxt, rt);
int u = tr[tr[rt].s[1]].s[0]; //根节点的右儿子的左儿子,即后继的左儿子 tr[Nxt].s[0];
if (tr[u].cnt > 1) {
tr[u].cnt--;
splay(u, 0);
}
else tr[tr[rt].s[1]].s[0] = 0; //断开连接,删除节点
}
查询元素排名
相对 Treap 来说,就变得十分简单。
直接把这一元素旋转到根节点即可,答案即为它左子树的大小。
int get_rank_by_val(int x) {
splay(find(x), 0);
return tr[tr[rt].s[0]].sz;
}
查询排名为 k 的元素
与 Treap 相同,不再赘述。
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 15;
const int INF = 0x3f3f3f3f;
int n, tot, rt;
struct Splay {
int p, s[2];
int val;
int cnt, sz;
} tr[N];
void pushup(int u) {
tr[u].sz = tr[tr[u].s[0]].sz + tr[tr[u].s[1]].sz + tr[u].cnt;
}
void rotate(int x) { //把 x 节点往上旋转一层
int y = tr[x].p, z = tr[y].p;
bool k = (x == tr[y].s[1]); //k=0表示x是y的左儿子,否则是右儿子
//从上往下更
tr[z].s[tr[z].s[1] == y] = x, tr[x].p = z;
tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y;
tr[x].s[k ^ 1] = y, tr[y].p = x;
pushup(y), pushup(x);
}
void splay(int x, int k) { //把 x 转到 k 下面
while (tr[x].p != k) {
int y = tr[x].p, z = tr[y].p;
if (z == k) rotate(x);
else {
if ((x == tr[y].s[1]) ^ (y == tr[z].s[1])) rotate(x); //折线型异侧
else rotate(y); //直线型同侧
rotate(x); //还要再旋转一次
}
}
if (k == 0) rt = x; //记得更新根节点
}
int find(int x) { //查找一个元素 返回编号
int u = rt;
while (tr[u].val != x && tr[u].s[x > tr[u].val]) {
u = tr[u].s[x > tr[u].val];
}
return u; //不一定搜得到,元素可能不存在
}
void insert(int x) {
int u = rt, fa = 0;
while (tr[u].val != x && u) {
fa = u, u = tr[u].s[x > tr[u].val];
}
if (u) tr[u].cnt++;
else {
u = ++tot;
tr[u].p = fa;
if (fa) tr[fa].s[x > tr[fa].val] = u; //可能是根节点所以要特判 fa
tr[u].cnt = tr[u].sz = 1;
tr[u].val = x;
}
splay(u, 0); //旋转到根!
}
void build() {
insert(-INF), insert(INF);
}
int pre(int x) { //这里返回的是编号
splay(find(x), 0); //旋转到根
int u = rt;
if (tr[u].val < x) return u; //元素可能不存在,那么就是最后搜到的元素
u = tr[u].s[0];
while (tr[u].s[1]) u = tr[u].s[1];
return u;
}
int nxt(int x) {
splay(find(x), 0);
int u = rt;
if (tr[u].val > x) return u;
u = tr[u].s[1];
while (tr[u].s[0]) u = tr[u].s[0];
return u;
}
void remove(int x) {
int Pre = pre(x), Nxt = nxt(x); //这里一定要先搜索再删除,不然会出事
splay(Pre, 0);
splay(Nxt, rt);
int u = tr[tr[rt].s[1]].s[0];
if (tr[u].cnt > 1) {
tr[u].cnt--;
splay(u, 0);
} else {
tr[tr[rt].s[1]].s[0] = 0;
}
}
int get_rank_by_val(int x) {
splay(find(x), 0);
return tr[tr[rt].s[0]].sz + (tr[rt].val < x) * tr[rt].cnt;
}
int get_val_by_rank(int x) {
int u = rt;
if (tr[rt].sz < x) return INF;
while (15) {
if (tr[tr[u].s[0]].sz >= x) u = tr[u].s[0];
else if (tr[tr[u].s[0]].sz + tr[u].cnt >= x) return tr[u].val;
else x -= tr[tr[u].s[0]].sz + tr[u].cnt, u = tr[u].s[1];
}
}
int main() {
scanf("%d", &n);
build();
while (n--) {
int opt, x; scanf("%d%d", &opt, &x);
if (opt == 1) {
insert(x);
} else if (opt == 2) {
remove(x);
} else if (opt == 3) {
printf("%d\n", get_rank_by_val(x));
} else if (opt == 4) {
printf("%d\n", get_val_by_rank(x + 1));
} else if (opt == 5) {
printf("%d\n", tr[pre(x)].val);
} else {
printf("%d\n", tr[nxt(x)].val);
}
}
return 0;
}
以 AcWing 2437. Splay 为例:
对每个结点记录它区间是否被反转(懒标记,与线段树思路大致相同)。
懒标记下传也和线段树差不多的。
代码中的变量可能与上文不太一样。
#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
int n, m;
struct Node {
int s[2]; //两个儿子
int p; //父节点
int v; //编号
int size, flag; //size是子树大小,flag是是否翻转
void init(int _v, int _p) {
v = _v, p = _p;
size = 1;
}
} tr[N];
int idx, root;
void push_up(int x) {
tr[x].size = tr[tr[x].s[0]].size + tr[tr[x].s[1]].size + 1;
}
void push_down(int x) {
if (tr[x].flag) {
swap(tr[x].s[0], tr[x].s[1]);
tr[tr[x].s[0]].flag ^= 1;
tr[tr[x].s[1]].flag ^= 1;
tr[x].flag = 0;
}
}
void rotate(int x) { //旋转操作
int y = tr[x].p, z = tr[y].p;
bool k = tr[y].s[1] == x; //k=0表示x是y的左儿子,否则是右儿子
tr[z].s[tr[z].s[1] == y] = x, tr[x].p = z;
tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y;
tr[x].s[k ^ 1] = y, tr[y].p = x;
push_up(y); push_up(x);
}
void splay(int x, int k) {
while (tr[x].p != k) {
int y = tr[x].p, z = tr[y].p;
if (z != k)
if ((tr[y].s[1] == x) ^ (tr[z].s[1] == y)) rotate(x);
else rotate(y);
rotate(x);
}
if (!k) root = x;
}
void insert(int v) {
int u = root, p = 0;
while (u) p = u, u = tr[u].s[v > tr[u].v];
u = ++idx;
if (p) tr[p].s[v > tr[p].v] = u;
tr[u].init(v, p);
splay(u, 0); //为了保证时间复杂度是log n,最关键的是每次操作把x旋转到根
}
int get_k(int k) {
int u = root;
while (1) {
push_down(u);
if (tr[tr[u].s[0]].size >= k) u = tr[u].s[0]; //在左子树找
else
if (tr[tr[u].s[0]].size + 1 == k) return u; //在根节点
else k -= tr[tr[u].s[0]].size + 1, u = tr[u].s[1]; //在右子树找
}
return -1;
}
void output(int u) {
push_down(u);
if (tr[u].s[0]) output(tr[u].s[0]); //先遍历左子树
if (tr[u].v >= 1 && tr[u].v <= n) printf("%d ", tr[u].v); //输出这个点
if (tr[u].s[1]) output(tr[u].s[1]); //后遍历右子树
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 0; i <= n + 1; i++) insert(i);
while (m--) {
int l, r;
scanf("%d%d", &l, &r);
l = get_k(l), r = get_k(r + 2);
splay(l, 0), splay(r, l); //旋转
tr[tr[r].s[0]].flag ^= 1;
}
output(root);
return 0;
}


找前驱的代码的p[0]和p[1]应该是s[0]和s[1]吧 QWQ
是 qwq
写错了 awa,不好意思,已修正
%%%
%%%