搜索

剪枝

分组类

把物品分组放在一起。

类型

1. 每组必须要“放满” ，如167. 木棒
2. 每组不一定要“放满”，如165. 小猫爬山，1118. 分成互质组

dfs方式

1. 枚举每一组中放的物品（枚举组合）
2. 枚举每个物品放哪一组 or 新开一组

有种感觉，第一类问题要用解法一，第二类都可以？？

还是不太清楚的感觉，因为我还没有想清楚小猫爬山这题，为什么做法一几乎是做法二的五倍 30ms and 150ms

迭代加深

是用时间换空间的做法，感觉起来类似BFS？

使用场景

1. 有些分支的层数可能极大，并且求出的答案无用且费事
2. 最优解的层数最小。

估价函数优化(IDA*)

用一个估价函数f(<= g(真实步数))使，在当前最大深度下无法求解的分支，直接剪掉。
与 A*类似。

A 与 IDA的选择

当 状态容易表示 状态指数增长较慢 时用 A
当 状态表示很大 状态指数增长较快 时用 IDA
（墨染空大佬的总结）

图论

重在建图!!!

注意

要根据数据范围和要求来看

最后选符合的最便利实现方式。

不一定考什么模型就一定用什么。（如:香甜的黄油）

最短路问题

单源点

1. 边权均非负
   • 朴素版dijkstra（稠密图） $O(n^2)$
   • 堆版dijkstra（稀疏图） $O(mlogn)$
2. 有负权边
   • bellman_ford（SPE：走k次的最短路、判负环） $O(nm)$ （因为负权边要与INF/2比较来判定无法到达）
   • spfa（SPE：判负环）（循环队列可以手写qwq 用的是0 - N-1） $O(km…nm)$

多源点

• flody
  可以有负权边（因为负权边要与INF/2比较来判定无法到达）（不能有负环）

与DP

DP为非拓扑图时转化为最短路问题

多起点或多终点时

考虑用虚拟源点。
虚拟源点就相当于开始时把所有的起点都放入队列。

floyd算法

1. 最短路
2. 传递闭包
3. 找最小环 d[i][j] + g[i][k] + g[k][j]
4. 恰好经过k条边的最短路（倍增）

恰好经过k条边的最短路

1. bellman_ford - $O(nm)$ - 稀疏图
2. 类Floyd的DP + 倍增 - $O(n^3logn)$ - 稠密图

最小生成树

1. prim
   • 朴素版 $O(n^2+m)$ 稠密图
   • 堆版 $O(nlogn + mlogn -> mlogn)$ 与dijkstra相同的优化 基本不用
2. kruskal
   • $O(mlogm)$ 稀疏图

可以用prim的一定可以用kruskal。

注意

若有负权边（即加一条边方案不严格变坏），不能无脑套模板

拓展

1. 生成树和虚拟源点
2. 次小生成树（1. 非严格 2. 严格）
   • 先求最小生成树，再枚举删去最小生成树的边求解。$O(mlogm + nm)$ (Kruskal)
   • 先求最小生成树，再依次枚举非树边，然后将改变加入树中，同时从树中去掉一条边，使最终的图仍是一棵树。$O(m + n^2 + mlogm / mlogn)$（朴素/LCA）

(路径的值是指在最小生成树上的路径)
若求非严格次小生成树，只需要维护两点间的最大路径
若求严格次小生成树，还需要维护两点间的次大路径

负环

常用做法：spfa

1. 统计每个点入队次数，某个点入队n次，说明存在负环（与bellman_ford的判断相同）
2. 统计当前每个点的最短路所包含的边数，若所包含边数>=n，说明存在负环（推荐）

都基于抽屉原理

全都为-1
1 -> 2 -> 3 -> 1
法1：n(n-1) + 1 -> $n^2$
法2：n -> $n$

注意

下方，指图中存在负环！！不一定与起点相连
1. 存在负环要将所有点入队（不一定全部走得到）相当于建立一个虚拟源点0;
2. dist[i] 任意（把所有点放入）

如果是求从某一点出发的负环，即与某一点连通的负环时，dist还是要memset(dist, 0x3f, sizeof dist)。
不然就需要把所有点放入，再判断负环与起点的连通性，就麻烦了。洛谷负环模板

经验

因为时间复杂度看做$O(nm)$

当所有点的入队次数超过2n - 4n …时，我们就认为图中有很大可能是存在负环的。（超时的话，trick的做法）
from yxc

也可以使用stack栈来操作，经验上效果不错。（同样也可以看洛谷那个模板题，有一个点十分久，这两种做法还是看数据，没有绝对的好坏）

差分约束

用最短路：
Xi <= Xj + Ck
x - 自变量，Ck - 常数

用最长路求解：
Xj <= Xi - Ck

最短路-松弛定理 - 不等式组
i -> j
dist[i] <= dist[j] + w

限制是边对点的限制，点能否都走到是无所谓的！！！

转换后若存在负环，即存在Xi < Xi，即无解

应用

1. 求不等式组的可行解
   • 源点需要满足的条件：源点需要能够走到所有的边（这样能都满足松弛定理）
   • 步骤：
     1. 把每个不等式转化为边（Xi <= Xj + Ck）-> （Xj -> Xi 长度为Ck）
     2. 找到一个超级源点，使其可以遍历到所有边
     3. 存源点求一遍单源最短（长）路
        1. 存在负（正）环，无解
        2. 无负（正）环，dist[i]是一个可行解
2. 求最大值和最小值，每个变量的最值
   • 能求的条件：一定是有某个Xi与常数的关系，不然都只是相对关系
   • 结论：
     1. 若求最小值，则求最长路；若求最大值，则求最短路。
   • 转化Xi <= c?
     1. 建立超级源点0，建立0 -> i，长度为c的边
   • 求Xi最大值为例：
     通过链式转换后，一定可以得到 Xi <= 0 + c1 + c2 …，一系列上界，取上界的最小值就是Xi的最小值。（每一个上界是从源点走到Xi的所有方案的权和），即求路径的边长和的最小值

理解

Xi的上界or下界有许多，这些上界or下界就是从虚拟源点出来到达Xi的所有方案的路径总长度，也就是Xi要满足的所有条件，因为全都要满足，所以若求最小值，则求最长路；若求最大值，则求最短路。

注意

一定要去看是否所有的限制条件都被考虑到了。
还有结果是合法的之类的。

最近公共祖先LCA

1. 向上标记法 - O(n)
2. 倍增 - 二进制拼凑 - 预处理 O(nlogn) 查询 O(logn)
   • 定义
     • fa[i][j]表示从i节点开始，向上走$2^j$步能走到的节点。(0 <= j <= [logn])
       j == 0, f[i][j] = fa[i];
       j > 0, fa[i][j] = fa[f[i][j - 1], j - 1];
     • depth[i]表示i节点的深度
     • 哨兵：若从i节点跳$2^j$步会跳过根节点，那么fa[i][j] = 0, depth[0] = 0;（用于判断跳出去的非法状态）
   • 步骤
     1. 先将两个点跳到同一层（若已经是同一个点就直接退出） 枚举k 从大到小
     2. 让两个点同时往上跳，跳到最近公共祖先的下一层（若直接跳到公共祖先的话，不能直接判断它是不是最近的公共祖先） 枚举k 从大到小

3. Tarjan - 离线求LCA - O(n + m)

   • 定义
     • 实质：对向上标记法的优化（运用并查集）
     • 在DFS时，将所有点分为三大类
       1. 2-已经遍历过且回溯过的点（一个节点其对应子树被遍历完的意思）
       2. 1-正在搜索的分支
       3. 0-还未搜索到的点
     • 寻找现在遍历到的点a相关的点b，若这个相关点b已经被遍历过，那么lca(a, b)就是b现在所被合并到当前正在搜索分支上的某个节点。
     • 遍历并回溯了一个点就可以把这个点合并到父节点
     • 遍历完一个再查是为了get_fa(v)是最近公共祖先
       
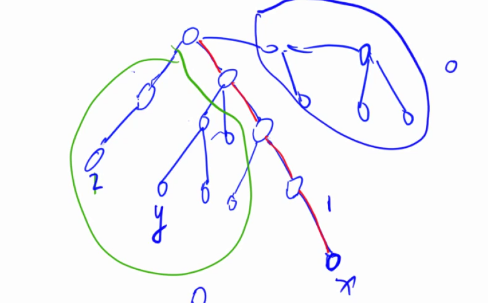
       from 算法提高课

4. RMQ（不常用）预处理 - O(nlogn) 查询 - O(1)

   • 做法
     1. 先求dfs序（回溯也要记一次）
     2. 求lca(x, y)，在dfs序中找到任意一个x和y，找到x和y之间深度最小的节点编号即最小值，也就转化为区间最小值了。

在线 - 问一个答一个
离线 - 全问完了，回答

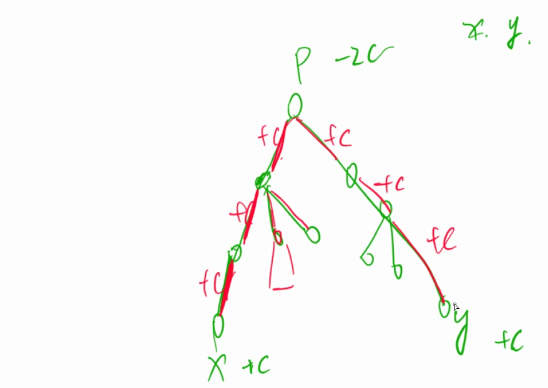
树上差分

x, y, c

d(x) += c
d(y) += c
d(anc) -= c * 2

• 每个点的值就是以这个点为根的子树里的和

对anc以上，x、y以下也没有变化

有向图的强连通分量 O(n + m)

• 概念
  连通分量：u、v可以互相到达
  强连通分量（SCC），即极大连通分量。加入任何点就不是连通分量的 连通分量
  对于一个搜索树，有向边(x, y)（由第一次DFS遍历到的时间节点来编号等得到的时间戳dfn[]）
  树枝边：x是y的父节点（特殊的前向边）
  前向边：x是y的祖先（所有的包括自己的父辈之一）节点
  后向边：y是x的祖先节点（往回搜）
  横叉边：除了以上三种情况的边（dfn[y] < dfn[x]， y已经被搜过了）
  dfn[u]遍历到u的时间戳
  low[u]从u开始走，它所能遍历到的最小的时间戳
  u是其所在强连通分量的最高点，等价于low[u] == dfn[u]
• 判断x是否在SCC中
  1. 存在后向边指向祖先节点
  2. 存在一个横叉边，通过横叉边走到祖先节点

in_stk = true 说明还没有回溯。
（这个我不知道怎么描述，通过代码+图的方式可能好说明）

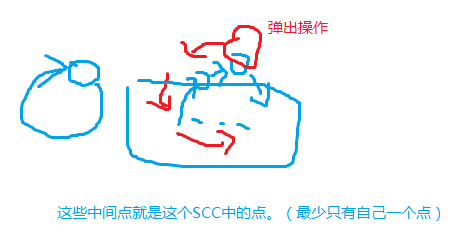
应用

将任意一个有向图通过缩点（将所有的连通分量缩成一个点）的方式转化为有向无环图（DAG、拓扑图）
后用拓扑序递推方式求最短路or最长路

有向图！！！
缩点 重新建图 按拓扑序求解！！！

模板

void tarjan(int u)
{
    dfn[u] = low[u] = timestamp ++;
    stk[++ top] = u, in_stk[u] = true;
    for(int i = h[u]; ~i; i = ne[i])
    {
        int v = ver[i];
        if(!dfn[v]) // 树枝边
        {
            tarjan(v);
            low[u] = min(low[u], low[v]);
        }
        else if(in_stk(v)) // 不是向下的边，横叉边是不需要考虑的，因为是`有向图`，不能够构成一个连通分量
            low[u] = min(low[u], dfn[v]);
    }
    if(dfn[u] == low[u])
    {
        int v;
        ++ scc_cnt;
        do
        {
            v = stk[top --];
            in_stk[v] = false;
            id[v] = scc_cnt;
        } while(u != v);
    }
}

缩点 -> DAG

for(int i = 1; i <= n; i ++)
    for i 所有邻点
        if(i 和 v不在一个SCC)
            add(id(i), id(v)); // 连通块相连（有时不用真的建图，可能只是入读和初度）

注意

SCC编号递减的顺序一定是拓扑序

因为不一定联通， 但每个点都应该要在缩点后的集合内有对应的点

for 所有的点
    if(!dfn[i]) tarjan(i);

tarjan不是能做所以最长路，且对空间复杂度要求较高。

结论

对一个有向图，把它变为scc需要加max(p, q)条边（p出度为0，q入度为0的点的个数）

无向图的双连通分量

• 概念
  对于无向图来说。
  双连通分量，即重连通分量。
  1. 边双连通分量
     把桥这条边删去，整个图不连通
     极大的不包含桥的连通块
     性质：
     1. 不管在内部删掉那条边，图还是连通的
     2. 存在两条没有公共边的路径
  2. 点双连通分量
     割点，把割点删除后这个图不连通
     极大的不包含割点的连通块
     每个割点至少属于两个连通分量
     性质：
     1.
     2.
     两个割点之间的边不一定是桥
     桥的两个端点也不一定是割点
     （两者没啥关系）
     树的边是桥，每个点事边连通分量
     所有的边是点连通分量

边双连通分量

无向图中不存在横叉边

维护dfn，low

1. 如何找到桥

y不能走到x或x的祖宗

dfn[x] < low[y];

1. 如何找到所有的边的双连通分量
   1. 把所有的桥删掉
   2. 用栈 dfn[x] == low[x], x走不回x的父节点

缩点之后是一棵树，边都是桥
度数为1的点至少要加一条边（最少的加边方法就是把两个度数为1的点连一条边）
连了之后导致x，y点分别到根节点的路径都变为不是桥。

点双连通分量

1. 如何求割点
   dfn[x] <= low[y];
   1. 如果x不是根节点，那么x就是割点
   2. x是根节点，至少有两个子节点割点
2. 如何求点双连通分量
   if(dfn[x] <= dfn[y])
   {
   cnt ++;
   if(x != root || cnt > 1) cnt[x] = true;
   将栈中元素弹出弹到y位置为止，且x也属于该点双连通分量（x == y 显然，x < y 弹出后只剩x和y的边，是一个双连通分量）
   }
   开始时要特判若是孤立点也是双联通分量。

缩点之后是一棵树，点是v-dcc
每次都会把会使它自己成为割点的点（那条分支的子节点弹完，也就是弹到v）都弹掉（最后把自己u补上去），这样之后它就不是割点，也就是说存在当前栈中的点（到割点 or 根节点的点）构成一个v-dcc

割点向包含它的v-dcc连条边，只是为了说起来方便，实际上就是直接把割点就放在那个v-dcc中了

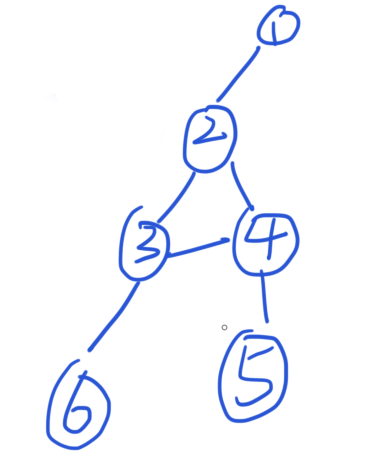
(好用的样例 from ioj)

模板

不经过in_e这条边，无法回到x点或其他祖宗节点

e-dcc

int id[N], dcc_cnt;
bool is_bridge[M];
int indeg[N];

// 要存from 成对变换
void tarjan(int u, int from) // in_e
{
    stk[++ top] = u;
    dfn[u] = low[u] = ++ timestamp;

    for(int i = h[u]; ~i; i = ne[i])
    {
        int v = ver[i];
        if(!dfn[v])
        {
            tarjan(v, i);
            low[u] = min(low[u], low[v]);
            if(dfn[u] < low[v])
                is_bridge[i] = is_bridge[i ^ 1] = true;
        }
        else if(i != (from ^ 1)) // 只要不是往回走的那个边，都可以用来更新（判重边）
            low[u] = min(low[u], dfn[v]);
    }
    if(dfn[u] == low[u]) // 一块
    {
        ++ dcc_cnt;
        int v;
        do
        {
            v = stk[top --];
            id[v] = dcc_cnt;
        } while(u != v);
    }
}

for(int i = 1; i <= n; i ++)
        if(!dfn[i]) tarjan(i, -1);

不经过x点回到祖宗节点，它就不是割点。
（不是根节点的情况下）
所以在dfs过程中，若回溯到这个点它的子节点仍不能访问到x之前的点，它就是割点。
根节点就是它至少有两个子节点。

是否对根节点要特判

v-dcc

求割点

void tarjan(int u)
{
    dfn[u] = low[u] = ++ timestamp;

    int cnt = 0; // 删去u点产生的连通块个数
    for(int i = h[u]; ~i; i = ne[i])
    {
        int v = ver[i];
        if(!dfn[v])
        {
            tarjan(v);
            low[u] = min(low[u], low[v]);
            if(dfn[u] <= low[v]) cnt ++;
        }
        else low[u] = min(low[u], dfn[v]);
    }
    if(u != root && cnt) cnt ++;
}

缩点

int root;
int dcc_cnt;
vector<int> dcc[N];
bool cut[];

void tarjan(int u)
{
    stk[++ top] = u;
    dfn[u] = low[u] = ++ timestamp;

    // 是孤立点
    if(u == root && ~h[u])
    {
        ++ dcc_cnt;
        dcc[dcc_cnt].push_back(u);
        return;
    }

    int cnt = 0;
    for(int i = h[u]; ~i; i = ne[i])
    {
        int v = ver[i];
        if(!dfn[v])
        {
            tarjan(v);
            low[u] = min(low[u], low[v]);
            if(dfn[u] <= low[v])
            {
                cnt ++;
                if(u != root || cnt > 1) cut[u] = true; // 对根节点的特判
                ++ dcc_cnt;
                int y;
                do
                {
                    y = stk[top --];
                    dcc[dcc_cnt].push_back(y);
                } while(v != y);
                dcc[dcc_cnt].push_back(u);
            }
            else low[u] = min(low[u], dfn[v]);
        }
    }
}

遍历每个dcc[i][j] 可以求每个dcc[i]中的cut数

结论

一个无向图，加cnt + 1 >> 2 个边可以使他成为边双连通分量（cnt为缩点后度数为1的点的个数）

二分图

• 概念
  相邻的点是不属于一个集合，特殊的最大流问题
  指无向图
  匈牙利算法（基于深搜）
  匹配：一组边，没有公共点的集合
  最大匹配：边数最多的一组匹配
  匹配点：在匹配中的点
  非匹配点：不在匹配中的点
  增广路径：从一个非匹配点开始走，先走非匹配边再走匹配边最后走到一个非匹配点（左非-> 非 -> 匹 -> … -> 右非） （可以把所有匹配的边去掉变为非匹配的边，增广了）
  最小点覆盖，最大独立集，最小路径点覆盖（最小路径重复点覆盖）
  最小点覆盖，不止是在二分图，而是在一个图中，从中选出最少的点，使得所有的边有一端可以有一个点
  最大独立集，不止是在二分图，选出最多的点，使得选出的点之间（内部）是没有边的。
  推导：在二分图中，等价于出掉最少的点，将所有的边都破坏掉，等价于找最小点覆盖，能把所有的边破坏掉。等价于找最大匹配
  最大团（与最大独立集互补的），选最多的点，使任意边之间有边
  最小路径点覆盖（最小路径覆盖），对一个DAG（有向无环图）来说，用最少的互不相交（点和边都不重复，即点不重复）的路径，将所有点覆盖住
  进行拆点（普通的拆点，1 1’ 2 2’，一个出点，一个入点）,路径 -> 匹配，路径终点 -> 左部非匹配点
  推导：想让求最小路径点覆盖，就是让路径终点最少，左部非匹配点最少，找最大匹配
  最小路径重复点覆盖（和最小路径点覆盖类似，只是没有对重复经过的点的限制）
  做法：求传递闭包（建了许多新边） -> G’, 在G’求最小路径覆盖。
  （最小费用流）最优匹配（给每个边一个权重，达到最大匹配的情况下，最大边权和是多少），KM
  （最大流）多重匹配（每个点可以匹配多个点）

• 结论（在二分图中）
  二分图 == 不存在奇数环 == 染色法不存在矛盾
  最大匹配 == 不存在增广路径
  （二分图中）最大匹配数 == 最小点覆盖 == 总点数 - 最大独立集 == 总点数 - 最小路径覆盖

• 应用
  染色法 - 判定二分图
  一般的二分图做法，匈牙利算法 - 求最大匹配数

注意

染色成二分图的染色方案只需保证两个集合内无边，任意一条边的端点在两个集合内。

虽然是无向图问题，但边可以只建有向边
match[]，可以看做右边连向（匹配到）左边的边

模板

染色法判二分图

• 注意 可能是非联通的

bool dfs(int u, int c, int limit)
{
    color[u] = c;
    for(int i = h[u]; ~i; i = ne[i])
    {
        int v = ver[i];
        if(color[v] == c) return false;
        else if(!color[v])
            if(!dfs(v, 3 - c, limit)) return false;
    }
    return true;
}
bool check(int mid)
{
    memset(color, 0, sizeof color);
    for(int i = 1; i <= n; i ++)
        if(!color[i])
        {
            if(!dfs(i, 1, mid)) return ...;
        }
}

匈牙利算法

int n1, n2;     // n1表示第一个集合中的点数，n2表示第二个集合中的点数
int h[N], e[M], ne[M], idx;     // 邻接表存储所有边，匈牙利算法中只会用到从第一个集合指向第二个集合的边，所以这里只用存一个方向的边
int match[N];       // 存储第二个集合中的每个点当前匹配的第一个集合中的点是哪个
bool st[N];     // 表示第二个集合中的每个点是否已经被遍历过

bool find(int x)
{
    for (int i = h[x]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!st[j])
        {
            st[j] = true;
            if (match[j] == 0 || find(match[j]))
            {
                match[j] = x;
                return true;
            }
        }
    }

    return false;
}

// 求最大匹配数，依次枚举第一个集合中的每个点能否匹配第二个集合中的点
int res = 0;
for (int i = 1; i <= n1; i ++ )
{
    memset(st, false, sizeof st);
    if (find(i)) res ++ ;
}

作者：yxc
链接：https://www.acwing.com/blog/content/405/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

欧拉路径和欧拉回路

• 概念
  欧拉路径，存在一条S到T的路径，不重不漏地经过每条边一次
  欧拉回路，起点和终点是同一个点的欧拉路径

• 结论

  1. 对于无向图来说（所有边都是连通的，点无所谓）
     1. 存在欧拉路径的充分必要条件：度数为奇数的点只能有0或2个。
     2. 存在欧拉路径的充分必要条件：度数为奇数的点只能有0个。
  2. 对于有向图来说（所有边都是连通的，点无所谓）
     1. 存在欧拉路径的充分必要条件：要么所有点的出度均等于入度；要么除了两个点之外，其余所有点的出度等于入度，剩余的两个点：一个满足出度比入度多1（起点），另一个满足入度比出度多1（终点）。
     2. 存在欧拉回路的充分必要条件：所有点的出度均等于入度。
        从S开始DFS，一定会在T结束。（度数都为偶数，进来就要出去

代码

• 得到欧拉路径的倒序，求最小字典序只需要先找点编号小的

所有u的后继节点，都找过了。
欧拉路径从奇数点开始搜，欧拉回路从任意点开始搜。

用边来判重！！！
时间复杂度 - $O(m^2)$

优化用完每一条边就删去，时间复杂度 - $O(n + m)$

无向图，成对变换，反边要标记。

由图可知，这个dfs由于进去然后continue;出来的无意义行为增加时间复杂度
具体题目：1184. 欧拉回路

dfs(u)
{
    for 邻边
        dfs // 扩展
    把u加到序列中
}

inline void dfs(int u)
{
    for(int i = 1; i <= n; i ++)
        if(g[u][i])
        {
            g[u][i] --, g[i][u] --;
            dfs(i);
        }
    ans[++ cnt] = u;
}

int main()
{
    cin >> m;
    while(m --)
    {
        int a, b;
        cin >> a >> b;
        g[a][b] ++, g[b][a] ++;
        deg[a] ++, deg[b] ++;
    }
    int root = 0;
    while(!deg[root]) root ++;
    for(int i = 1; i <= n; i ++)
        if(deg[i] & 1) // 度数为奇数的点
        {
            root = i;
            break;
        }
    dfs(root);
    return 0;
}

拓扑排序

• 概念
  拓扑图，有向无环图。

为保证字典序，优先队列编号

模板

先将所有入度为0的点入队

while(q.size())
{
    t = q[hh ++];
        for t的邻边
            if(-- ind[v] == 0) 放入;

}

高级数据结构

并查集

• 概念
  带权并查集（时间复杂度与k无关）（维护k类），相对思想（相对距离）
  扩展域并查集（O(k)），枚举思想（是第一类…，第二类…）
• 应用
  合并两个集合
  查询某个元素的祖宗节点
• 优化
  路径压缩 - O(logn)
  按秩合并 - O(logn)（深度小的接在大的后面）
  路径压缩 + 按秩合并 - O(alpha(n))
• 扩展
  1. 维护每个集合的大小 -> 绑定在根节点上
  2. 每个点到根节点的距离 -> 绑定在每个元素上（维护“多类”，例食物链）（一般维护当前节点到根的关系）

关于带权并查集与扩展域

树状数组

• 概念
  c[x]，以x结尾的长度为2^k的区间和（k位）

• 应用

  1. 快速求前缀和 - O(logn)
  2. 修改某一个数 - O(logn)
     即区间查询，单点修改

• 扩展

  1. 区间修改，单点查询 - 差分([l, r] + c -> add(l, c), add(r + 1, -c);
  2. 区间修改，区间查询 - 差分 + 公式 (原数组a[]，差分数组b[]。区间修改使用扩展1，区间求和可以转化为：b的前缀和 * (x + 1) - (i * b)的前缀和，通过维护两个前缀和即可)
  3. 也是可以求前缀最大值（加法变为取max（只能满足添加数，不能删除数）

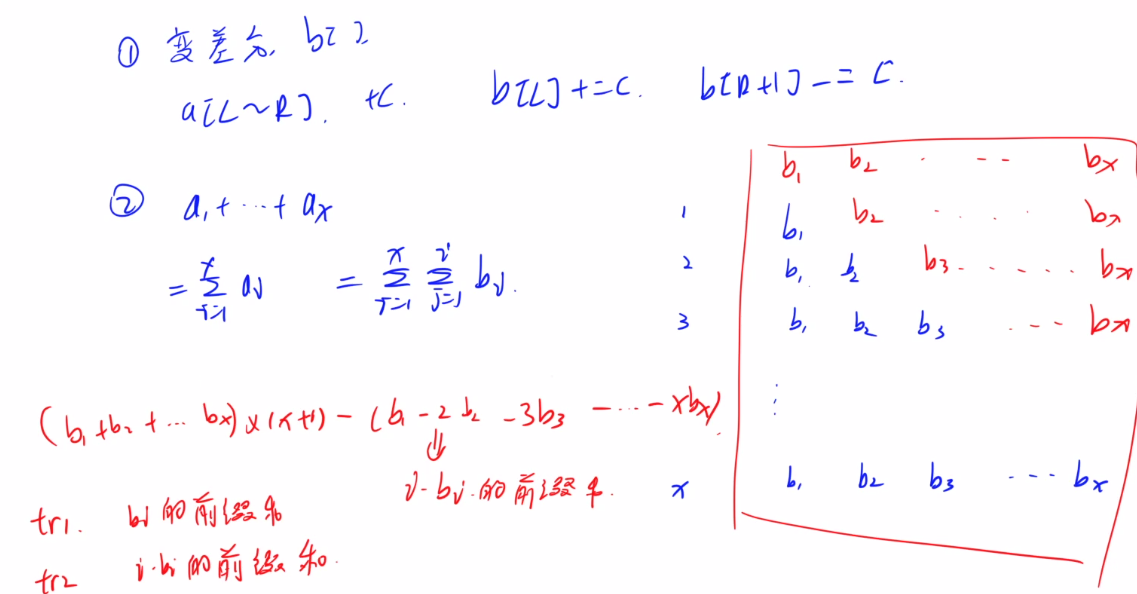
求类逆序对

模板

// 修改
for(int i = x; i <= n; i += lowbit(i)) 
    tr[i] += c;
// 查询
for(int i = x; i; i -= lowbit(i)) 
    res += tr[i];
// 初始化1 - O(nlogn) 常用 + 影响不大
for(int i = 1; i <= n; i ++)
    add(i, a[i]);
// 初始化2 - O(n)
// 法1
for(int x = 1;x <= n;x ++)
    for(int i = x - 1;i >= x - lowbit(x) + 1;i -= lowbit(i)) // 是i >= x - lowbit(x) + 1
         tr[x] += tr[i];
// 法2
// 先求前缀和，然后c[x] = s[x] - s[x - lowbit(x)]

// 若是初始化为1的话，可以之间 tr[i] = lowbit(i);

线段树

• 基本操作
  1. pushup(u)
  2. build()，将一段区间初始化为线段树
  3. modify()，修改
     1. 单点
     2. 区间 - lazydown
  4. query()
• 应用
  懒标记
  扫描线法 （区间修改，区间查询）例
  1. 操作1：将[l, r] + k(-1 or 1)
  2. 操作2：求整个区间中长度>0的区间总长是多少
• 扫描线性质
  1. 永远只考虑根节点的信息（[L, R]）说明query时不会lazydown，也就是不用lazydown
  2. 所有操作是成对出现，且先加后减 - 加tag的地方与减的地方是一样的，不会向下传

求某个区间的某种属性，问的要存下来，还有辅助信息（能不能由两个子区间算出来）。

模板

该模板的子节点区间是[l, mid], [mid + 1, r]

有时query需要维护数据比较多时，可以采取返回结构体的做法，
把updata(Node &u, Node &l, Node &r)

struct Node
{
    int l, r;
    int v;
    int tag; 给当前节点为根的每个节点加上tag。（不包含根节点） // 包不包含要统一
} tr[N * 4];

// 用子节点信息更新父节点信息
updata(Node &u, Node &l, Node &r)
{

}
void push_up(int u)
{
    tr[u].v = max(tr[u << 1].v, tr[u << 1 | 1].v)
}
// 将父节点的懒标记传递下来
void lazy_down(int u) // 查询时把tag传下去，并且清空父节点的tag
{
    if(tr[u].tag)
    {
        left.tag += tr[u].tag, left.sum += (left.r - left.l + 1) * tag;
        right ...
        tr[u].tag = 0;
    }
}
// 建树
void build(int u, int l, int r)
{
    tr[u] = {l, r}; // 不要忘记更新，一定要确定u的区间
    if(l == r) return;
    int mid = l + r >> 1;
    build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
    // push_up()
}
// 修改
void modify(int u, int x, int c) //单点
{
    if(tr[u].l == x && tr[u].r == x) tr[u].v = c;
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;
        if(x <= mid) modify(u << 1, x, c);
        else modify(u << 1 | 1, x, c);
        push_up(u);
    }
}
// 询问
void query(int u, int l, int r)
{
    if(tr[u].l >= l && tr[u].r <= r) return tr[u].v;

    int mid = tr[u].l + tr[u].r >> 1;
    int v = 0;
    if(l <= mid) v = query(u << 1, l, r);
    if(r > mid) v = max(v, query(u << 1 | 1, l, r);

    return v;
}

可持续化数据结构

• 可持久化的前提: 本身的拓扑结构不变
  解决的问题: 历史记录, 可以存下来数据结构的所有历史版本
  只记录当前版本与前一个版本不同的节点

trie的可持久化

线段树的可持久化 - 主席树

平衡树 - Treap

AC自动机

树链剖分

Blog1
Blog2
Blog3
Blog4

数学知识

质数相关

试除法求素数

bool is_prime(int x)
{
    if(x < 2) return false;
    for(int i = 2; i <= x/i; i ++)
        if(x % i == 0) return false;
    return true;
}

分解质因数

void div(int x)
{
    for(int i = 2; i <= x/i; i ++)
        if(x % i == 0)
        {
            int cnt = 0;
            while(x % i == 0)
            {
                x /= i;
                cnt ++;
            }
            printf("%d %d\n", i, cnt);
        }
    if(x > 1) printf("%d %d\n", x, 1);
}

筛选法求素数

朴素筛法 $O(nlogn)$ (所有数向上筛)

void get_primes(int x)
{
    for(int i = 2; i <= x; i ++)
    {
        if(!st[i]) prime[cnt ++] = i;
        for(int j = i + i; j <= x; j += i)
            st[j] = true;
    }
}

埃氏筛法 $O(nloglogn)$ (质数向上筛)

void get_primes(int x)
{
    for(int i = 2; i <= x; i ++)
        if(!st[i])
        {
            prime[cnt ++] = i;
            for(int j = i + i; j <= x; j += i)
                st[j] = true;
        }
}

线性筛素数 $O(n)$ (最小质因子筛)

void get_primes(int x)
{
    for(int i = 2; i <= x; i ++)
    {
        if(!st[i]) prime[cnt ++] = i;
        for(int j = 0; prime[j] <= x / i; j ++) //（不用cnt 质数 == 时break 合数 到i的最小质因子break）
        {
            st[prime[j] * i] = true;
            if(i % prime[j] == 0) break;
        }
    }
}

约数(因子)相关

试除法求约数(因子) $O(sqrt(n))$

vector<int> get_divisors(int n)
{
    vector<int> res;
    for(int i = 1; i <= n/i; i ++)
        if(n % i == 0)
        {
            res.push_back(i);
            if(n/i != i) res.push_back(n/i);
        }
    sort(res.begin(), res.end());
    return res;
}

约数(因子)个数

n = p1^a1 * p2^a2 ... * pk^ak.
ans = (a1+1)*(a2+1)...*(ak+1); // 本质上把所有质因子存在个数从[0, a]都弄了一遍

约数(因子)之和

n = p1^a1 * p2^a2 ... * pk^ak.
ans = (p1^0+p1^1+...+p1^a1)*(pk^0+pk^1+...+pk^ak); //拆开括号,就是上面的所有组合了,加起来就是它们的和了

最大公约数

int gcd(int a, int b)
{
    // if(a % b == 0) return b;
    // return gcd(b, a % b);
    return b ? gcd(b, a % b) : a;
}

欧拉函数相关

公式法求欧拉函数

// n = p1^a1 * p2^a2 ... * pk^ak.
// res = n*(1-1/a1)*(1-1/a2)...(1-1/ak);
// res = n /a1*(a1-1)*...;  为了避免出现小数
cin >> a;
int res = a;
for(int i = 2; i <= a/i; i ++)
{
    if(a % i == 0)
    {
      res = res / i * (i - 1);
      while(a % i == 0) a /= i;
    }
}
if(a > 1) res = res / a * (a - 1);

筛法求欧拉函数

inline void get_eulers()
{
  phi[1] = 1;
  for(int i = 2; i <= n; i ++)
  {
    if(!st[i])
    {
      primes[cnt ++] = i;
      phi[i] = i - 1;
    }
    for(int j = 0; primes[j] <= n / i; j ++)
    {
      int t = primes[j] * i;
      st[t] = true;
      if(i % primes[j] == 0)
      {
        phi[t] = phi[i] * primes[j];
        break;
      }
      phi[t] = phi[i] * (primes[j] - 1);
    }
  }
}

快速幂相关

快速幂模板

// 有时中途要转LL
int qpm(int a, int b, int p)
{
    int ans = 1 % p, t = a;
    while(b)
    {
        if(b & 1) ans = (LL)ans * t % p;
        t = (LL)t * t % p;
        b >>= 1;
    }
    return ans;
}

快速幂求逆元(与欧拉定理$O(nsqrt(n))$or费马小定理结合$O(nlogn)$)

乘法逆元的定义
若整数 b，m 互质，并且对于任意的整数 a，如果满足 b|a，则存在一个整数 x，使得 a/b≡a×x(modm)，则称 x 为 b 的模 m 乘法逆元，记为 b−1(modm)。
b 存在乘法逆元的充要条件是 b 与模数 m 互质。当模数 m 为质数时，bm−2 即为 b 的乘法逆元。

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>

using namespace std;

typedef long long LL;

inline int qpm(int a, int b, int c)
{
  int ans = 1 % c;
  while(b)
  {
    if(b & 1) ans = (LL)ans * a % c;
    a = (LL)a * a % c;
    b >>= 1;
  }
  return ans;
}

int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    int T; cin >> T;
    while(T --)
    {
      int a, p;
      cin >> a >> p;
      if(a % p == 0) cout << "impossible" << endl; // 0 不存在逆元
      else cout << qpm(a, p-2, p) << endl; // 不能判qpm()的值不为0 因为 p=2的时候 2, 2, 是1
    }

    return 0;
}

ex_gcd相关

裴蜀定理:
  对于任意正整数a,b, 一定存在(非零?)整数x, y使得 ax + by = gcd(a, b)

因为我们已知下一层的结果, 即:bx+(a%b)y = d
可化为 bx+(a-a/b*b)y = d
整理得 ay + b(x-a/b*y) = d
这里的ay的y是现在这一层的x, 这里的(x-a/b*y)是现在这一层的y
所以有t = x, x = y, y = t-a/b*y

inline void ex_gcd(int a, int b, int &x, int &y)
{
  if(!b)
  {
    x = 1, y = 0;
    return;
  }
  ex_gcd(b, a % b, x, y);
  int t = x;
  x = y, y = t-a/b*y;
}

int main()
{
  int a, b, x, y;
  cin >> a >> b;
  ex_gcd(a, b, x, y);
  cout << x << ' ' << y << endl;
  return 0;
}

解线性同余方程

ax = c(mod b),即 ax+by=c
方程有解当且仅当gcd(a,b)|c
通解, x = x0 - b/d, y = y0 + a/d
a(x0-b/d)+b(y0+a/d) = d
所以求最小的非负x的解, 就是x = (x%b+b)%b

注意 解出的x是ax+by=d的解,而非ax+by=c的解,注意要乘上c/d才行.
然后解出的解一定可以控制在[0, b-1]之间的(最小的)
(注意转LL)
下面这题不用保证正负
inline int ex_gcd(int a, int b, int &x, int &y)
{
  if(!b)
  {
    x = 1, y = 0;
    return a;
  }
  int d = ex_gcd(b, a % b, x, y);
  int t = x;
  x = y, y = t-a/b*y;
  return d;
}

int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    int T; cin >> T;
    while(T --)
    {
      int a, b, c, d, x, y;
      cin >> a >> c >> b;
      d = ex_gcd(a, b, x, y);
      if(c % d == 0) cout << (LL)x*c/d % b << endl;
      else cout << "impossible" << endl;
    }
    return 0;
}

中国剩余定理(crt)相关

m1, m2, … mk两两互质
M = m1m2…mk
Mi = M/mi 与 mi互质, 可得Mi的逆
构造通解: x = a1*M1*M1$^{-1}$+a2*M2*M2$^{-1}$+…+ak*Mk*Mk$^{-1}$

LL n, x, y;
LL A = 1;
LL a1[N], a2[N], b[N];

void ex_gcd(LL a, LL b, LL &x, LL &y)
{
    if(!b)
    {
        x = 1, y = 0; // 0 -> d - 1
        return;
    }
    ex_gcd(b, a % b, x, y);
    LL t = x;
    x = y, y = t - a / b * y;
    return;
}

int main()
{
    cin >> n;
    for(int i = 1; i <= n; i ++)
    {
        cin >> a1[i] >> b[i];
        A *= a1[i];
    }
    for(int i = 1; i <= n; i ++) a2[i] = A / a1[i]; // Mi
    LL res = 0;
    for(int i = 1; i <= n; i ++)
    {
        ex_gcd(a2[i], a1[i], x, y);
        res = res + b[i] * a2[i] * ((x % a1[i] + a1[i]) % a1[i]);
    }
    cout << res % A << endl;

扩展中国剩余定理(ex_crt)

若m1, m2 … mk之间不一定互质

自己写的推导第一版

自己写的推导第二版

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>

using namespace std;

typedef long long LL;

const int N = 1e5 + 10;

int n;
LL r[N], m[N];

LL mod(LL a, LL b)
{
  return (a%b+b)%b;
}
LL qmul(LL a, LL b, LL P)
{
    LL ans = 0;
    while(b)
    {
        if(b & 1) ans = (ans + a) % P;
        a = a * 2 % P;
        b >>= 1;
    }
    return ans;
}
LL ex_gcd(LL a, LL b, LL &x, LL &y)
{
    if(!b)
    {
        x = 1, y = 0;
        return a;
    }
    LL d = ex_gcd(b, a % b, x, y);
    LL t = x;
    x = y, y = t - a / b * y;
    return d;
}
LL ex_crt()
{
    LL A, B, C, d, x, y, R, M; // R - 余数，答案, M - lcm(m1 ... mn)
    M = m[1], R = r[1];
    for(int i = 2; i <= n; i ++)
    {
        A = M, B = m[i], C = (r[i] - R % B + B) % B; // 防溢出
        d = ex_gcd(A, B, x, y); // 求出 == d时的x
        if(C % d != 0) return -1; // 无解

        x = mod(qmul(x, C/d, B/d), B/d); // 更新为 == C的x答案同时保证最小非负整数(其实可以不用, 只要取mod变小就好了)
        // x = x * C/d % (B/d); // 更新为 == C的x答案
    // x = mod(x*C/d, B/d); 保证最小非负整数(其实可以不用, 只要取mod变小就好了)
        R += x * M; // 更新R
        M *= B/d; // 更新M, 乘倍数即可 
        R = (R % M + M) % M;
    }
    return (R % M + M) % M;
}

int main()
{
    scanf("%d", &n);
    for(int i = 1; i <= n; i ++) scanf("%lld%lld", &m[i], &r[i]);

    printf("%lld\n", ex_crt());

    return 0;
}
/*
x = R(mod M)
x = ri(mod mi)
*/
/*
ax = r(mod m[i])
*/

高斯消元相关

一般能够在$O(n^3)$的时间复杂度内,求解包含n个方程, n个未知数的,多元线性方程组.

解有三种情况:无解, 无穷多组解, 唯一解.

输入的是n(n+1)的矩阵(系数nn, n是常数)
行列变换操作:
初等行列变换
1. 把某一行乘一个非零的数
2. 交换某2行
3. 把某行的若干倍加到另一行上去

// -> 上三角形式
a11*x1+.....+a1n*xn=b1
    a22*x2+...a2nxn=bn
                 ...
                 xn=bn

解所对应的情况
1. 完美阶梯型 -> 唯一解
2. 0 = 非零(矛盾) -> 无解
3. 0 = 0(有方程可以被别的表示出来) -> 无穷多组解

算法步骤:

1. 找到当前列绝对值最大且还没有处理的一行(为了处理好精度问题)
2. 将该行换到(当前)最上面去
3. 将该行第一个数变为1
4. 将下面所有行的当前列削成0

模板

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <cmath>

using namespace std;

const int N = 110;
const double eps = 1e-6;

int n;
double a[N][N];

inline int gauss()
{
  int c, r;
  for(c = r = 0; c < n; c ++) // c->列, r->行
  {
    int t = r;
    for(int i = r; i < n; i ++) // find max_fabs
      if(fabs(a[i][c]) > fabs(a[t][c]))
        t = i;
    if(fabs(a[t][c]) < eps) continue; // about Xc none
    for(int i = c; i < n+1; i ++) swap(a[t][i], a[r][i]); // max->top
    for(int i = n; i >= c; i --) a[r][i] /= a[r][c]; // 化1-从后往前
    for(int i = r+1; i < n; i ++) // 其他化0
      if(fabs(a[i][c]) > eps) // 不为0才需要化
        for(int j = n; j >= c; j --) // 从后往前
          a[i][j] -= a[i][c] * a[r][j];
    r ++;
  }
  if(r < n) // 有x没有解出
  {
    for(int i = r; i < n; i ++) // r~n-1 左边为0, 右边是否为0
      if(fabs(a[i][n]) > eps) return 0; // 0 = 非0 无解
    return 2; // 0 = 0 无数个解
  }
  for(int i = n-1; i >= 0; i --) // 求解每个x
    for(int j = i+1; j < n; j ++)
      a[i][n] -= a[i][j]*a[j][n]; // 不为0才需要消(要乘系数)
  return 1; // 唯一解
}

int main()
{
  cin >> n;
  for(int i = 0; i < n; i ++)
    for(int j = 0; j < n+1; j ++)
      cin >> a[i][j];
  int res = gauss();
  if(res == 1)
  {
    for(int i = 0; i < n; i ++)
      printf("%.2lf\n", a[i][n]);
  }
  else if(res == 0) puts("No solution");
  else puts("Infinite group solutions");

  return 0;
}

高斯消元解异或线性方程组

过程一致
^看作不进位的2进制加法

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <cmath>

using namespace std;

const int N = 110;

int n;
int a[N][N];

inline int gauss()
{
  int c, r;
  for(c = r = 0; c < n; c ++) // c->列, r->行
  {
    int t = r;
    for(int i = r; i < n; i ++) // find max_fabs
      if(a[i][c])
      {
        t = i;
        break;
      }
    if(!a[t][c]) continue; // about Xc none
    for(int i = c; i < n+1; i ++) swap(a[t][i], a[r][i]); // max->top
    // for(int i = n; i >= c; i --) a[r][i] /= a[r][c]; // 化1-从后往前
    for(int i = r+1; i < n; i ++) // 其他化0
      if(a[i][c]) // 不为0才需要化
        for(int j = n; j >= c; j --) // 从后往前(异或无所谓)
          a[i][j] ^= a[r][j];
    r ++;
  }
  if(r < n) // 有x没有解出
  {
    for(int i = r; i < n; i ++) // r~n-1 左边为0, 右边是否为0
      if(a[i][n]) return 0; // 0 = 非0 无解
    return 2; // 0 = 0 无数个解
  }
  for(int i = n-1; i >= 0; i --) // 求解每个x
    for(int j = i+1; j < n; j ++)
      a[i][n] ^= a[i][j]*a[j][n]; // 不为0才需要消(要乘系数)
  return 1; // 唯一解
}

int main()
{
  cin >> n;
  for(int i = 0; i < n; i ++)
    for(int j = 0; j < n+1; j ++)
      cin >> a[i][j];
  int res = gauss();
  if(res == 1)
  {
    for(int i = 0; i < n; i ++)
      printf("%d\n", a[i][n]);
  }
  else if(res == 0) puts("No solution");
  else puts("Multiple sets of solutions");

  return 0;
}

组合数相关

根据题目选择求解方式

${b \choose a}$

预处理-递推-$O(nm)$-组合数1

for(int i = 0; i < N; i ++)
    for(int j = 0; j <= i; j ++)
      if(!j) c[i][j] = 1;
      else c[i][j] = c[i-1][j]+c[i-1][j-1];
输出: c[a][b]

预处理-快速幂+逆元-$O(nlogn)$-组合数2

模数要是质数

inline void prev_calu()
{
  fact[0] = infact[0] = 1;
  for(int i = 1; i < N; i ++)
  {
    fact[i] = (LL)fact[i-1]*i%P;
    infact[i] = (LL)infact[i-1]*qpm(i, P-2, P)%P;
  }
}
输出: (LL)fact[a]*infact[b]%P*infact[a-b]%P

Lucas定理-$O(p*logplog_pn)$ -> $O(plognlogp)$-组合数3

${b \choose a} \equiv {b\mod{p} \choose a\mod{p}} * {b/p \choose a/p} \pmod{p}$

$a = a_kp^k+a_{k-1}p^{k-1}+…+a_0p^0$
$b = b_kp^k+b_{k-1}p^{k-1}+…+b_0p^0$

$(1+x)^p = {0 \choose p}x^0+{1 \choose p}x^1+…+{p \choose p}x^p \equiv 1+x^p \pmod{p}$

(累死了直接贴两个blog吧)
Lucas定理证明
卢卡斯定理（十分钟带你看懂）

int qpm(int a, int b)
{
  int ans = 1 % p;
  while(b)
  {
    if(b & 1) ans = (LL)ans * a % p;
    a = (LL)a * a % p;
    b >>= 1;
  }
  return ans;
}
int C(int a, int b)
{
  int res = 1;
  for(int i = 1, j = a; i <= b; i ++, j --)
  {
    res = (LL)res * j % p;
    res = (LL)res * qpm(i, p-2) % p;
  }
  return res;
}
int lucas(LL a, LL b)
{
  if(a < p && b < p) return C(a, b);
  return (LL)C(a%p, b%p) * lucas(a/p, b/p) % p;
}

输入: a, b, p(p为质数)
输出: lucas(a, b)

从定义出发-组合数4

化简高精度 -> 只写高精乘
分解质因数 $= p_1^{a_1}p_2^{a_2}…p_k^{a_k}$
$a! = \lfloor \frac{a}{p} \rfloor + \lfloor \frac{a}{p^2} \rfloor + …$ 得到a!的p的次数
步骤
1. 筛素数(1~5000)
2. 求每个质数的次数(求a!中p的次数)
3. 高精度乘法

考虑质数的次数的思路很妙!!!

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <vector>

using namespace std;

const int N = 5010;

int cnt;
int primes[N], sum[N];
bool st[N];
vector<int> tc;

inline void get_primes(int n)
{
  for(int i = 2; i <= n; i ++)
  {
    if(!st[i]) primes[cnt ++] = i;
    for(int j = 0; primes[j] <= n/i; j ++)
    {
      st[primes[j]*i] = true;
      if(i % primes[j] == 0) break;
    }
  }
}
inline int get(int n, int p)
{
  int res = 0;
  while(n)
  {
    res += n/p;
    n /= p;
  }
  return res;
}
inline vector<int> mul(vector<int> a, int b)
{
  tc.clear();
  int t = 0;
  for(int i = 0; i < a.size(); i ++)
  {
    t += a[i] * b;
    tc.push_back(t % 10);
    t /= 10;
  }
  while(t) tc.push_back(t % 10), t /= 10;
  return tc;
}

int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    int a, b;
    cin >> a >> b;
    get_primes(a);

    for(int i = 0; i < cnt; i ++)
    {
      int p = primes[i];
      sum[i] = get(a, p) - get(b, p) - get(a-b, p);
    }
    vector<int> res;
    res.push_back(1); // init(); !!
    for(int i = 0; i < cnt; i ++)
      for(int j = 0; j < sum[i]; j ++)
        res = mul(res, primes[i]);
    for(int i = res.size()-1; i >= 0; i --)
      cout << res[i];
  cout << endl;
    return 0;
}

Catalan(卡特兰数)

1. 公式法: $f[n] = \frac{{n \choose 2n}}{n+1}$
2. 递推式: $f[n] = f[n-1]f[0]+f[1]f[n-2]+…+f[0][n-1]$ $f[0] = f[1] = 1$

容斥原理相关

韦恩图做示例:
3个互相相交圆的总面积为: $S1+S2+S3-S1\cap S2-S2\cap S3-S1\cap S3+S1\cap S2\cap S3$
推广:
n个圆, (+)1-2+3-4+…(或者说集合与元素个数)

感觉主要是种思想
可以优化暴力
能被整除的数
$O(nm) -> O(m2^m)$

博弈论相关

• 公平组合游戏ICG:
  1. 两名玩家交替行动
  2. 在游戏的任意时刻,玩家可以进行的合法操作与轮到哪名玩家无关
  3. 不能行动的玩家判负

必胜状态:处必胜状态有某种操作使它到达的状态是必败状态.
必败状态:所有能到的状态都是必胜状态.

Nim游戏

Nim属于公平组合游戏

• 结论:

  1. $a_1\^a_2\^…\^a_n = 0$ 先手必败
  2. $a_1\^a_2\^…\^a_n \neq 0$ 先手必胜

• $0\^0\^…\^0 = 0$ (终值状态)

• $a_1\^a_2\^…\^a_n = x = \neq 0$

x的二进制表示中最高的一位1在第k为, a1~an中必然存在一个数ai, ai的第k位是1

在=x的情况下, 一定存在一种取法使得… = 0 :
ai ^ x < ai
ai - (ai ^ x) > 0
ai - (ai - ai ^ x) = ai ^ x -> (…) ^ x = x ^ x = 0
在=0的情况下, 一定不存在一种取法使得… = 0 :
ai ^ … = 0
ai’ ^ … = 0
两式异或, 得ai ^ ai’ = 0 -> ai = ai’ 与 ai’ < ai矛盾

初始状态 ^… 为多少最后也就为多少.

裸的版本

变种

1. 变种1

SG函数

• 概念
  Mex运算:在S(一个非负整数集合)中找到不属于这个集合的自然数. {1, 2, 3} -> {0}
  SG函数:
  SG(终点) = 0; SG(x) = mex{SG(y1), …, SG(yk)} // yi 为 x能到的状态
  SG(x) = 0 - 必败(不能到0) SG(x) != 0 - 必胜(可以到0)
  多个图, $SG(x_1)\^SG(x_2)…\^SG(x_n) = 0$必败, !=0 必胜
  由SG函数理论，多个独立局面的SG值，等于这些局面SG值的异或和(sg(x) = Mex{sg(yi))}
  注意:vis的取值, 为???
  明确sg的值为不属于sg所能达的所有状态的最小自然数(通过必胜点和必败点理解)

sg的范围是看询问的数值大小, vis是看选择方案的多少
vis数组要为每个sg函数独自开, 要开在里面

sg不定义为0/1而是要定义成这么复杂的东西的原因是可能存在很多个游戏(我可以选择任何一个图来把一个状态变成另一个状态)
多个图可以直接异或sg

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>

using namespace std;

const int N = 110, M = 1e4 + 10;

int n, m;
int a[N], f[M];

inline int sg(int x)
{
  if(f[x] != -1) return f[x];
  bool vis[N];
  memset(vis, 0, sizeof vis);
  for(int i = 0; i < m; i ++)
    if(x >= a[i]) vis[sg(x-a[i])] = true;
  for(int i = 0; i < N; i ++)
    if(!vis[i]) return f[x] = i;
}

int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    memset(f, -1, sizeof f);
    cin >> m;
    for(int i = 0; i < m; i ++) cin >> a[i];
    cin >> n;
    int res = 0;
    for(int i = 0; i < n; i ++)
    {
      int x;
      cin >> x;
      res ^= sg(x);
    }
    if(res) cout << "Yes" << endl;
    else cout << "No" << endl;
    return 0;
}