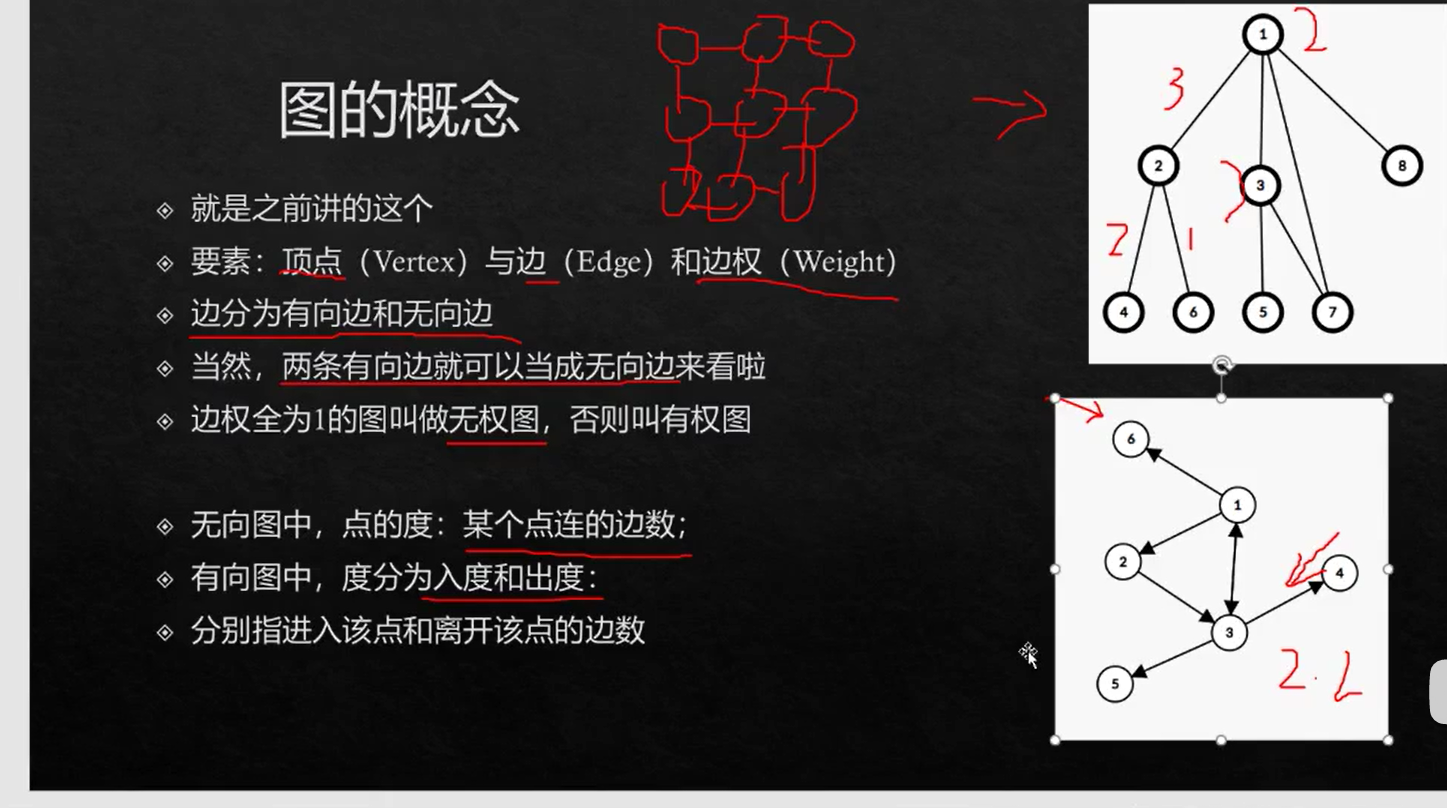
图的概念：

入度: 进入该点的边数

扑拓排序

应用：用来判断有向图中是否有环

该右图中： 0 和 1的入度都为 0 <起始点>
先让 0，1 入队，其它 <2,4,5> 入度都减小 1
2 本来入度为 1，现在减到 0，故让 2 入度；

算法思路：

算法思路：
1）统计图中每个节点的入度 用in[i]数组
2）借助一个队列 queue，将所有入度为0的节点入队。
3）当queue非空时，依次将队首节点出队，依次将队首节点的所有邻接节点 in[v] 的入度-1
//你删掉一个入度为0的点，那么和它相连的点入度也相应减少 1
4）是有向无环图，则所有节点一定都入队并出队过
用个cnt 计数器

模板题目：
拓扑排序·一 HihoCoder - 1174

#include <bits/stdc++.h>
using namespace std;
const int mod=142857;
const int N=1e5+10;
int n,m,cnt,x,in[N];
vector <int > E[N];
queue <int > q; 

void init(){
    for(int i=1;i<=n;i++)
        in[i] = 0,E[i].clear();
    cnt=0; 
} 

bool topsort(){
    for(int i=1;i<=n;i++)//这里是n 
        if(!in[i]) q.push(i);
    while(!q.empty()){
        int now=q.front();
        q.pop();cnt++;
        for(int i=0;i<E[now].size();i++){// 遍历由某点指向的所有点E[1][0]=4;E[1][1]=5;
            int v=E[now][i];
            if(--in[v]==0) q.push(v);
        }
    }//是否为有向无环图 入队次数是否等于顶点数 
    return cnt==n;
}

int main(){
    int t;
    scanf("%d",&t);
    while(t--){
        int x,y;
        cin>>n>>m;
        init();
        while(m--){
            scanf("%d %d",&x,&y);
            E[x].push_back(y);  //E[1]=2
            in[y]++;
        }
        if(topsort()) puts("Correct");
        else puts("Wrong");
    }


    return 0;
}

确定比赛名次

补充 队列queue相关知识：

front() 获取队首
back() 获取队尾
pop() 队首元素出队
empty()：如果 queue 中没有元素的话，返回 true
注意：在使用pop()之前，一定要使用empty()判断是否为空

补充 vector容器相关知识：

C++ 中vector的使用方法
C++ 中vector的使用方法

push_back 在数组的最后添加一个数据
pop_back 去掉数组的最后一个数据
erase 删除指针指向的数据项
clear 清空当前的vector

（vector<int>test;//建立一个vector
test.push_back(1);
test.push_back(2);//把1和2压入vector，这样test[0]就是1,test[1]就是2 ）

使用迭代器访问元素:

vector<int>::iterator it;
for(it=vec.begin();it!=vec.end();it++)
    cout<<*it<<endl;