最短路径问题复习
本帖通过将自己写的几篇题解发送给 CHATGPT4.0 进行总结生成的方式得到内容
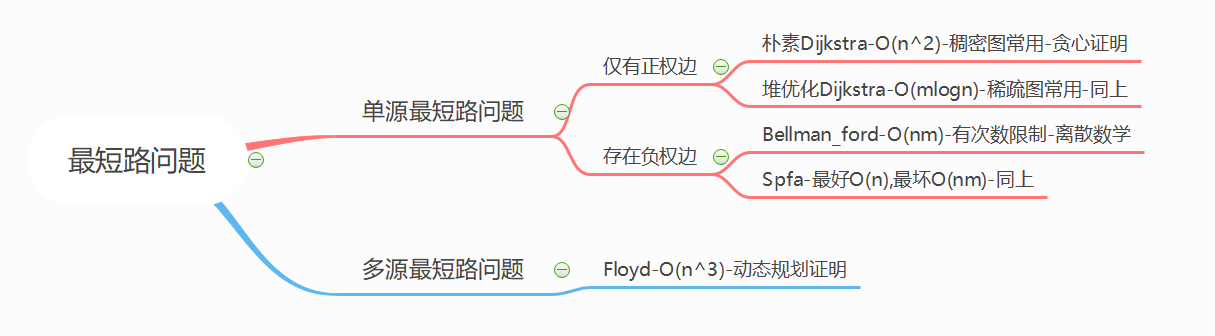
这是对几种常见最短路径算法的总结和分析:
1. Dijkstra算法
Dijkstra算法适用于处理带权图中的单源最短路径问题,且所有边的权重都必须为非负值。它采用贪心策略,通过维护一个距离数组dist[]来记录从源点到每个顶点的最短距离,以及一个状态数组state[]来标记每个顶点的最短路径是否已确定。
核心思路:
- 初始化
dist[],源点为0,其他为无穷大。 - 重复以下步骤,直到所有顶点的最短路径都被确定:
- 选择一个未确定最短路径的顶点,其到源点的距离最短。
- 更新该顶点可达的所有未确定顶点的距离。
优化:使用优先队列(小根堆)来快速选择当前未确定顶点中距离最短的顶点,优化了从dist数组中选择最小值的过程。
2. Bellman-Ford算法
Bellman-Ford算法可以处理图中包含负权边的单源最短路径问题。它通过对所有边重复进行松弛操作,逐步减小源点到各顶点的估计距离,直到这些估计距离达到最短路径的真实距离。
核心思路:
- 初始化:源点到自身距离为0,到其他顶点为无穷大。
- 对所有边进行
n-1次遍历,每次尝试通过每条边进行松弛操作。 - 检查负权环:再进行一次所有边的松弛,如果还能松弛成功,则存在负权环。
3. SPFA算法
SPFA算法是Bellman-Ford算法的一种改进,适用于处理负权边。它通过一个队列来优化松弛过程,只对那些在上一轮松弛中距离被更新过的顶点的邻接顶点进行新一轮的松弛。
核心思路:
- 初始化:源点入队。
- 队列不空时,处理队列中的顶点,对其所有邻接点尝试进行松弛操作。
- 如果邻接点的距离被更新且未在队列中,则将其入队。
4. Floyd算法
Floyd算法处理的是所有顶点对的最短路径问题,它是一个典型的动态规划算法。适用于任意两点间的最短路径计算,能处理负权边,但不适合含有负权环的图。
核心思路:
- 初始化距离矩阵
dist[][],直接相连的点设置为边权重,不直接相连的设置为无穷大,自身为0。 - 使用三重循环,通过尝试每个顶点作为中介点来更新其他所有顶点对的距离。
这些算法各有优势和适用场景,选择合适的算法依据具体问题的需求和图的特性(如边权性质、图的稠密程度等)。

