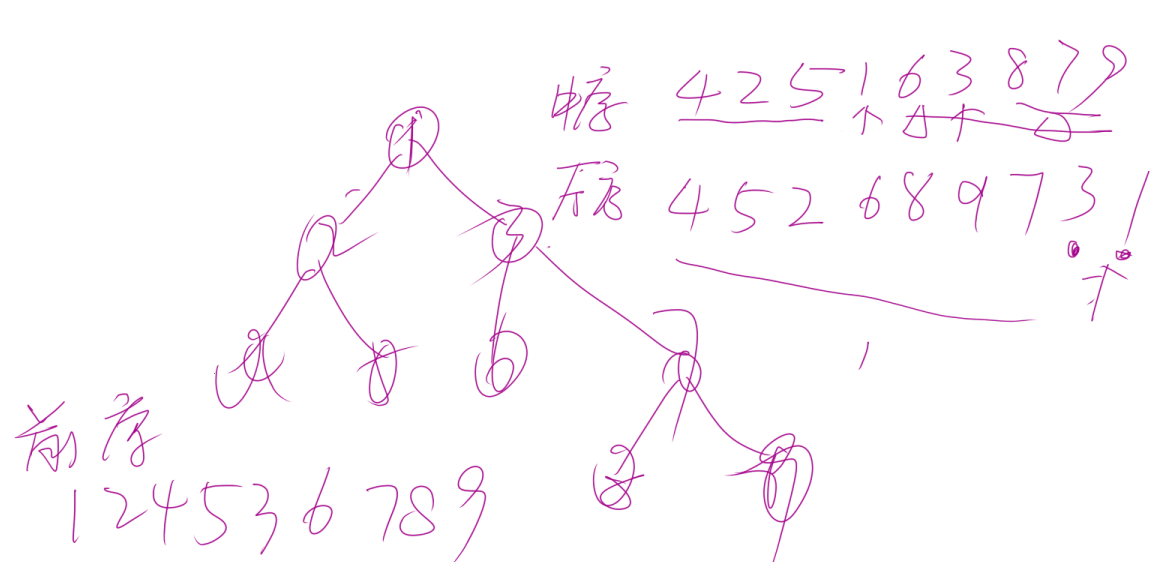
思路

已知2种遍历方法，先构造出来二叉树，再用遍历函数遍历即可。
一次构造并打印需要的遍历，难度较高，不如分拆简单。

后序遍历从后往前遍历，“根右左”的顺序

2个不同的root

在build函数中，第一个root是从post或pre中获得。第2个root是作为返回值的root。这2个root的区别是，第1个root是第2个root的父节点。

已知中序，前序构造二叉树，输出后序

#include <cstdio>
#include <map>
using namespace std;
const int N=1e6+10;
int pre[N],in[N],n;
int l[N],r[N],p=1;
map<int,int> mp;
void post(int root){
    if(!root) return;
    if(l[root]) post(l[root]);
    if(r[root]) post(r[root]);
    printf("%d",root);
}
int build(int left,int right){
    if(left>right) return 0;
    int root=pre[p++];//第1个root
    int i=mp[root];
    l[root]=build(left,i-1);
    r[root]=build(i+1,right);
    return root;//第2个root作为第1个root的子节点返回
}
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++){//中序
        scanf("%d",&in[i]);
    }
    for(int i=1;i<=n;i++){//前序
        scanf("%d",&pre[i]);
    }
    for(int i=1;i<=n;i++){//映射
        mp[in[i]]=i;
    }
    build(1,n);//构造
    post(1);//后序打印
    return 0;
}

已知中序，后序构造二叉树，输出前序

#include <cstdio>
#include <map>
using namespace std;
const int N=1e6+10;
int in[N],post[N],n;//存入中序，前序
int l[N],r[N],p;//构造二叉树
map<int,int> mp;
void pre(int root){//前序遍历
    if(root==0) return;
    printf("%d",root);
    if(l[root]!=0) pre(l[root]);
    if(r[root]!=0) pre(r[root]);
}
//构造出二叉树，再用pre输出一遍
int build(int left,int right){
    if(left>right) return 0;
    int root=post[p];
    int i=mp[root];
    p--;
    //递归的目的是把当前root放到正确的位置上
    r[root]=build(i+1,right);
    l[root]=build(left,i-1);
    return root;
}
int main(){
    scanf("%d",&n);
    p=n;
    for(int i=1;i<=n;i++){
        scanf("%d",&in[i]);
    }
    for(int i=1;i<=n;i++){
        scanf("%d",&post[i]);
    }
    for(int i=1;i<=n;i++){
        mp[in[i]]=i;
    }
    build(1,n);
    pre(1);
    printf("\n");

    return 0;
}

样例输入输出

输入：
9
4 2 5 1 6 3 8 7 9 //中序
4 5 2 6 8 9 7 3 1 //后序
输出：
124536789 //前序