自存！！！可看，勿喷QWQ

splay是平衡树，但不完全平衡

核心：每操作一个节点，均将该节点旋转到树根

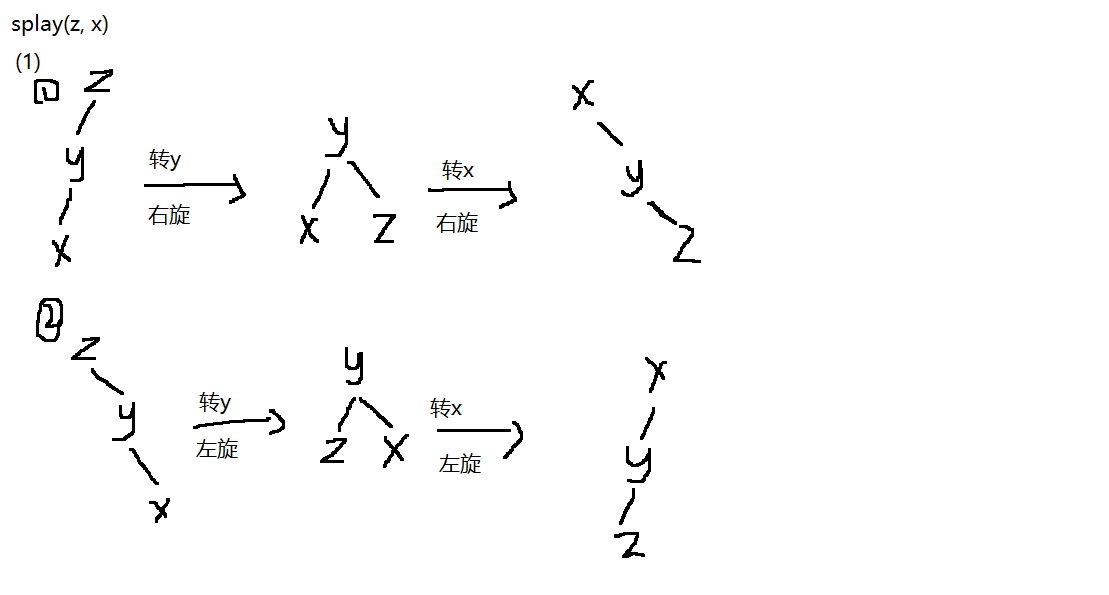
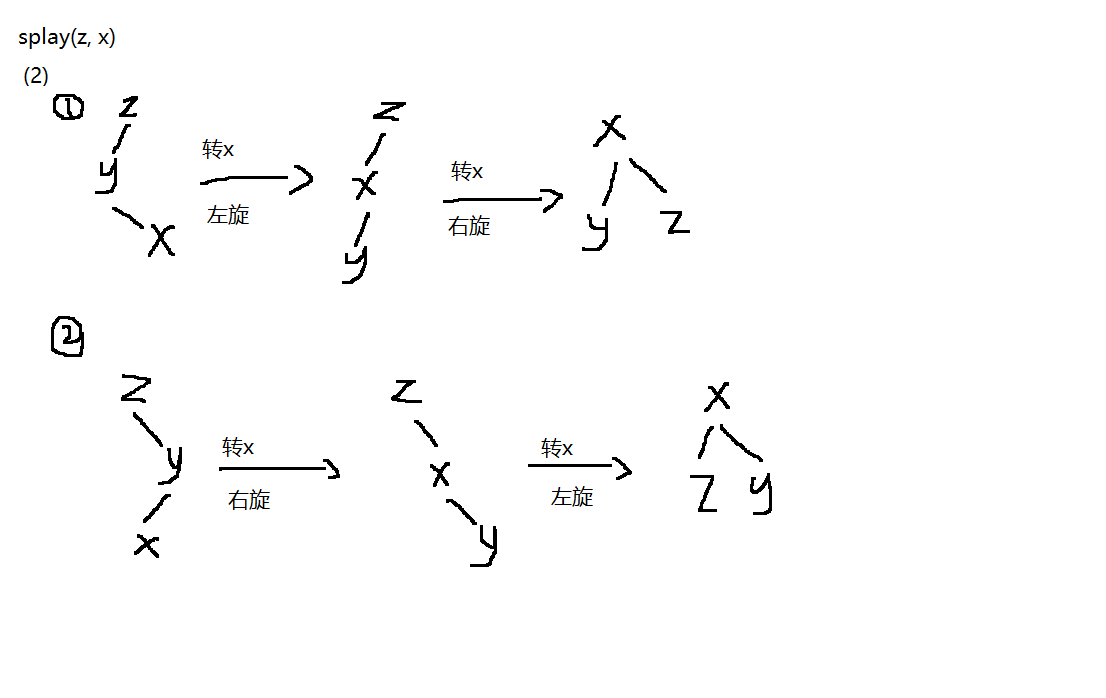
splay(x , k)：把点 x 旋转到点 k 下面

splay(x , 0)：将点x旋转到根节点

操作：

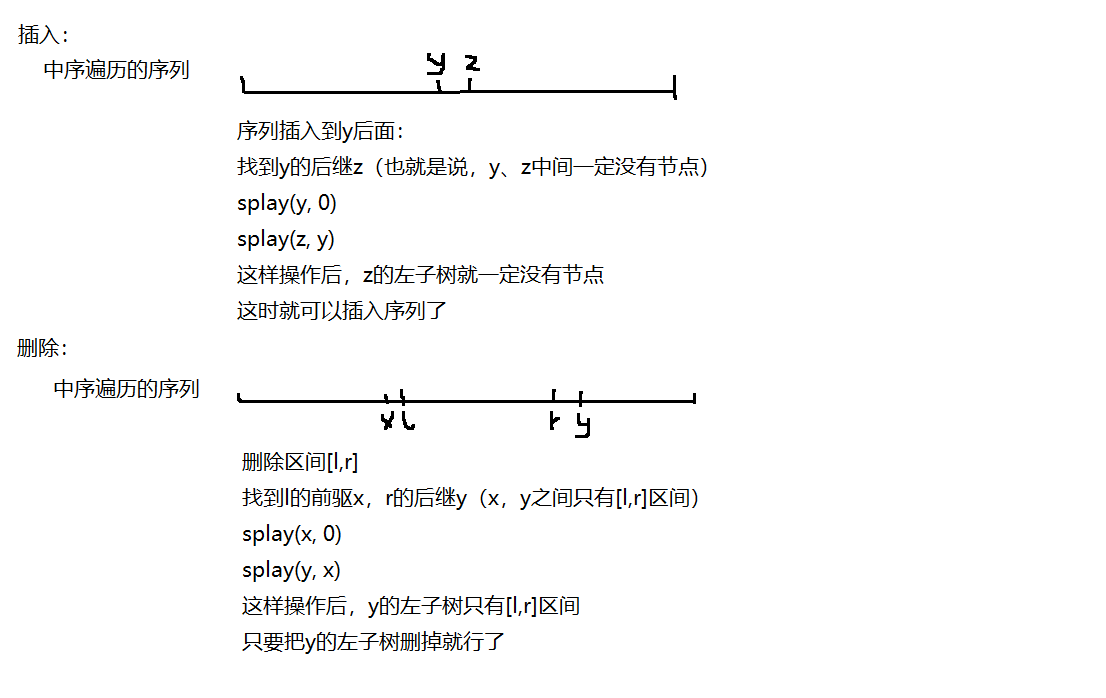
①插入 
  （1）直接插
  （2）将一个序列插到 y 的后面
          找到 y 的后继 z
         【1】将 y 转到根    splay( y , 0 )
         【2】将 z 转到 y 的下面   splay( z , y )
然后插入序列
②删除区间[l, r]
找到l的前驱x，r的后继y
【1】将x转到根 splay(x, 0)
【2】将y转到根 splay(y, x)
删除y的左子树

左旋右转合并写法

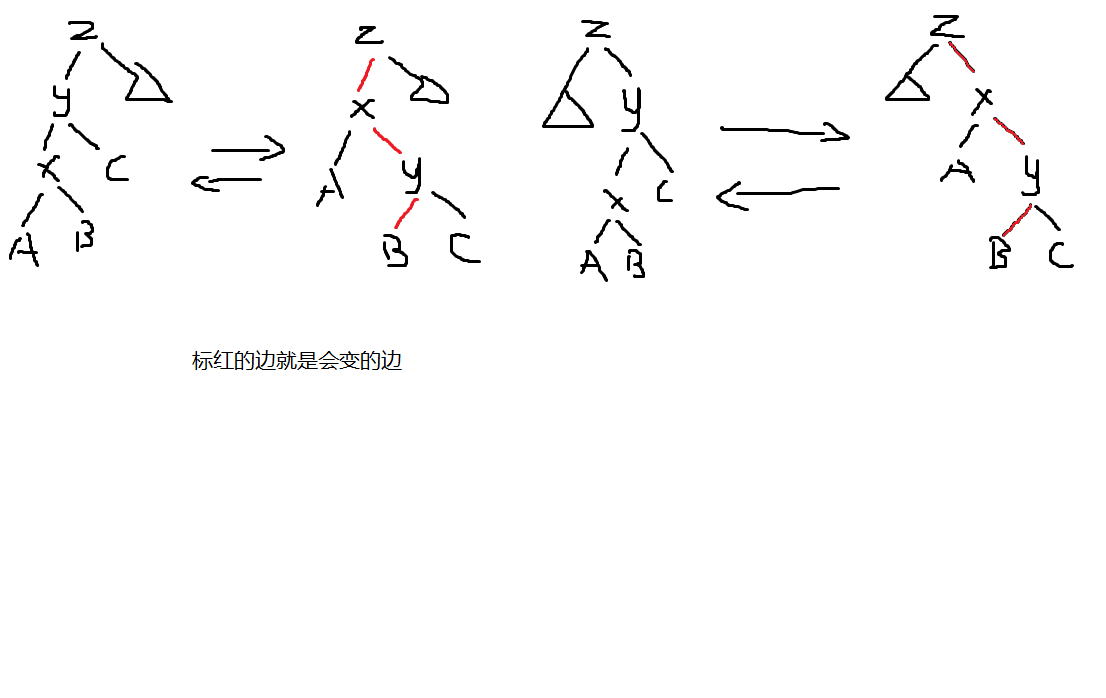
void rotate(int x)  // 旋转
{
    int y = tr[x].p, z = tr[y].p;
    int k = tr[y].s[1] == x;
    tr[z].s[tr[z].s[1] == y] = x, tr[x].p = z;
    tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y;
    tr[x].s[k ^ 1] = y, tr[y].p = x;
    pushup(y), pushup(x);
}

基本写法

struct Splay 
{
    int s[2], p, v;
    int size;

    void init(int _v, int _p)
    {
        v = _v, p = _p;
        size = 1;
    }
}tr[N];
//其中p指父亲节点，v是随机值（堆）
int root, idx;

void pushup(int x)
{
    // TODO: 利用子节点信息维护当前节点信息
}

void pushdown(int x)
{
    // TODO: 将懒标记下传
}

void rotate(int x)  // 旋转
{
    int y = tr[x].p, z = tr[y].p;
    int k = tr[y].s[1] == x;
    tr[z].s[tr[z].s[1] == y] = x, tr[x].p = z;
    tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y;
    tr[x].s[k ^ 1] = y, tr[y].p = x;
    pushup(y), pushup(x);
}

void splay(int x, int k)  // splay操作
{
    while (tr[x].p != k)
    {
        int y = tr[x].p, z = tr[y].p;
        if (z != k)
            if ((tr[y].s[1] == x) ^ (tr[z].s[1] == y)) rotate(x);
            else rotate(y);
        rotate(x);
    }
    if (!k) root = x;
}

void insert(int v)
{
    int u = root, p = 0;
    while (u) p = u, u = tr[u].s[v > tr[u].v];
    u = ++ idx;
    if (p) tr[p].s[v > tr[p].v] = u;
    tr[u].init(v, p);
    splay(u, 0);
}

int get_k(int k)
{
    int u = root;
    while (true)
    {
        pushdown(u);
        if (tr[tr[u].s[0]].size >= k) u = tr[u].s[0];
        else if (tr[tr[u].s[0]].size + 1 == k) return u;
        else k -= tr[tr[u].s[0]].size + 1, u = tr[u].s[1];
    }
    return -1;
}