一维前缀和

题目表述：求在区间 [l,r] 内所有的数的总和

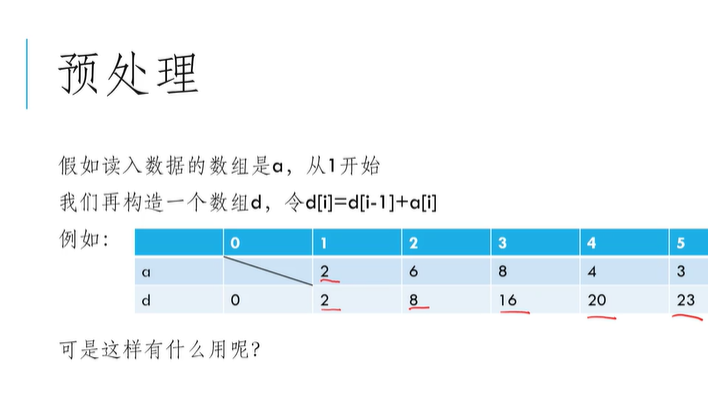
模板：

初始化： d[i] = a[1] + a[2] + ... a[i] = d[i-1]+a[i]
结论：   a[l] + ... + a[r] = d[r] - d[l - 1]

(补充)： P1115 最大子段和

/*
求最长子数组和 
*/ 

#include<bits/stdc++.h>
using namespace std;
const int N = 2e4+10;
int a[N];
int sum[N];
int main(){
    int maxx = 0;
    int n;cin >> n;
    for(int i = 0;i < n;i ++){
        cin >> a[i];
        sum[i] = sum[i-1] + a[i];
         maxx = max(maxx , sum[i]);//前缀和
    }
    for(int i = 0;i < n;i++){
        int l = 0;
        while(l <= i){
            if(sum[i] > maxx) maxx =sum[i];
            sum[i] -= a[l++];
        }
    }
    cout<< maxx <<'\n';
    return 0;
} 

想了一个写法，受到尺取法的启发
但是这个时间复杂度还是太高了，
因为$while(l<=i)$这一步的计算量是 $O(n)$
故引入一个新数组记录当前最大的子数组和

#include<bits/stdc++.h>
using namespace std;

//前缀和
//怎么表示一段区间
//b[i]表示到当前为止(i)连续且非空和最大值 

const int N=2e4+10;
int a[N];
int c[N];
int b[N];

int main()
{   int n,minn,mann;
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        c[i]=c[i-1]+a[i];//2 -2 1 0 2 -2 1
    }
    b[1]=a[1];minn=min(0,c[1]);//2 0 
    for(int i=2;i<=n;i++)
    {
        b[i]=c[i]-minn;//-2 -1 2 4 
        minn=min(minn,c[i]);//-2 
    }
    for(int i=1;i<=n;i++) mann=max(mann,b[i]);
    cout<<mann<<endl;
}

这道题可以拓展到$dp$
如果一个数加上上一个有效序列得到的结果比这个数大，那么该数也属于这个有效序列。 如果一个数加上上一个有效序列得到的结果比这个数小，那么这个数单独成为一个新的有效序列
$ans[i]=max(ans[i-1]+n[i],n[i])$;//DP

#include<bits/stdc++.h>
using namespace std;

const int N =2e4+10;
int a[N];
int dp[N];
int main(){
    int n;cin >> n;
    int ans=0;
    for(int i =1;i<=n;i++){
        cin >>a[i];
        if(i<2) dp[i] = a[i];
        else dp[i] = max(dp[i-1]+a[i],a[i]);
        ans = max(ans,dp[i]);
    } 
    cout<<ans<<endl;

} 

二维前缀和

初始化： s[i][j]=a[i][j]+s[i-1][j]+s[i][j-1]-s[i-1][j-1];

S[i][j] = 第i行j列格子左上部分所有元素的和
以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为：
结论： a[x2][y2] - S[x1 - 1][ y2] - S[x2][y1 - 1] + S[x1 - 1][ y1 - 1]

一维差分

题目表述： 在区间[l,r] ，对它进行 m 次区间修改(在区间所有书加上 或 减去一个数) ，输出修改后的序列

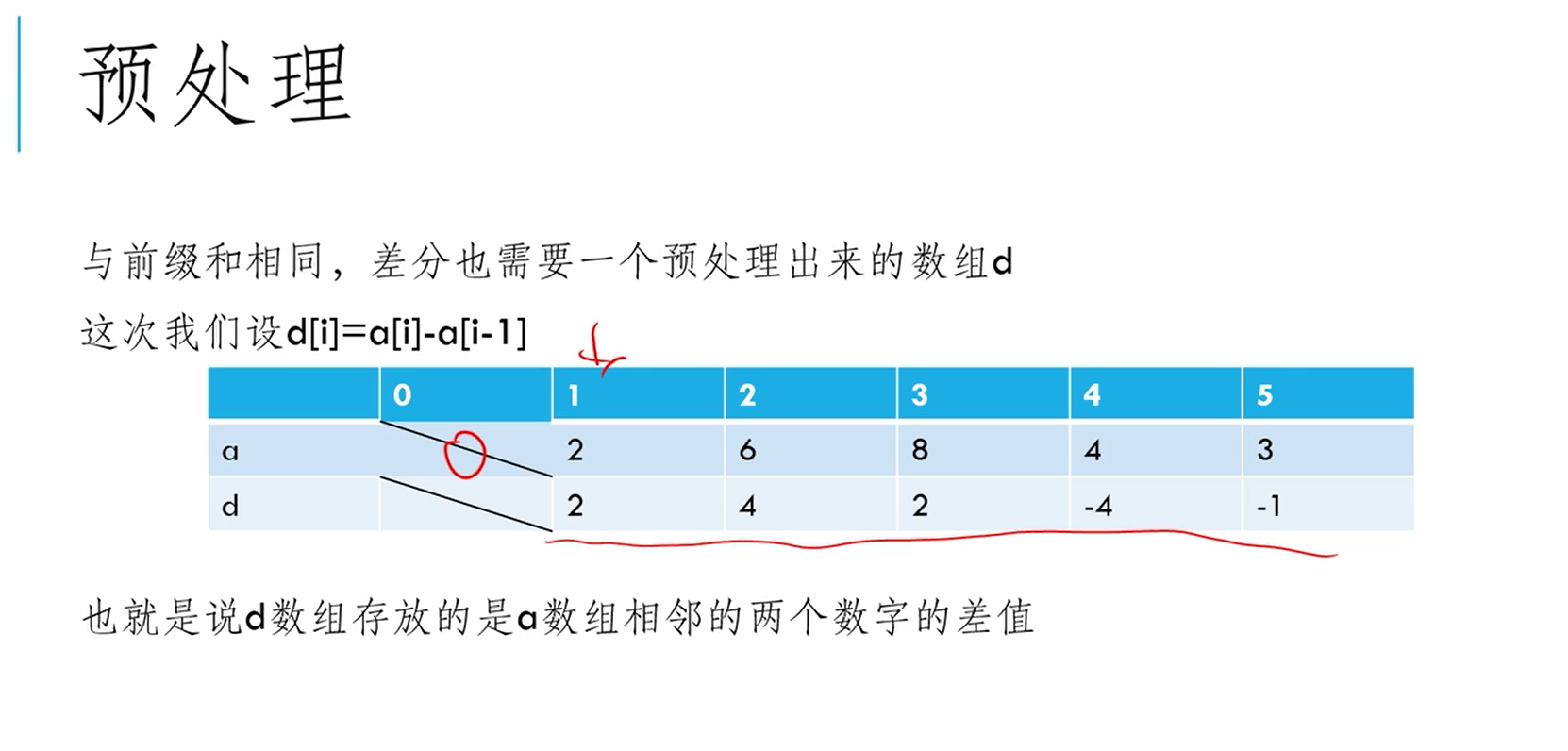
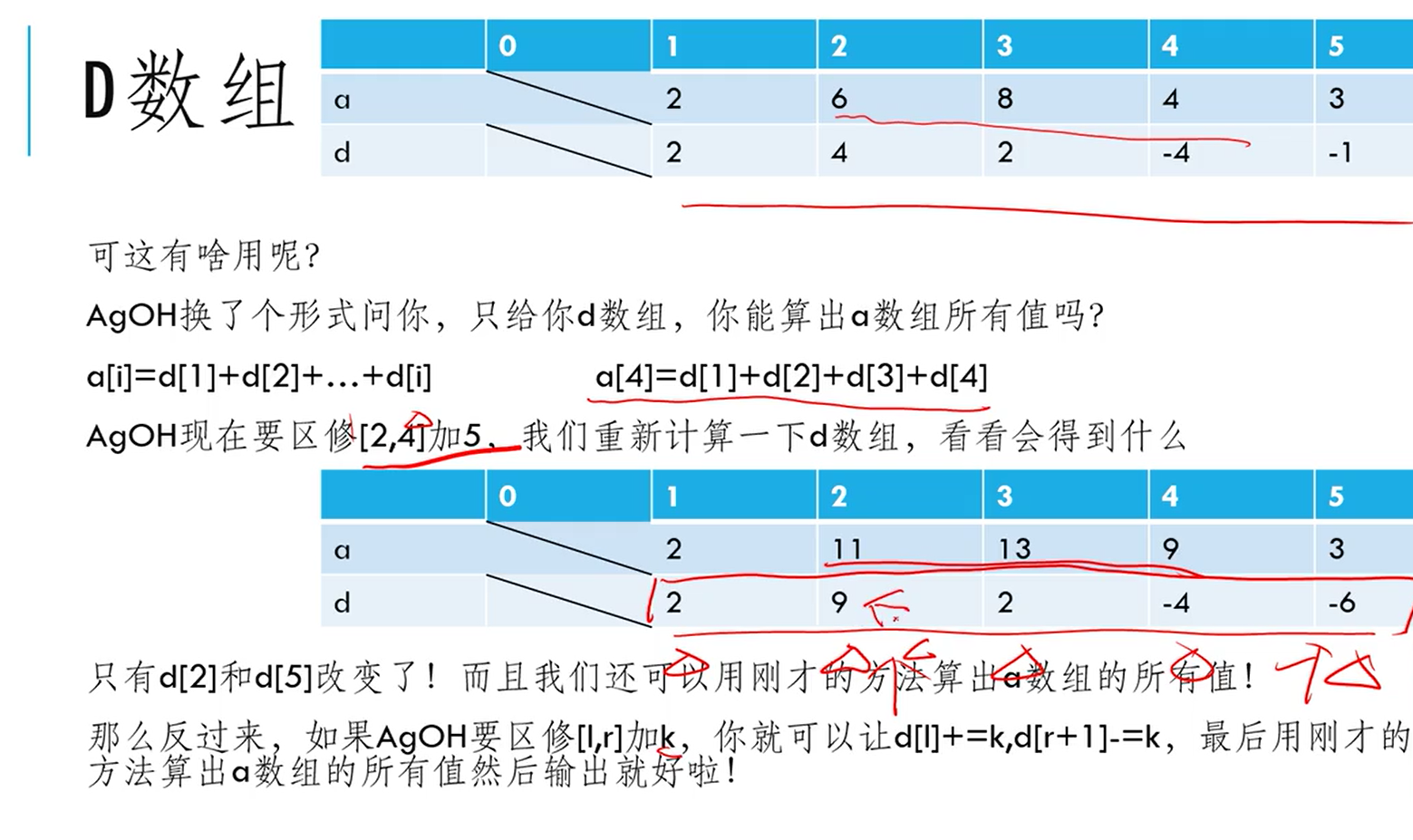
模板

a[i]=d[1]+d[2]+...+d[i];

结论：在区间 [l,r] 加 k, d[l]+=k,d[r+1]-=k;
最终值表示： a[i]=a[i-1] + d[i]  推算出区间各个数值

模板题： 一维差分
运用了 前缀和 和 差分

#include<bits/stdc++.h>
using namespace std;
int a[110];
int d[110];
int main(){
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>a[i];//原数组
    for(int i=1;i<=n;i++) d[i]=a[i]-a[i-1]; //差分数组 

    while(m--){
        int x,y,z;
        cin>>x>>y>>z;
        d[x]+=z;//结论 
        d[y+1]-=z;

    }
    for(int i=1;i<=n;i++) a[i]=a[i-1]+d[i];//计算原数组 = 差分数组的前缀和  
    for(int i=1;i<=n;i++) cout<<a[i]<<" ";


    return 0;
}

二维差分

给以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵中的所有元素加上c：
S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c