数论，我以前都是记公式记公式，应该现尽可能的理解

比如，我只知道埃氏筛，现在线性筛的原理是被最小质因数标记掉，所以有if(i % prime[j] == 0) break;

比如 4 % 2 == 0， 所以不用标记 4 * 3( = 12) 显然 12 会被6 * 2 标记掉 （12的最小质因数是2）

约数个数

原来这么好理解，呜呜，我是笨蛋

重点是分解

就可以顺势理解 约数个数 每个pi都有（ai + 1）种可能

约数和 每个约束为 p0^b ~ pi ^bi 任意组合

睡觉觉，感冒感冒快走开

约数个数

呃，用unordered_map，其实就是hash比map快，为什么要用到呢，其实不用，but约数和要用到，这样两个代码相似，改改快些

tip:分解质因数 复杂度为 but有可能 分解完n不是1，那么这也是质因数

欧拉函数

到与互质的个数

原来这么好理解，是容斥啊

是 res = res / i * (i - 1); 不是 res = res * （1 - 1 / i) (因为i是整数)，不是res = res * （i - 1 ) / i 怕爆int

筛法求欧拉函数

根据线性筛的基础上，（为什么能够筛掉所有的数，在什么时候求欧拉函数？ 再标记is_pri[i] = 1时，这样保证所有数都被算到，且只被算到一次）

分三种情况：

1）这数是质数，那一定与其他所有数（除去自己）互质 phi [i] = i - 1;

//2） 3）部分是往后筛的时候确定欧拉的，往后筛的数是 prime[j] * i

2）这数不是质数，且这数是prime[j] 的倍数，那么相当于欧拉公式后面（1 - 1 / p_k)一串不变，变的是n,n由 i 变为 i * prime[j] ,所以 phi[i * prime[j]] = phi[i] * prime[j];

3）这数不是质数，且这数不是prime[j] 的倍数, 而prime[j] 一定是 i * prime[j] 的因数，所以相当于 多了一个不一样的 质因数，相当于在phi[i] 上 多乘了 prime[j] 和 (1 - 1 / prime[j]) , 所以 phi[i * prime[j]] = phi[i] * (prime[j] - 1);

欧拉定理

n,a为正整数，且n,a互质，则:

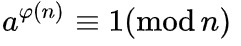
快速幂

没啥好说的，小tip：ans = ans * x % mod; // 不可以写成 ans *= x % mod;

费马小定理

没啥好说的，小tip：要求两个互质 ，逆元=a ^ (p - 2 ) % p， p是质数

裴蜀定理

若a,b是整数,且gcd(a,b)=d，那么对于任意的整数x,y, ax+by都一定是d的倍数，一定存在非零整数x,y，使ax+by=e(e = a和b的最小公倍数) 成立。

拓展欧几里得

推导：

$a \times x + b \times y \equiv d(d = gcd(a, b)) 得 $

$b \times y + (a\%b) \times x \equiv d,而 a \% b = a - b * \lfloor\frac{a}{b}\rfloor$

所以化简为$a \times x + b \times (y - b \times \lfloor \frac{a}{b} \rfloor \times x)\equiv d$

代码要熟练

高斯消元

其实我步骤一直都会，只是一直没有用心去背

首先是要有这个意识叭，然后付诸行动！！！

tip：好的变量名可以减少记忆量！

异或运算，是不进位的加法

重点是运算过程！！

组合数

模板一

预处理出所有的 $C^b_a = C_{a - 1}^{b - 1} + C_{a - 1}^{b}$

模板二

运用逆元的思想,这样a，b的范围可以达到1e6

$C^b_a = \frac{a!}{(a - b)! \times b!}$

模板三

lucas定理

a,b范围可以达到1e18 , p 是 1e5

重点是公式

$C_a^b \equiv C_{a\ mod\ p}^{b\ mod \ p} \times C_{a/p} ^ {b/p} (mod\ p)$

2.13总结

O^2, O^3优化

 #pragma GCC optimize(2)
 #pragma GCC optimize(3,"Ofast","inline")

模板四

对于不mod的情况，a,b可以为5e3

$C^b_a = \frac{a!}{(a - b)! \times b!}$

a的阶乘，可以分解为$p_1^{c_1} \times p_2^{c_2} \times p_3^{c_3} \times p_4^{c_4}…$

$c_1 = \lfloor\frac{a}{p_1}\rfloor + \lfloor\frac{a}{{p_1}^2}\rfloor + \lfloor\frac{a}{{p_1}^3}\rfloor…$

要用到高精度乘法

卡特兰数（待细细整理

$C_{2n}^{n} - C_{2n}^{n-1} = \frac{C_{2n}^{n}}{n + 1}$

容斥定理

用位运算,状态压缩

NIM博弈论

寻找到必败态，标记为0

SG函数

必败态标记为0，递归

//距离递归算SG

 int s[MAX];
 int f[10010];
 
 int SG(int x) {
     if(f[x] != -1) return f[x];
     unordered_set<int>ss; //对于每一个分叉，根不算，所有的节点找mex
     for(int i = 0; i < n; i++) {
         if(x >= s[i]) {
             ss.insert(SG(x - s[i]));
         }
     }
     for(int i = 0; ; i++) {
         if(!ss.count(i)) return f[x] = i;
     }
 }

拆分-Nim游戏有点意思

去重,去掉连续的重复的

 n = unique(a + 1, a + 1 + n) - a - 1;