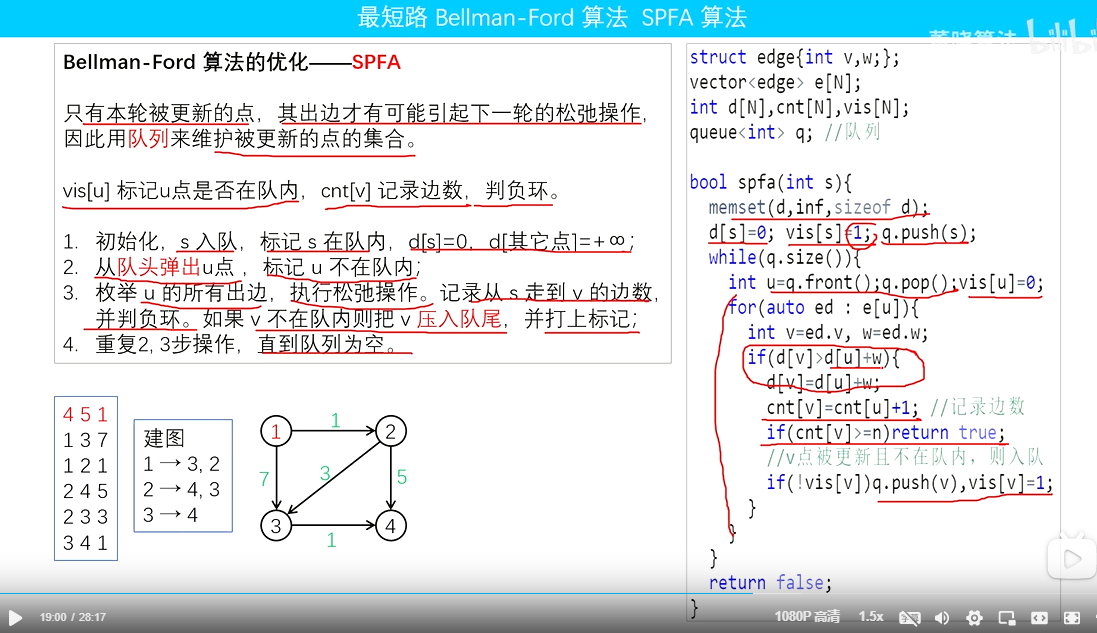
/
最短路spfa的流程
1.单源最短路
2.是贝尔曼算法的队列优化
3.可以用来判负环
1.vis[u]判断u点是否在队内，cnt[v]用来判断到v点的时候是否真的有负环，判负环
2.初始化，源点S入队，标记S在对内，d[s]=0,d[其他点]=inf
3.枚举u的所有出边，执行松弛操作。记录从S到v的边数，并判负环 。
如果v不在对内则把v压入队尾，并打上标记
4.
：这里对cnt[v]进行详细解释一下：
cnt[v]=cnt[u]+1(当u点对v点进行松弛操作：if d[v]>d[u]+w)
松弛的边数+1
当cnt[v]>=n时，表示存在负环 ：因为最短路n个点的话，最多松弛n-1条边，注意是一条最短路哦
：还有一个需要注意的点就是：这里使用的是队列而不是优先队列哦
这里的点是可以多次入队的，当入队时，vis[u]=1,出对时，vis[u] =0
入队时机：当v被更新，v入队
出队时机：当u被用来更新其他点时，pop后，vis[u]=0;
:这里似乎好像没有用到贪心的思想
/

#include<bits/stdc++.h>

using namespace std;

struct edge{
    int v,w;
};

vector<edge> e[N];

int d[N],cnt[N],vis[N];

queue<int> q;

bool spfa(int s){
    memset(d,inf,sizeof(d));
    d[s] =0;vis[i]=1;q.push(s);
    while(q.size()){
        auto u = q.front();q.pop();vis[u]=0;
        for(auto ed:e[u]){
            int v =ed.v, w=ed.w;

            if(d[v] > d[u] + w){
                d[v] = d[u] +w;
                cnt[v] = cnt[u] + 1;
                if(cnt[v] >= n) return true;

                if(!vis[v]) q.push(v), vis[v] =1; 
            }
        }
    } 

    return false;
}

int main(){

}