二进制中 1 的个数

补充：

一个数$&$ 1的结果就是取二进制的最末位，还可以判断奇偶 $x & 1==0 $为偶，$x & 1==1$为奇。
运算符 $>> $, 二进制去掉最后一位

步骤：

1） 先将二进制数向右移动 k位(此时 k位移动到了第一位), 操作: x >> k
2） 获取最后一位的值, 操作: 移动后的值 & 1 是否为 1

注意点： 强制转换成无符号操作(因为考虑到负数)
在C++中如果我们右移一个负整数，系统会自动在最高位补1，这样会导致 un 永远不为0，就死循环了。
解决办法: 把 un 强制转化成无符号整型，这样 n 的二进制表示不会发生改变，但在右移时系统会自动在最高位补0。

位运算

模板

class Solution {
public:
    int NumberOf1(int n) {
        int res = 0;
        unsigned int un = n; //要用无符号的
        while (un) res += un & 1, un >>= 1;
        return res;
    }
};

法二：（时间复杂度更低）
将n - 1后再和n相与，得到的值相当于将n从右边数的第一个1变成0。
n的二进制表示中有多少个1，就能变多少次

public int NumberOf1(int n)
{
    int count = 0;
    while (n != 0)
    {
        count++;
        n = (n - 1) & n;
    }
    return count;
}

例题补充： 数列
注意：可以把 N 转化成 二进制，二进制对应是1 就加上相应幂次方

$ N=1 ----> 1 ----> 3(0)$
$ N=2 ----> 10 ----> 3(1)$
$N=3 ----> 11 ----> 3(0)+3(1)$
$ N=4 ----> 100 ----> 3(2)$
$N=5 ----> 101 ----> 3(0)+3(2)$

完整代码：

#include<bits/stdc++.h>
using namespace std;

int k, N;

int main()
{
    cin >> k >> N;
    int res = 0, t = 1;
    while (N)
    {
        if (N & 1) res += t;
        t *= k;
        N >>= 1;
    }
    cout << res << endl;
    return 0;
}

返回x的最后一位1：lowbit(x) = x & -x= x & (∼x+1)

就是每一次把 x 的最后一位 1 减掉，即 x−lowbit(x)，只需要算下减多少次，减多少次就有多少个 1

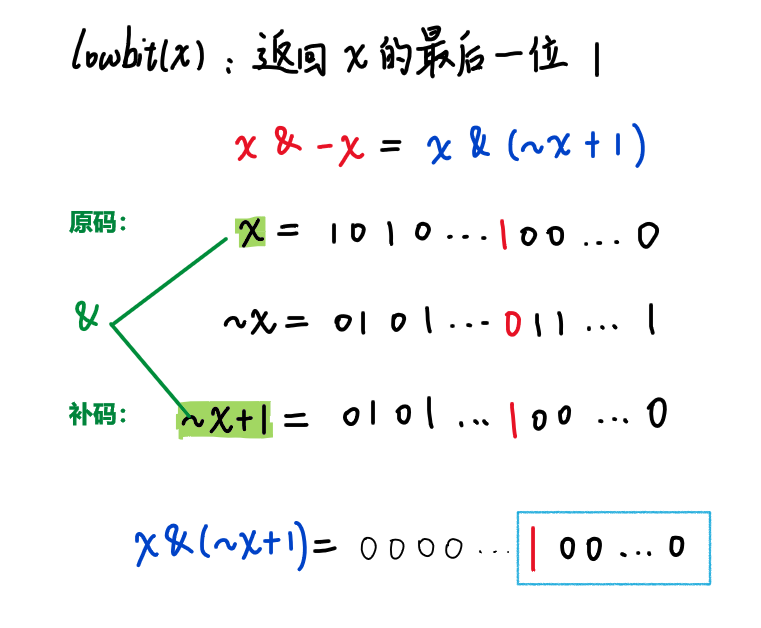
$lowbit(x) 操作返回 x 的最后一位 1$
$x=1010，那么 lowbit(x) 返回 10，即 lowbit(x)=10$
$ x=101000，那么 lowbit(x)返回 1000，即 lowbit(x)=1000$

模板如下：

int lowbit(int x)
{
    return x&(-x);
}

参考资料