二分图的判定

定义：就是可以将一张无向图中的点分成两个团，团内的点与点之间是没有连线的

定理：二分图不存在奇环

因为每一条边都是从一个集合走到另一个集合，只有走偶数次才能回到同一个集合

染色法

即尝试用两种颜色标记图中的节点，当一个点被标记后，
所有与他相邻(也可以说是相连吧)的节点标记为相反颜色，就是一个0一个1别，
若标记过程中产生冲突，则说明途中存在**奇环**。可以使用DFS或BFS来实现

#include<bits/stdc++.h>

using namespace std;

const int N=1e5+10,M=2*N;

int n,m;
struct edge{
    int v,ne;
}e[M];

int h[N],idx;
int color[N];

void add(int a,int b){
    e[++idx]={b,h[a]};
    h[a]=idx;
}

bool dfs(int u,int c){
    color[u] = c;
    for(int i=h[u];i;i=e[i].ne){
        int v = e[i].v;//这条边的终点 
        if(!color[v]){
            if(dfs(v,3-c)) return 1;
        }
        else if(color[v] == c) return 1;//有奇环 
    }
    return 0; 
}

int main(){
    cin>> n>>m;
    for(int i=1;i<=n;i++){
        int a,b;
        cin>>a>>b;
        add(a,b);
        add(b,a);
    }
    bool flag=0;

    for(int i=1;i<=n;i++){
        if(!color[i]){
            if(dfs(i,1)){
                flag=1;
                break;
            }
        }
    }
    if(flag==1)puts("NO");//不是二分图
    else puts("Yes");//是二分图 
    return 0; 
}

图片

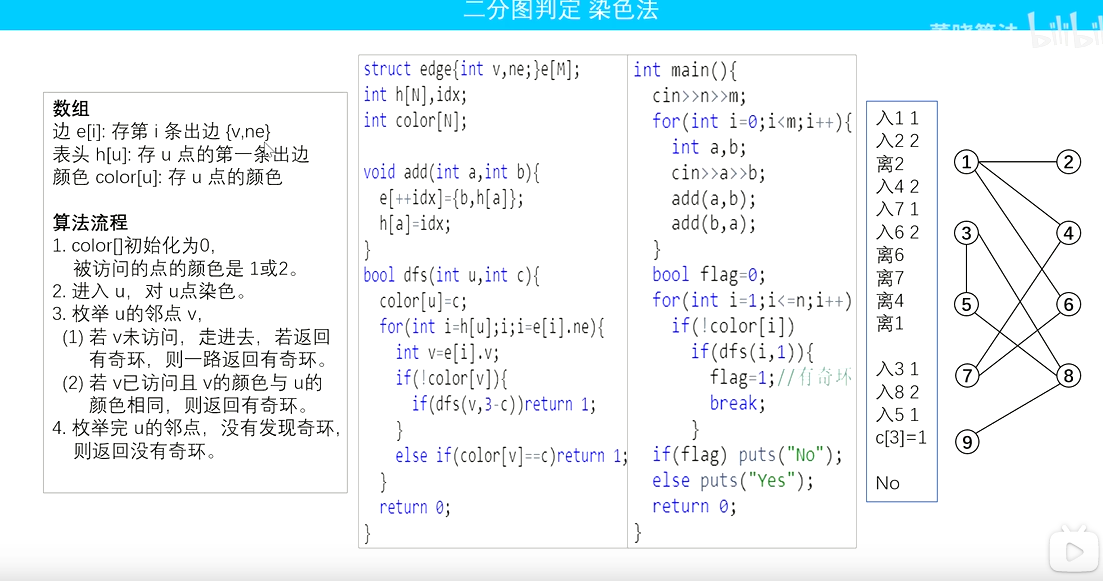
边的存储解释

void add(int a,int b){
e[++idx]={b,h[a]};
h[a]=idx;
}