引论

对网络流算法的认识

网络流算法是一种高效实用的算法，相对于其它图论算法来说，模型更加复杂，编程复杂度也更高，但是它综合了图论中的其它一些算法（如最短路径），因而适用范围也更广，经常能够很好地解决一些搜索与动态规划无法解决的，看似 $\rm NP$ 的问题。

具体问题的应用

网络流在具体问题中的应用，最具挑战性的部分是模型的构造。这没有现成的模式可以套用，需要对各种网络流的性质了如指掌（比如点有容量、容量有上下限、多重边等等），并且归纳总结一些经验，发挥我们的创造性。

网络流有许多分支的问题，这里只为大家介绍最大流问题。涉及到 $\rm FF,EK,Dinic$ 三个算法。
注意：网络流部分的课程当中也有“增广路径”的概念，但这与匈牙利算法当中的增广路径含义不同。

• 二分图：通过拓展增广路径来获得更多的匹配
• 最大流：通过寻找增广路径来获取更大的流量

什么是网络流？

我们从一个简单的例子开始说起。
你所在的村庄新开通了地下流水管道，自来水厂源源不断的提供水，村民们用水直接或间接用水，而村庄用完的废水统一回收于另一点(设排来的水全部回收)。当然每个管道有一定的容量。求废水站最多可以汇聚多少水？
当然这是一个有向图。所有的水都从一个点流出（水厂），最后全部汇聚到一个点（废水站）。

网络流图

一个网络流图是一个没有自环的有向连通图，满足：
只有一个入度为 $0$ 的点 $S$，称为 源；
只有一个出度为 $0$ 的点 $T$，称为 汇；
每条边 $e=(i, j)$ 有一个非负实数权值 $c_e$，称为该边的容量。

容许流

在网络流图中，对于每条边 $e=(i, j)$ 给定实数 $f_e$ 为该边的流量，如果满足

• 每条边的流量不大于容量（$f_e \leqslant c_e$）
• 每个点的入流量等于出流量（对于 $x \neq S, T$，$\sum\limits_{e=(x, i)} f_e = \sum\limits_{e=(i, x)} f_e$）
• 源点流出等于汇点流入 $W = \sum\limits_{e=(S, i)} f_e = \sum\limits_{e=(i, T)} f_e$

则这一组流量 $f$ 称为该网络的一个容许流，$W$ 称为它的流量。
最大流：求一个容许流使得它的 $W$ 最大。

最大流算法

基本思路：
从流量为 $0$ 的容许流开始，不断尝试寻找增流路径（增广路），增加容许流的流量，直到无法增加为止。
称为增广过程。

Ford-Fulkerson 标号算法

记录 $v_e = c_e - f_e$，为一条边的剩余容量。
定义残量网络：对于每条边 $e=(u, v)$，其边权为 $v_e$，并对其增加一条反向边 $e’=(v, u)$，边权为 $f_e$。
每次在残量网络中，任意找一条从 $S$ 到 $T$ 的路径，边权均不为 $0$，则这条路径成为一条增广路，这条路径上边权的最小值 $w$ 为容许流流量的增量。
将这条路径上每一条边 $e$ 的边权减去 $w$，并将其反向边 $e’$ 的边权加上 $w$。
若 $e$ 为原图中的一条边，则相当于将该边的 $f$ 增加了 $w$；否则相当于将 $e’$ 的 $f$ 减少了 $w$（退流）。

正确性：
残量网络中每条边的边权不会变为负数，即保证了 $0 \leqslant f_e \leqslant c_e$；
每次增广时，一个点的入流量和出流量总是同时变化 $w$，总满足对于每个点的流量平衡；
每次增广时，$S$ 的出流量和 $T$ 的入流量会同时增加 $w$。
若存在最大流，则在最大流中每个点仍满足流量平衡，若要增加流量，则残量网络中必然存在满足要求的路径。
同时说明了只要最大流流量 $W$ 有限，总在有限的时间内求出。

代码实现

struct edge {
    int to, cap, rev;
};

vector<edge> g[MAX_V];
bool used[MAX_V];

// 向图中增加一条从 s 到 t 容量为 cap 的路径
void add_edge(int u, int v, int cap) {
    g[u].emplace_back(v, cap, g[v].size());
    g[v].emplace_back(u, 0, g[u].size()-1);
} 

// 通过 dfs 寻找增广路
int dfs(int v, int t, int f) {
    if (v == t) return f;
    used[v] = true;
    for (auto&& e : g[v]) {
        int d = dfs(e.to, t, min(f, e.cap));
        if (d > 0) {
            e.cap -= d;
            g[e.to][e.rev].cap += d;
            return d;
        }
    }
    return 0;
} 

// 求解从 s 到 t 的最大流
int max_flow(int s, int t) {
    int flow = 0;
    while (1) {
        memset(used, 0, sizeof used);
        int f = dfs(s, t, INF);
        if (f == 0) return flow;
        flow += f;
    }
}

Edmonds-Karp 算法

${\rm FF}$ 算法的效率问题：其复杂度与边权相关。
注意到在图中 $C$ 可能很大很大
比如说下面这张图

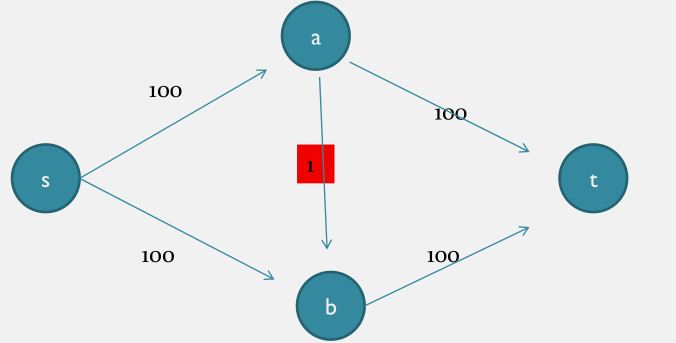
如果运气不好 这种图会让你的程序执行 $200$ 次dfs
虽然实际上最少只要 $2$ 次我们就能得到最大流

${\color{Blue} {Edmonds-Karp}}$ 算法：每次沿着一条最短（边数最少）的增广路进行增广。
在残量网络中寻找路径时使用 BFS 即可。
可以证明，${\rm EK}$ 算法的复杂度与边的容量无关，且增广路的条数不超过 $\frac{m(n+2)}{2}$。因此它的复杂度上界为 $O(m^2n)$（一般远达不到）。

Dinic 算法

考虑继续优化上述算法
在上述算法中，每一次我们只求出了一条增广路。
实际上，我们可以一次求出多条互不干扰的增广路进行增广。

每一次对残量网络进行分层：忽略边权为 $0$ 的边，求出 $S$ 到每个点 $i$ 的最短距离 $dist[i]$。
考虑所有满足不为 $0$ 且 $dist[i] + 1 = dist[j]$ 的边 $e=(i, j)$，这些边组成了一个 DAG，DAG 上任意一条从 $S$ 到 $T$ 的路径均为最短路。
在该 DAG上进行 ${\rm DFS}$ 即可一次求出多条增广路。

当前弧优化

在 ${\rm DFS}$ 的过程中，对于一条边 $e = (i, j)$，如果已经不存在一条 $j$ 到 $T$ 的可用路径，则这条用已经不能再用于增广了。
对于每个点，记录它可能用于增广的第一条边。在 ${\rm DFS}$ 的时候维护这个值，可以减少许多无用的搜索过程。

${\color{Green} {Dinic}} $ 算法的复杂度：

每次 ${\rm DFS}$ 结束后最短路的长度一定增加，故分层与 ${\rm DFS}$ 的次数为 $O(n)$
分层复杂度较低，瓶颈为 ${\rm DFS}$ 的复杂度：
成功增广的部分，最多增广 $m$ 次，每次最多 $n$ 条边，复杂度 $O(nm)$；
寻找增广路失败时后退的部分，由于当前弧优化，每次后退都会删除一条边，故复杂度 $O(m)$。
即总复杂度 $O(n^2m)$。

最大流最小割定理

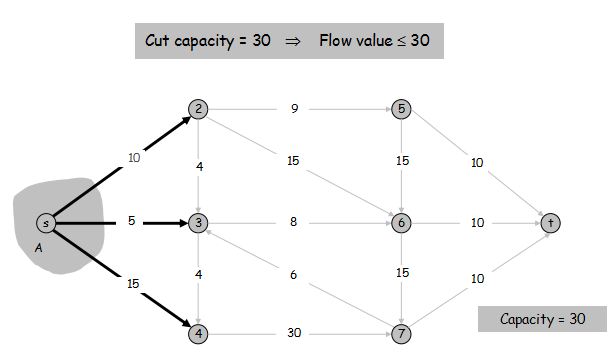
定义 s-t 割 是节点集 $V$ 的一个划分 $(A, B)$，使得 $s \in A$ 且 $t \in B$。
定义 (A, B) 割 的容量为 $cap(A, B) = \sum\limits_{e \text{：从}A\text{中引出的边}} c(e)$

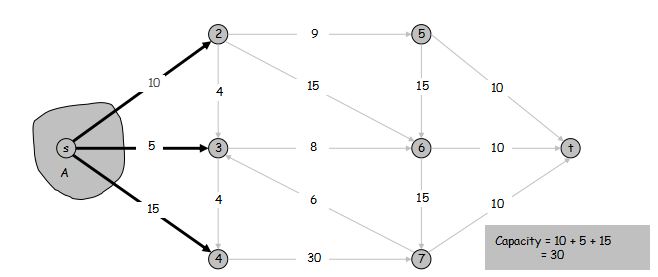
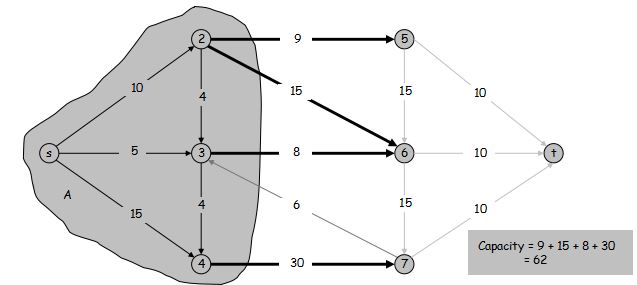
最小割问题： 找到一个 s-t 割 满足它的容量最小

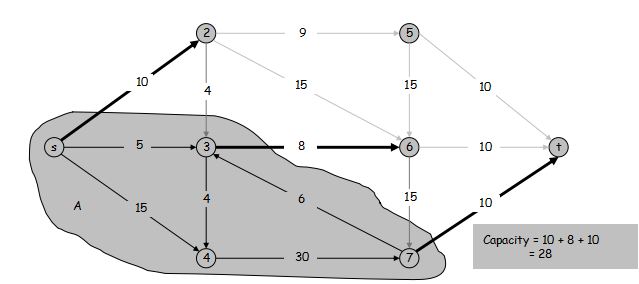
流值引理： 令 $f$ 为任意流，$(A, B)$ 为任意 s-t 割。从 $A$ 流出的量减去从 $A$ 流入的量等于流 $f$ 的流值，即 $\sum\limits_{\text{流出} A \text{的边} e} f(e) - \sum\limits_{\text{流入} A \text{的边} e} f(e) = v(f)$。

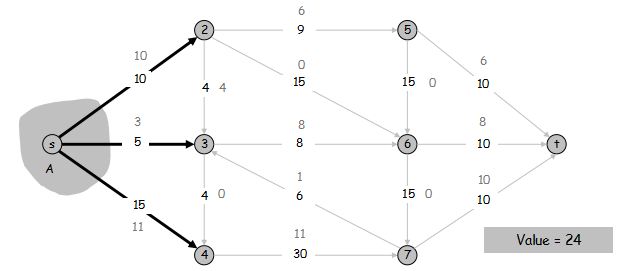
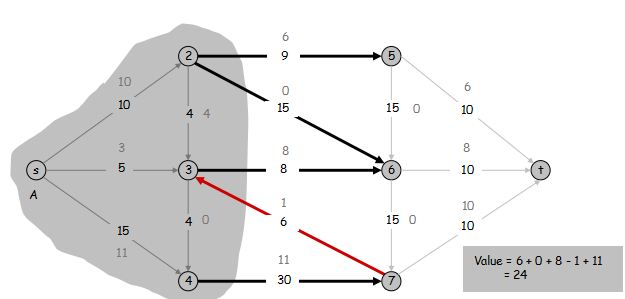
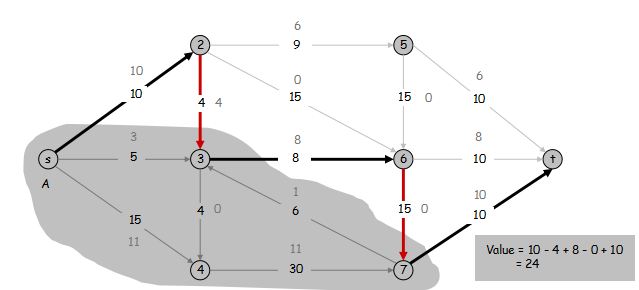
证明：

$v(f) = \sum\limits_{\text{流出} \ s \ \text{的边} e} f(e)$
根据流量守恒要求，$A$ 中所有点除了 $s$ 外，流入的量等于流出的量，因此 $$v(f) = \sum\limits_{v \in A} (\sum\limits_{\text{流出} \ v \ \text{的边} e} f(e) - \sum\limits_{\text{流入} \ v \ \text{的边} e} f(e))$$

若一条边的两端点都在 $A$ 中，一定对应着一正一负的两项可以消掉，所以 $$v(f) = \sum\limits_{\text{流出} \ A \ \text{的边} e} f(e) - \sum\limits_{\text{流入} \ A \ \text{的边} e} f(e)$$

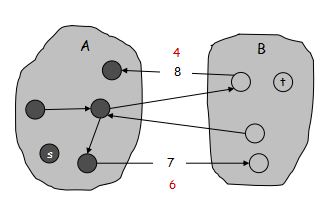
弱对偶性： 令 $f$ 为任意的流，$(A, B)$ 为任意的 s-t 割，那么 $f$ 的流值不超过割的容量。

证明：

$ \begin{aligned} v(f) &= \sum\limits_{\text{流出} \ A \ \text{的边} e} f(e) - \sum\limits_{\text{流入} \ A \ \text{的边} e} f(e) \\\ &\leqslant \sum\limits_{\text{流出} \ A \ \text{的边} e} f(e) \\\ &\leqslant \sum\limits_{\text{流出} \ A \ \text{的边} e} c(e) \\\ &= cap(A, B) \end{aligned} $

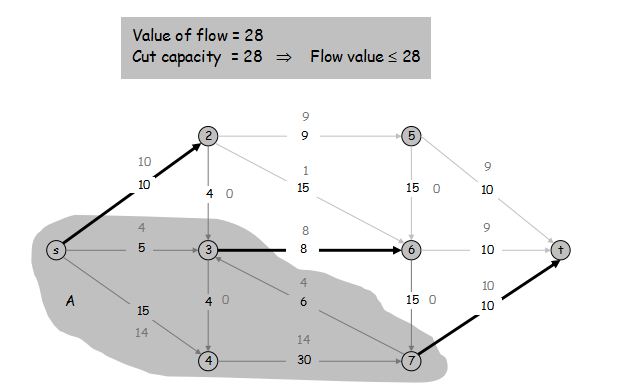
最优性条件： 令 $f$ 为任意的流，$(A, B)$ 为任意的割。如果 $v(f) = cap(A, B)$，那么 $f$ 是最大流且 $(A, B)$ 是最小割。

增广路定理： $f$ 为最大流当且仅当没有增广路。

最大流最小割定理： 最大流的流值等于最小割的容量。

我们可以通过证明以下三个命题的等价性来证明以上两个定理。

$(i)$ 存在一个割 $(A, B)$ 使得 $v(f) = cap(A, B)$
$(ii)$ $f$ 是一个最大流
$(iii)$ 对于 $f$，网络中不存在增广路

$(i) \to (ii)$ 这是弱对偶引理的推论
$(ii) \to (iii)$ 我们证明它的逆否命题。
令 $f$ 是一个流。如果存在一条增广路，那么我们可以沿着这条增广路进行增广来提高流值，则 $f$ 不是最大流。
$(iii) \to (i)$ 令 $f$ 为一个流，对应的残量网络中不存在增广路，$A$ 为残量网络中由 $s$ 可达的节点集合
由 $A$ 的定义，$s \in A$。由 $f$ 的定义，$t \notin A$。

$ \begin{aligned} v(f) &= \sum\limits_{\text{流出} \ A \ \text{的边} e} f(e) - \sum\limits_{\text{流入} \ A \ \text{的边} e} f(e) \\\ &= \sum\limits_{\text{流出} \ A \ \text{的边} e} c(e) \\\ &= cap(A, B) \end{aligned} $

最小费用最大流（费用流）

根据增广路定理，我们只需要不断地走增广路就能找到最大流
所以我们每次找一条单位费用最小的增广路，然后进行增广，直到找不到

其中单位费用最小其实就是最短路问题