线段树
线段树的打法大致有两种
以区间信息加法统计为例
第一种
const int N
int a[N];
struct TREE
{
int l,r,dat,add;
}t[N*4];
void build(int rt,int l,int r)
{
//建树
t[rt].l=l,t[rt].r=r;
if(l==r)
{
t[rt].dat=a[l];
return ;
}
int mid=(l+r)>>1;
build(rt<<1,l,mid);
build(rt<<1|1,mid+1,r);
t[rt].dat=t[rt<<1].dat+t[rt<<1|1].dat;
}
void spread(int rt)
{
//懒标记传递
if(t[rt].add)
{
t[rt<<1].dat+=t[rt].add*(t[rt<<1].r-t[rt<<1].l+1),t[rt<<1].add+=t[rt].add;
t[rt<<1|1].dat+=t[rt].add*(t[rt<<1|1].r-t[rt<<1|1].r+1),t[rt<<1|1].add+=t[rt].add;
t[rt].add=0;
}
}
void change(int rt,int l,int r,int k)
{
//区间修改
if(l<=t[rt].l&&r>=t[rt].r)
{
t[rt].dat+=k*(t[rt].r-t[rt].l+1);
t[rt].add+=k;
return ;
}
spread(rt);
int mid=(t[rt].l+t[rt].r)>>1;
if(l<=mid) change(rt<<1,l,r,k);
if(r>=mid+1) change(rt<<1|1,l,r,k);
t[rt].dat=t[rt<<1].dat+t[rt<<1|1].dat;
}
int query(int rt,int l,int r)
{
//区间查询
if(l<=t[rt].l&&r>=t[rt].r)
{
return t[rt].dat;
}
spread(rt);
int mid=(t[rt].l+t[rt].r)>>1;
int ans=0;
if(l<=mid) ans+=query(rt<<1,l,r);
if(r>=mid+1) ans+=query(rt<<1|1,l,r);
return ans;
}
我们可以发现这是一种中规中矩的写法,就是结构体建树,保存每个点左右儿子,权值和懒标记。
第二种
#include<bits/stdc++.h>
#define ll long long
#define lson rt<<1,l,mid
#define rson rt<<1|1,mid+1,r
using namespace std;
const int N=100000+10;
int a[N];
ll dat[N*4],add[N*4];
inline void build(int rt,int l,int r)
{
if(l==r)
{
dat[rt]=a[l];
return ;
}
int mid=(l+r)>>1;
build(lson);
build(rson);
dat[rt]=dat[rt<<1]+dat[rt<<1|1];
}
inline void spread(int rt,int l,int r)
{
//l,r 表示为 rt 的左右儿子
if(add[rt])
{
int mid=(l+r)>>1;
dat[rt<<1]+=(ll)add[rt]*(mid-l+1),add[rt<<1]+=add[rt];
dat[rt<<1|1]+=(ll)add[rt]*(r-mid),add[rt<<1|1]+=add[rt];
add[rt]=0;
}
}
inline void change(int rt,int l,int r,int L,int R,int k)
{
//l,r 表示为 rt 的左右儿子,下同
if(L<=l&&R>=r)
{
dat[rt]+=(ll)k*(r-l+1);
add[rt]+=k;
return ;
}
spread(rt,l,r);
int mid=(l+r)>>1;
if(L<=mid) change(lson,L,R,k);
if(R>=mid+1) change(rson,L,R,k);
dat[rt]=dat[rt<<1]+dat[rt<<1|1];
}
inline ll query(int rt,int l,int r,int L,int R)
{
if(L<=l&&R>=r)
{
return dat[rt];
}
spread(rt,l,r);
int mid=(l+r)>>1;
ll ans=0;
if(L<=mid) ans+=query(lson,L,R);
if(R>=mid+1) ans+=query(rson,L,R);
return ans;
}
int main()
{
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
build(1,1,n);
for(int i=1,opt,l,r,v;i<=m;i++)
{
scanf("%d%d%d",&opt,&l,&r);
if(opt==1) scanf("%d",&v),change(1,1,n,l,r,v);
else printf("%lld\n",query(1,1,n,l,r));
}
return 0;
}
第二种打法省去了左右儿子,而在函数中表现出来
虽然节省了空间,但参数变多了,容易在递归过程中爆栈,所以用 inline 优化(虽然好像没什么大用)
重链剖分
const int N=100000+10;
int head[N],ver[N*2],nex[N*2];
int dep[N],dfn[N],wson[N],size[N],top[N],fa[N];
void dfs1(int x)
{
dep[x]=dep[fa[x]]+1;
size[x]=1;
for(int i=head[x];i;i=nex[i])
{
int y=ver[i];
if(y==fa[x]) continue;
fa[y]=x;
dfs1(y);
size[x]+=size[y];
if(size[y]>size[wson[x]]) wson[x]=y;
}
}
void dfs2(int x,int nowtop)
{
dfn[x]=++num;
w[num]=a[x];
top[x]=nowtop;
if(wson[x]) dfs2(wson[x],nowtop);
for(int i=head[x];i;i=nex[i])
{
int y=ver[i];
if(y==fa[x]||y==wson[x]) continue;
dfs2(y,y);
}
}
我们发现在 dfs2 中,我们预处理了搜索序,使得树可以用线段树维护
那么,线段树和重链剖分就可以结合起来,计算树上信息统计问题
唯一一道例题:
题目描述
如题,已知一棵包含N个结点的树(连通且无环),每个节点上包含一个数值,需要支持以下操作:
操作1: 格式: 1 x y z 表示将树从x到y结点最短路径上所有节点的值都加上z
操作2: 格式: 2 x y 表示求树从x到y结点最短路径上所有节点的值之和
操作3: 格式: 3 x z 表示将以x为根节点的子树内所有节点值都加上z
操作4: 格式: 4 x 表示求以x为根节点的子树内所有节点值之和
输入格式
第一行包含4个正整数N、M、R、P,分别表示树的结点个数、操作个数、根节点序号和取模数(即所有的输出结果均对此取模)。
接下来一行包含N个非负整数,分别依次表示各个节点上初始的数值。
接下来N-1行每行包含两个整数x、y,表示点x和点y之间连有一条边(保证无环且连通)
接下来M行每行包含若干个正整数,每行表示一个操作,格式如下:
操作1: 1 x y z
操作2: 2 x y
操作3: 3 x z
操作4: 4 x
输出格式
输出包含若干行,分别依次表示每个操作2或操作4所得的结果(对P取模)
原题:
https://www.luogu.org/problem/P3384
分析:
一道模板题
我们可以发现,两点之间的路径可以用 lca 表达出来
如图: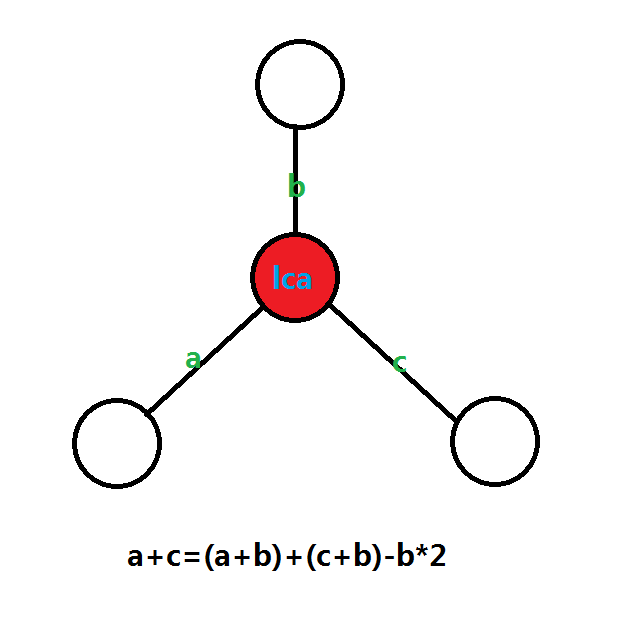
但是树上点到 lca 的距离不一定等于 线段树上 点到 lca 距离
那么我们就模拟一遍求 lca 的过程,把权值分段求出来
重链剖分求 lca 的实现步骤:
1) 将两点中链头更深的点跳到链头
2) 若两点不在同一重链上,更深点跳转到父节点
3) 重复操作 1)、2)直到两点处于同一条重链上,此时深度较浅的点即为所求
关于 3) 的证明:
很明显当两点处于同一条重链上时,它们的父节点也处于这条重链上,并且这个父节点,就是这两点中深度较浅的点。
代码
#include<bits/stdc++.h>
using namespace std;
const int N=100000+10;
int tot,num;
int n,m,r,p;
int w[N],a[N],dat[N*4],add[N*4];
int head[N],ver[N*2],nex[N*2];
int dep[N],dfn[N],wson[N],size[N],top[N],fa[N];
// 深度 搜索序 重儿子 子树大小 链头 父节点
inline void adde(int x,int y)
{
ver[++tot]=y;
nex[tot]=head[x];
head[x]=tot;
}
void dfs1(int x)
{
dep[x]=dep[fa[x]]+1;
size[x]=1;
for(int i=head[x];i;i=nex[i])
{
int y=ver[i];
if(y==fa[x]) continue;
fa[y]=x;
dfs1(y);
size[x]+=size[y];
if(size[y]>size[wson[x]]) wson[x]=y;
}
}
void dfs2(int x,int nowtop)
{
dfn[x]=++num;
w[num]=a[x];
//以搜索序重排权值
top[x]=nowtop;
if(wson[x]) dfs2(wson[x],nowtop);
for(int i=head[x];i;i=nex[i])
{
int y=ver[i];
if(y==fa[x]||y==wson[x]) continue;
dfs2(y,y);
}
}
inline void build(int rt,int l,int r)
{
if(l==r)
{
dat[rt]=w[l];
return ;
}
int mid=(l+r)>>1;
build(rt<<1,l,mid);
build(rt<<1|1,mid+1,r);
dat[rt]=dat[rt<<1]+dat[rt<<1|1];
dat[rt]%=p;
}
inline void spread(int rt,int l,int r)
{
if(add[rt])
{
int mid=(l+r)>>1;
dat[rt<<1]+=add[rt]*(mid-l+1),dat[rt<<1]%=p,add[rt<<1]+=add[rt];
dat[rt<<1|1]+=add[rt]*(r-mid),dat[rt<<1|1]%=p,add[rt<<1|1]+=add[rt];
add[rt]=0;
}
}
inline void change(int rt,int l,int r,int ls,int rs,int k)
{
if(l<=ls&&r>=rs)
{
dat[rt]+=k*(rs-ls+1);
dat[rt]%=p;
add[rt]+=k;
add[rt]%=p;
return ;
}
spread(rt,ls,rs);
int mid=(ls+rs)>>1;
if(l<=mid) change(rt<<1,l,r,ls,mid,k);
if(r>=mid+1) change(rt<<1|1,l,r,mid+1,rs,k);
dat[rt]=dat[rt<<1]+dat[rt<<1|1];
dat[rt]%=p;
}
inline int query(int rt,int l,int r,int ls,int rs)
{
if(l<=ls&&r>=rs)
{
return dat[rt];
}
spread(rt,ls,rs);
int mid=(ls+rs)>>1;
int ans=0;
if(l<=mid) ans+=query(rt<<1,l,r,ls,mid),ans%=p;
if(r>=mid+1) ans+=query(rt<<1|1,l,r,mid+1,rs),ans%=p;
return ans;
}
inline int qsum(int x,int y)
{
//两点间的修改
int ans=0;
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]]) swap(x,y);
ans+=query(1,dfn[top[x]],dfn[x],1,n);
ans%=p;
x=fa[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
ans+=query(1,dfn[x],dfn[y],1,n);
return ans%p;
}
inline void padd(int x,int y,int k)
{
//树上两点距离
k%=p;
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]]) swap(x,y);
change(1,dfn[top[x]],dfn[x],1,n,k);
x=fa[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
change(1,dfn[x],dfn[y],1,n,k);
}
inline int qson(int rt)
{
//由搜索序的特点可得,子树的搜索序一定比根大
return query(1,dfn[rt],dfn[rt]+size[rt]-1,1,n);
}
inline void sonadd(int rt,int k)
{
k%=p;
change(1,dfn[rt],dfn[rt]+size[rt]-1,1,n,k);
}
int main()
{
scanf("%d%d%d%d",&n,&m,&r,&p);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1,x,y;i<n;i++)
{
scanf("%d%d",&x,&y);
adde(x,y);
adde(y,x);
}
dfs1(r);
dfs2(r,r);
build(1,1,n);
//初始化
for(int i=1,opt,x,y,z;i<=m;i++)
{
scanf("%d",&opt);
if(opt==1)
{
scanf("%d%d%d",&x,&y,&z);
padd(x,y,z);
}else if(opt==2)
{
scanf("%d%d",&x,&y);
printf("%d\n",qsum(x,y));
}else if(opt==3)
{
scanf("%d%d",&x,&z);
sonadd(x,z);
}else
{
scanf("%d",&x);
printf("%d\n",qson(x));
}
}
return 0;
}
基于线段树有很多讲解,所以具体细节就不再详述了
至于树链剖分,可以看这里:
https://www.acwing.com/blog/content/350/


inline很难优化递归函数,避免递归爆栈的唯一方法是将栈变大。那该怎样将栈变大呢?
一般linux环境下默认的栈就够用了
好,谢谢