离散化

所谓离散化，就是当我们只关心数据的大小关系时，用排名代替原数据进行处理的一种预处理方法
当原数据很大或含有负数、小数时，难以表示为数组下标，一些算法和数据结构（如BIT）无法运作，这时我们就可以考虑将其离散化。

步骤：

*　将所有需要离散化的数据放到一个容器中（以下使用vector）；

*　排序，去重（可以手写，也可以用STL的algorithm库中的unique函数）；

*　要查询原数据在容器中的位置只需在容器中二分查找第一个大于等于该数据的数的位置

• 注意点：特别注意：由于使用到了前缀和，数组要下标从 1 开始计算，因此使用 STL 的 lower_bound() 查找二分查找左边界的时候，需要将返回值增加 1。

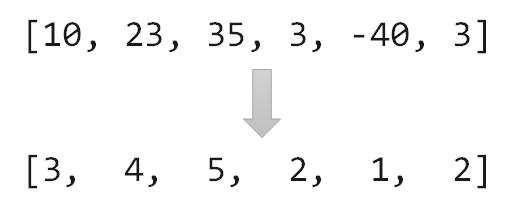
模板一：用$lower bound $ 实现(必要的时候记得 加 1)

vector<int> alls; // 存储所有待离散化的值
sort(alls.begin(), alls.end()); // 将所有值排序
alls.erase(unique(alls.begin(), alls.end()), alls.end());   // 去掉重复元素

// 二分求出x对应的离散化的值
int find(int x) // 找到第一个大于等于x的位置
{
     int a=alls.size()-1;
     return  lower_bound(alls,alls + a,x)-alls;

}

模板二：二分法

vector<int> alls; // 存储所有待离散化的值
sort(alls.begin(), alls.end()); // 将所有值排序
alls.erase(unique(alls.begin(), alls.end()), alls.end());   // 去掉重复元素

// 二分求出x对应的离散化的值
int find(int x) // 找到第一个大于等于x的位置
{
    int l = 0, r = alls.size() - 1;
    while (l < r)
    {
        int mid = l + r >> 1;
        if (alls[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return r + 1; // 映射到1, 2, ...n
}

题目表述 区间和 ：

假定有一个无限长的数轴，数轴上每个坐标上的数都是0。
现在，我们首先进行 n 次操作，每次操作将某一位置x上的数加c。
近下来，进行 m 次询问，每个询问包含两个整数 l 和 r ，你需要求出在区间 [l, r] 之间的所有数的和。

输入格式：

第一行包含两个整数n和m。
接下来 n 行，每行包含两个整数x和c。
再接下里 m 行，每行包含两个整数l和r。

输出格式：

共m行，每行输出一个询问中所求的区间内数字和。

数据范围：

−10^9 ≤ x ≤ 10^9,
1 ≤ n, m ≤ 10^5,
−10^9 ≤ l ≤ r ≤ 10^9,
−10000 ≤ c ≤ 10000

样例输入：

3 3
1 2
3 6
7 5
1 3
4 6
7 8

样例输出

8
0
5

分析

数据范围分析：

第一眼看到题目的时候，觉得题目好简单，就是一个标准的前缀和模板题。但是看到数据范围后，才发现好多坑。

1) 有一个无限长的数轴，数轴上每个坐标上的数都是 0。我们看到 x 的范围是 [−10^9, 10^9] ，也就是 2*10^9 大小，如果直接定义这么大的数组，估计要爆。

2) 实际操作的数据是 n，n 的范围是 [1, 10^5]，也就是进过了 n 次操作后，需要插入的数据包括 n 个坐标和 m 个 [l, r]，因此最多有 3*10^5 个数据是非零的，其他数据都是 0。310^5 对比 210^9，我们可以发现，非常符合离散化的前提。

3) 由于事前不知道 n 的大小，可以使用 C++ STL 中的 vector，而不是定义数组。

加入到 vector 后的数据如下，注意将所有的坐标加入到 vector 中

1 3 7 1 3 4 6 7 8

排序后的数据变为

1 1 3 3 4 6 7 7 8

去重后的数据变为

1 3 4 6 7 8

加法操作后，离散化后数据变为

0 2 6 0 0 5

离散化后前缀和为

0 2 8 8 8 13

完整代码：

#include <bits/stdc++.h>

using namespace std;

const int MAXN = 3e5+4;
int lsh[MAXN];//离散化后的数据
int sum[MAXN];//前缀和

int main() {
    int n,m,i;
    cin >> n >> m;

    vector<int> nums;//所有需要离散化数据
    vector<pair<int, int> > add;//加法操作
    vector<pair<int, int> > query;//查询操作
    //读入所有加法操作
    for (i=0; i<n; i++) {
        int x, c;
        cin >> x >> c;
        add.push_back({x, c});
        nums.push_back(x);//x需要离散化
    }
    //读入查询操作
    for (i=0; i<m; i++) {
        int l,r;
        cin >> l >> r;
        query.push_back({l, r});
        nums.push_back(l);
        nums.push_back(r);
    }

    //排序
    sort(nums.begin(), nums.end());
    //去重
    nums.erase(unique(nums.begin(), nums.end()), nums.end());// nums.erase(unique(nums),nums.end());

    //处理加法 (离散化)
    for (auto item:add) {
        int x = lower_bound(nums.begin(), nums.end(), item.first)-nums.begin()+1;//
        // int x = find(item.first);
        lsh[x]+=item.second;
    }

    //求前缀和
    for (i=1; i<=nums.size(); i++) {
        sum[i]=sum[i-1]+lsh[i];
    }

    //查询前缀和
    for (auto item:query) {
        int l = lower_bound(nums.begin(), nums.end(), item.first)-nums.begin()+1;
        int r = lower_bound(nums.begin(), nums.end(), item.second)-nums.begin()+1;
        cout << sum[r]-sum[l-1] << endl;
    }

    return 0;
}