链表 (单链表 / 双链表)
算法题目不适合采用结构体的链表实现方式, 采用数组模拟方式效率更快些,而且编码效率也更高些。 首先保存数据的肯定需要一个数组, 故有一个数组e用来保存数据作为节点的数据域, 由于要实现链表,故一个节点除了要保存数据域还要保存一个指针,用于指向其下一个节点。故用一个另外一个数组用于保存某个节点的下一节点的位置,数组下标索引为某个节点,其值为下一节点位置。
单链表练习链接 : 826. 单链表
#include<iostream>
using namespace std;
constexpr int N = 1e+5 + 10;
int n;
int e[N], ne[N], index, head;
// 链表初始化
auto init()
{
index = 0, head = -1;
}
// 头插法
auto push_front(int v)
{
e[index] = v;
ne[index] = head;
head = index++;
}
// 在第k个插入的数后面插入v
// 注意这里可能需要特判, 在第n个插入的数后面插入时候,传参传 n - 1
// 因为 index 是从0开始的, 故传参的位置需要进行 -1 处理
auto insert(int k, int v)
{
e[index] = v;
ne[index] = ne[k];
ne[k] = index++;
}
// 删除第k个插入的元素后面的元素
// 只是逻辑上的删除。 同样传参时注意 -1 的问题
auto del(int k)
{
ne[k] = ne[ne[k]];
}
双链表练习 : 827. 双链表
int n, index, head, tail;
int e[N], l[N], r[N]; // 双链表. e数组保存数据, l数组保存前驱. r数组保存后继
// 链表初始化
auto init()
{
// 0下标作为链表的左边界. 1下标表示链表右边界, 数据在逻辑上实现在他们之间进行插入
r[0] = 1; l[1] = 0;
index = 2; // 故 index 从2开始,故注意传参时位置下标 + 1
}
// 链表插入操作 --- 实现在第k个插入的数后面插入c
auto insert(int k, int c)
{
e[index] = c;
r[index] = r[k]; l[index] = k;
l[r[k]] = index; r[k] = index++;
}
// 链表中删除第k个元素 ----- 逻辑上删除
auto del(int k)
{
l[r[k]] = l[k];
r[l[k]] = r[k];
}
栈 & 队列
栈和队列只要记住其存储数据的特点为先进后出FILO 和 先进先出FIFO
算法实现上, 同样为了提高效率,采用数组模拟栈和队列的方式, 其实现代码如下:
栈数据结构的练习 : 模拟栈
队列数据结构的练习 : 模拟队列
// 栈的数据结构实现
constexpr int N = 1e+5 + 10;
int st[N], tt, n;
auto push(int x) { st[++tt] = x; } // 满堆栈的实现方式, tt指向的是当前栈顶元素,而不是空闲位置,故先++
auto pop() {--tt;} // 栈顶元素出栈
auto empty() -> bool { return tt == 0;} // 满堆栈的tt大小代表了栈的元素个数
auto query() -> int { return st[tt]; } // 返回栈顶元素
// 队列的数据结构实现
constexpr int N = 1e+5 + 10;
int n, front, back; // 队头,队尾, 初始状态 front == back 表示为空
int q[N];
auto push(int a) { q[back++] = a; } // 队尾插入元素, 队尾back为当前队列空闲位置的下标
auto pop() {front++;} // 出队, 将队头元素出队
auto empty() {return front == back;}
auto query() -> int { return q[front]; }
单调栈 & 单调队列
这里之前写过一些分析, 故直接跳转链接就好了。
单调栈和单调队列的分析 : 分析
KMP算法
KMP分析跳转链接 : KMP算法的理解
Trie树 — 字典树
Trie树,即字典树,又称单词查找树或键树,是一种树形结构,是一种哈希树的变种。典型应用是用于统计和排序大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。它的优点是:最大限度地减少无谓的字符串比较,查询效率比哈希表高。
Trie的核心思想是空间换时间。利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。
它有3个基本性质:
根节点不包含字符,除根节点外每一个节点都只包含一个字符。
从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串。
每个节点的所有子节点包含的字符都不相同。
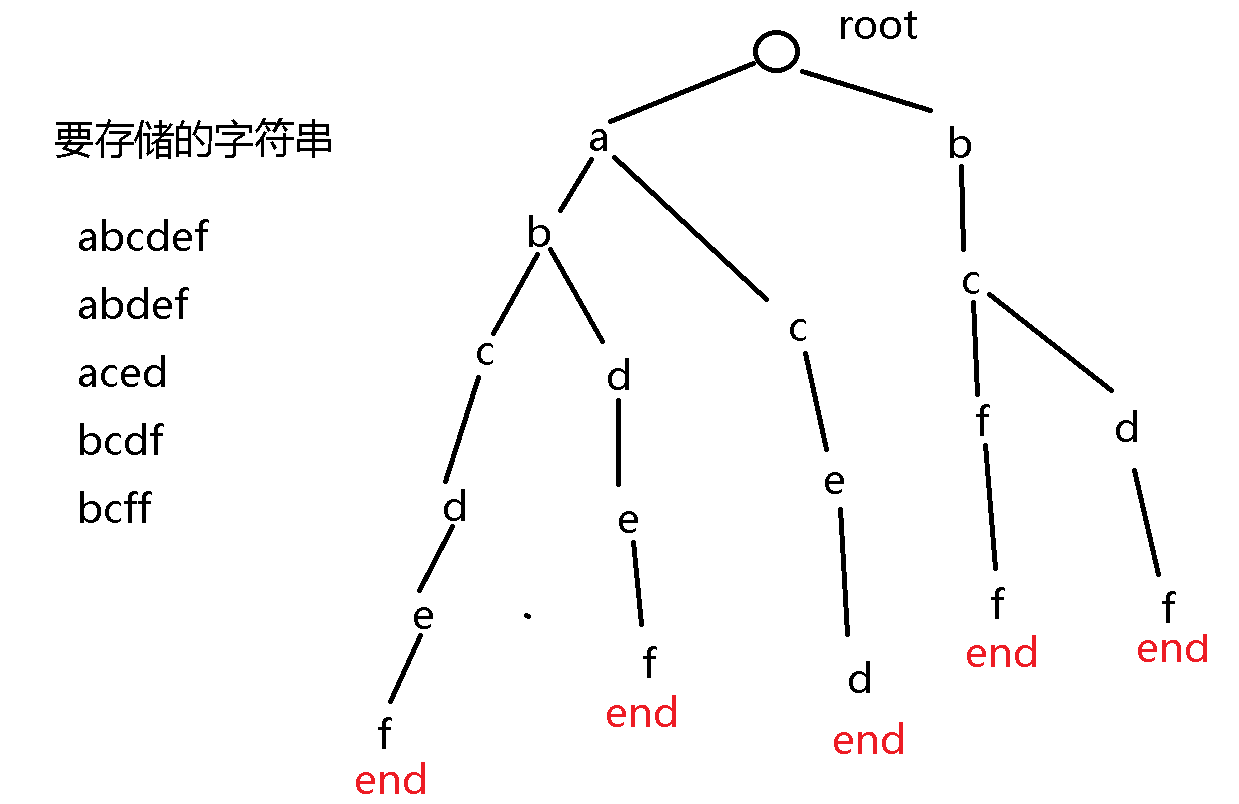
Tire树可以高效存储和查询字符串, 其中每个字符串都有一个结束标记,这个结束标记可以储存更多的信息,例如节点的个数之类的.
// 相关代码模拟
#include<iostream>
#include<string>
using namespace std;
constexpr int N = 1e+6;
int trie[N][26], cnt[N], idx; // idx用于指示现在用到了第几个节点,可以当作一个指针
// trie树的插入操作
auto insert(const char *str) // 往trie树加入一个字符串
{
int p = 0;
for(int i = 0; str[i]; ++i)
{
int t = str[i] - 'a';
if(!trie[p][t]) trie[p][t] = ++idx;
p = trie[p][t];
}
cnt[p]++; // cnt数组作为标记 end
}
// trie树的查询操作
auto find(const char *str)
{
int p = 0;
for(int i = 0; str[i]; ++i)
{
int t = str[i] - 'a';
if(!trie[p][t]) return 0;
p = trie[p][t];
}
return cnt[p]; // 若当前节点非空, 表示找到.
}
并查集
并查集是一种树型的数据结构,用于处理一些不相交集合(Disjoint Sets)的合并及查询问题。常常在使用中以森林来表示。
并查集简单说就是:初始化——合并——查找的一个过程。在不同的题目中,要求的点不一样。所以并查集就是要在不同的阶段,对新添加的变量做更新的一个过程。实现两个集合的合并,其原理是将集合中的一个元素作为该集合的代表元素,判断两个集合是否为同一集合只需判断其代表元素是否相等即可, 同样合并两个集合只需将其代表元素相同即可.
数组模拟并查集的核心 find()函数
int p[N]; // p[i] = k, 表示的是元素i所在集合的代表元素为k
auto find(int x) -> int // 并查集的核心 ----> 递归 + 路径压缩
{
if(p[x] != x) p[x] = find(p[x]);
return p[x];
}
// 合并操作 元素a所在的集合 和 元素b所在的集合合并
p[find(a)] = find(b);
// 判断两个元素是否在同一集合当中
if(find(a) == find(b))
// 在并查集操作中,除了用p数组保存每个元素其所在集合代表元素的信息用于实现集合的合并和查询外
// 经常需要保存一些其他的信息,这个时候可以再使用另外一个数组保存每个元素的额外信息
练习链接 : 合并集合 连通块中点的数量
练习链接 : 食物链 食物链问题的题解 : 食物链题解
堆的相关算法
关于堆之前也整理过了,这里直接跳链接 : 数据结构 – 堆
哈希表
散列表(Hash table,也叫哈希表),是根据关键码值(Key value)而直接进行访问的数据结构。也就是说,它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做散列函数,存放记录的数组叫做散列表。
在算法题目中常见的应用情景就是将一堆范围很大的数,映射到一个小的范围中去, 例如一堆数据的范围是0 ~ 10^9, 但这堆数据的个数并不多, 我们开不出一个10^9个int数据的栈空间的数组,但由于数据个数不多,我们只需开一小块空间,将这些大范围的数据映射到小空间即可。 在这个过程中映射的方式我们有一个函数h(x), h(x)的结果为x这个数在对应存储空间上的位置,这个函数叫做哈希函数。
由于数据的范围比较大,但是存储的空间比较小,故在映射的过程中就有可能存在冲突,即把两个不同的数字都映射到同一位置去了,故为解决这种冲突哈希表常用的存储方式有: (1) 开放寻址法 , (2) 拉链法
从一个例子来看这两种方法,例如将 -10^9 ~ 10^9 的一堆数,映射到小空间储存,这些数的个数不超过10^5
拉链法
首先一个一维数组用来保存哈希函数映射的位置,然后找到数组中的这个位置看是否为空,若不为空,则以该位置为头节点,用链表的方式插入一个数据,若不为空,则直接头插法插入即可,故总的来说就是一维数组的每个位置其实都对应有一条链表,该链表保存映射到该位置的数据。有邻接表的味道。
using namespace std;
const int N = 100003; // 取模的结果最好是一个质数,用于减少冲突的概率
int h[N], e[N], ne[N], idx; // h数组作为哈希函数映射的位置,e数组,ne数组, idx就是一个链表了
// 数据的插入
void insert(int x)
{
int k = (x % N + N) % N; // 这个就是哈希函数了,将x映射成一个较小的值,注意由于数据范围有负数,故这里+N处理
// 链表的头插法操作
e[idx] = x;
ne[idx] = h[k];
h[k] = idx ++ ;
}
// 数据查询操作
bool find(int x)
{
int k = (x % N + N) % N; // 查询x在h数组的映射位置
for (int i = h[k]; i != -1; i = ne[i]) // 遍历对应位置下的链表是否存在数据x
if (e[i] == x)
return true;
return false;
}
开放寻址法
开放寻址法只用到一个一维数组, 解决冲突的方式为若某个数据映射到的位置已经有数据了,则就找映射位置的下一个位置,判断是否有数据直到找到一个空位置,故开放寻址法所开辟的空间要足够大, 一般都开到题目的2 ~ 3 倍.
const int N = 200003, null = 0x3f3f3f3f;
int h[N];
int find(int x) // 开放寻址法的核心 ---> find函数找到一个位置
{
int t = (x % N + N) % N;
while (h[t] != null && h[t] != x) // 当不为空 或者 不等于x的时候循环++
{
t ++ ;
if (t == N) t = 0;
}
return t;
}
练习链接 : 模拟散列表
哈希表一种常见的应用情景 : 字符串哈希 ----> 将一个字符串映射成一个数字, 假如 A – 1, B – 2 这样子看的话, ABCD ------> 由哈希函数映射成 1234, 一般我们的应用场景是对字符串中的子串进行哈希,例如我们的字符串为 “aabbcd”, 那么h[1] = “a”,h[2] = “aa”, h[3] = “aab”, h[4] = “aabb”, h[5] = “aabbc”, h[6] = “aabbcd”, 现在我们要做的就是将h[1] ~ h[6] 由哈希函数映射成相对应的值,映射规则为将字符串作为一个p进制的数, 为防止这个数过大溢出,我们还要给它模上一个数。例如 “abcd” —> (d + c * p^1 + b * p^2 + a * p^3)% MOD.得到的结果即为字符串哈希得到的值
字符串哈希的方式我们一般通过经验值来避免冲突的发生,而不像前面的采用两种方法来解决映射冲突的问题. 一般P进制我们取 131 或者 13331, MOD 取 2^64(数据类型直接用unsigned long long 即可,溢出就相当于取模),采用这样的取法,在99.99%的情况下字符串哈希不会冲突(y总视频说的,wwwww). 故对于字符串 “xxxxxxxxxxx”, 我们想完成h[1] ~ h[n]的哈希值, 代码实现为
#include<iostream>
using namespace std;
constexpr int N = 1e+5 + 10, P = 131;
unsigned long long p[N], h[N];
char str[N];
for(int i = 1; i <= n; ++i)
{
cin >> str[i];
p[i] = p[i - 1] * P; // 这里顺便把 p^1 ~ p^n 先保存起来后面要用
h[i] = h[i - 1] * P + str[i]; // 计算 h[1] ~ h[n] 的哈希值
}
利用字符串哈希我们可以快速地判断在一个字符串中,可以快速判断其中两个子串是否, 只要比较子串的哈希值是否相同即可判断.

字符串哈希练习链接 : 841. 字符串哈希

