图论算法学习

作者： 作者的头像   zyyyds ,  2024-07-17 17:08:12 ,  所有人可见 ,  阅读 9

1


倍增LCA

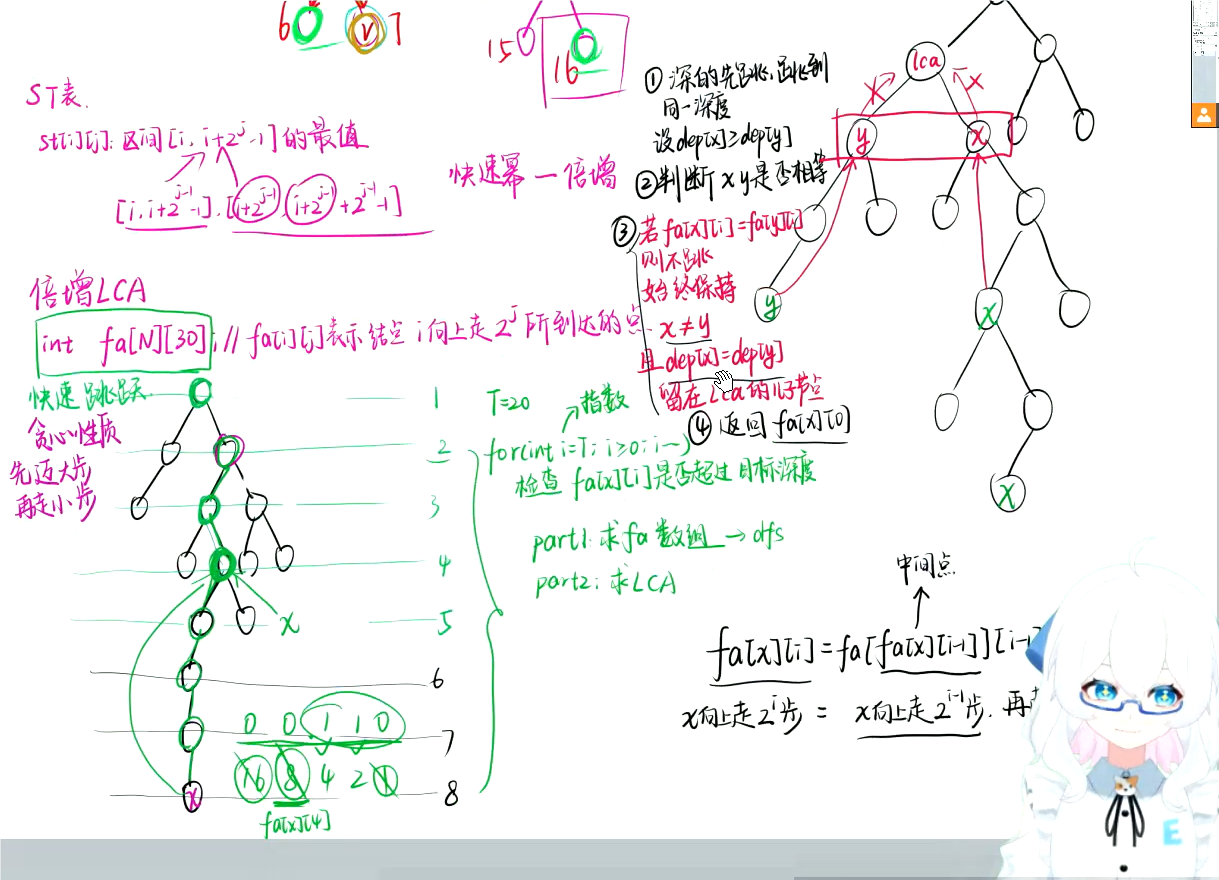
F7835268775CF6BF8717E4EA52F3C742.png

5F79D40561540A8AF5F89A9F6742A83C.png
Code

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 2e5 + 10, T = 20;
vector<int> g[N];

int fa[N][30], dep[N]; 
int n;

void dfs(int u)
{
    dep[u] = dep[fa[u][0]] + 1;

    for(int i = 1; i <= T; i ++) fa[u][i] = fa[fa[u][i - 1]][i - 1];

    for(auto &v : g[u])
    {
        dfs(v);
    }
}

int LCA(int u, int v)
{
   if(dep[u] < dep[v]) swap(u, v); //不妨设u的深度大于等于v的深度

   //跳跃，先走大步再走小步
   //将u点跳到与v相同的深度
   for(int i = T; i >= 0; i --) 
   if(dep[fa[u][i]] >= dep[v]) u = fa[u][i];

   if(u == v) return v;
   //一起往上跳 
   for(int i = T; i >= 0; i --)
   {
      if(fa[u][i] != fa[v][i]) 
      {
         u = fa[u][i];
         v = fa[v][i];  
      } 
   }

   return fa[u][0]; 
} 

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);

    cin >> n;

    for(int i = 2; i <= n; i ++)
    {
        int x;
        cin >> x;
        fa[i][0] = x;
        g[fa[i][0]].push_back(i); //g数组只存储子节点 
    } 

    dfs(1); //利用dfs来预处理深度和预处理fa数组

    int q;
    cin >> q;
    while(q --)
    {
      int u, v;
      cin >> u >> v;

      cout << LCA(u, v) << endl;    
    } 
    return 0;
}

Tarjan求强连通分量

991DEBC5BDD06A01CE8B8E82DCD6B699.png 

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;

const int N = 2e5 + 10, T = 20;

vector<int> g[N];

int dfn[N], low[N], idx, col[N], tot; //col为染色数组，tot代表颜色的总数 
int cnt[N]; 
bool ins[N]; //标记当前点是否在栈中 
int n, m;
stack<int> stk;
void targan(int x)
{
    //1.初始化dfn和low
    dfn[x] = low[x] = ++ idx;

    //2.入栈并标记

    stk.push(x);
    ins[x] = true;

    //3.遍历所有儿子

    for(auto &y : g[x])
    {
       if(!dfn[y]) //判断是否是回点 
       {
          targan(y);
          low[x] = min(low[x], low[y]);
       }
       else if(ins[y]) low[x] = min(low[x], dfn[y]); //这里注意要判断当前节点是否在栈中 
    } 

    //4.收拢，将该连通块染色并将其中的节点弹出栈 
    if(dfn[x] == low[x])
    {
       ++ tot;
       while(stk.size() && stk.top() != x)
       {
          col[stk.top()] = tot;
          cnt[tot] ++;
          ins[stk.top()] = false;
          stk.pop();    
       }

       col[x] = tot;
       cnt[tot] ++;
       ins[x] = false;
       stk.pop();
    } 
} 
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);

    cin >> n >> m;

    for(int i = 1; i <= m; i ++)
    {
        int a, b;
        cin >> a >> b;

        g[a].push_back(b);

    }

    for(int i = 1; i <= n; i ++)
    {
        if(!dfn[i]) targan(i);
    }

    vector<int> v;

    for(int i = 1; i <= tot; i ++) if(cnt[i] > 1) v.push_back(cnt[i]);

    if(v.size())
    {
        sort(v.begin(), v.end());
        for(auto &k : v) cout << k << " ";
    }
    else cout << -1 << endl;

    return 0;
}

targan求割点和割边

QQ_1721273331261.png
QQ_1721273350704.png

Code:

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;

const int N = 2e5 + 10, T = 20;

vector<int> g[N];

int n, m;
int cut, es; //cut为割点的数量，es为割边的数量

int dfn[N], low[N], idx;


void targan1(int x, int fa) //求割点函数 
{
    dfn[x] = low[x] = ++ idx;

    int child = 0;
    for(auto &y : g[x])
    {
        if(y == fa) continue;

        if(!dfn[y])
        {
            targan1(y, x);

            low[x] = min(low[x], low[y]);

            if(low[y] >= dfn[x]) child ++;
        }
        else low[x] = min(low[x], dfn[y]);
    }

    if((fa == 0 && child >= 2) || (fa != 0 && child >= 1)) cut ++; 
}

void targan2(int x, int fa) // 求割边函数 
{
    dfn[x] = low[x] = ++ idx;

    for(auto &y : g[x])
    {
        if(y == fa) continue;

        if(!dfn[y])
        {
            targan2(y, x);

            low[x] = min(low[x], low[y]);

            if(low[y] > dfn[x]) es ++;
        }
        else low[x] = min(low[x], dfn[y]);
    }
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);

    cin >> n >> m;

    for(int i = 1; i <= m; i ++)    
    {
        int a, b;
        cin >> a >> b;

        g[a].push_back(b);
        g[b].push_back(a);
    }

    for(int i = 1; i <= n; i ++)
    {
        if(!dfn[i]) targan1(i, 0); //求割点 
    }

    for(int i = 1; i <= n; i ++) dfn[i] = low[i] = 0;

    idx = 0;

    for(int i = 1; i <= n; i ++) 
    {
        if(!dfn[i]) targan2(i, 0);  
    }

    cout << cut << " " << es << endl; 

    return 0;
}

targan找环

QQ_1721289873416.png 

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2e5 + 9;

vector<int> g[N];

int dfn[N], low[N], idx, ans;
int stk[N], top;
bitset<N> ins;

void tarjan(int x, int fa)
{
    dfn[x] = low[x] = ++ idx;
    stk[++ top] = x;
    ins[x] = true;
    for(const auto &y : g[x]){
        if(y == fa)continue;

        if(!dfn[y])
        {
            tarjan(y, x);
            low[x] = min(low[x], low[y]);
        }else if(ins[x])low[x] = min(low[x], dfn[y]);
    }

    if(low[x] == dfn[x])
    {
        int cnt = 0;
        while(stk[top + 1] != x)
        {
            cnt ++;
            ins[stk[top --]] = false;
        }
        if(cnt > 1)
        {
            ans = cnt;
            return;
        }
    }

}

void solve()
{
    int n;cin >> n;
    for(int i = 1;i <= n; ++ i)
    {
        g[i].clear();
        stk[i] = dfn[i] = low[i] = 0;
        ins[i] = false;
    }
    stk[n + 1] = 0;
    ans = idx = top = 0;

    for(int i = 1;i <= n; ++ i)
    {
        int x, y;cin >> x >> y;
        g[x].push_back(y);
        g[y].push_back(x);
    }
    tarjan(1, 0);
    cout << ans << '\n';
}
int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int _;cin >> _;
    while(_ --)solve();
    return 0;
}

Bellman-Ford算法

QQ_1722331910323.png 

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;

const int N = 1e4 + 10, inf = 2e18;

struct edge{
    LL to, w;
};

vector<edge> g[N];

int n, m;
LL d[N];

void bellman_ford()
{
    for(int i = 2; i <= n; i ++) d[i] = inf;

    bool circle = false; //判断负环，最后一次出来之后还是true就是一直在更新，有负环
    for(int i = 1; i <= n; i ++)
    {
        circle = false;
        for(int x = 1; x <= n; x ++)
        {
            for(auto t : g[x])
            {
                if(d[t.to] > d[x] + t.w)
                {
                    d[t.to] = d[x] + t.w;
                    circle = true;
                }
            }
        }
    }

    if(circle) cout << "-1" << endl;
    else 
    {
        for(int i = 1; i <= n; i ++) cout << d[i] << " ";
    }
}
void solve()
{
   cin >> n >> m;

   for(int i = 1; i <= m; i ++)
   {
     int a, b, w;

     cin >> a >> b >> w;

     g[a].push_back({b, w});
   }

   bellman_ford(); 
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
     int T = 1;
     //cin >> T;
     while(T --)
     {
        solve();    
     }   
    return 0; 
}

spfa算法

QQ_1722334586560.png 

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;

const int N = 1e4 + 10, inf = 2e18;

struct edge{
    LL to, w;
};

vector<edge> g[N];

int n, m;
LL d[N];
bool inq[N]; //判断是否在队列中 
int cnt[N]; // 判断是否存在负环 
bool spfa(int st)
{
    for(int i = 1; i <= n; i ++) d[i] = inf;
    d[st] = 0;
    queue<int> q;

    q.push(st);
    inq[st] = true;

    while(q.size())
    {
        int t = q.front();
        q.pop();

        for(auto &v : g[t])
        {
            if(d[v.to] > d[t] + v.w)
            {
                ++ cnt[v.to];
                if(cnt[v.to] >= n) return true; //判断存在负环 

                d[v.to] = d[t] + v.w;

                if(!inq[v.to]) q.push(v.to);
            }
        }
    }
    return false;
}
void solve()
{
   cin >> n >> m;

   for(int i = 1; i <= m; i ++)
   {
     int a, b, w;

     cin >> a >> b >> w;

     g[a].push_back({b, w});
   }

   bool flag = spfa(1);

   if(flag) cout << "-1" << endl;
   else 
   {
      for(int i = 1; i <= n; i ++)
      {
          cout << d[i] << " ";  
      } 
   } 
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
     int T = 1;
     //cin >> T;
     while(T --)
     {
        solve();    
     }   
    return 0; 
}

差分约束系统

QQ_1722396247900.png
QQ_1722396267093.png 

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;

const int N = 5e3 + 10, inf = 2e18;

struct edge{
    LL to, w;
};

vector<edge> g[N];

int n, m;
int cnt[N];
LL d[N];
bool inq[N];
bool spfa(int st)
{
    queue<int> q;
    for(int i = 1; i <= n; i ++) d[i] = inf;
    memset(inq, false, sizeof inq);
    memset(cnt, 0, sizeof cnt);
    d[st] = 0;
    q.push(st);
    inq[st] = true;

    while(q.size())
    {
       int x = q.front();
       q.pop();
       inq[x] = false;

       for(auto &v : g[x])
       {
           if(d[v.to] > d[x] + v.w)
           {
               //判断是否存在负环，这里要判断n + 1因为多加了一个虚拟源点 
               if(++ cnt[v.to] >= n + 1) return false;

               d[v.to] = d[x] + v.w;

               if(!inq[v.to]) 
               {
                q.push(v.to); 
                inq[v.to] = true;
               }
           }    
       }    
    } 
    return true;    
}
void solve()
{
    cin >> n >> m;

    for(int i = 0; i <= n; i ++) g[i].clear();

    for(int i = 1; i <= m; i ++)
    {
        int op;
        cin >> op;

        if(op == 1)
        {
           int x, y, z;
           cin >> x >> y >> z;

           g[y].push_back({x, z});  
        }
        else if(op == 2)
        {
            int x, y, z;
            cin >> x >> y >> z;

            g[x].push_back({y, -z});
        }
        else
        {
            int x, y;
            cin >> x >> y;

            g[x].push_back({y, 0});
            g[y].push_back({x, 0});
        }
    }

    for(int i = 1; i <= n; i ++) g[0].push_back({i, 0}); //建立虚拟源点 

    if(spfa(0)) // 如果存在负环则无解 
    {
        cout << "YES" << endl;
    }
    else cout << "NO" << endl;
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
     int T = 1;
     cin >> T;
     while(T --)
     {
        solve();    
     }   
    return 0; 
}

染色法判定二分图

QQ_1722409461517.png 

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;

const int N = 2e5 + 10, inf = 2e18;

vector<int> g[N];

int col[N];
int n, m;

bool dfs(int x, int c)
{
    col[x] = c;

    for(auto &y : g[x])
    {
        if(!col[y])
        {
            if(!dfs(y, 3 - c)) return false;
        }
        else if(col[y] == col[x]) return false;
    }

    return true;
}

void solve()
{
    cin >> n >> m;

    for(int i = 1; i <= m; i ++)
    {
        int a, b;
        cin >> a >> b;

        g[a].push_back(b);
        g[b].push_back(a);
    }  

    bool ans = true;
    for(int i = 1; i <= n; i ++)
    {
         if(!col[i])
         {
             if(!dfs(i, 1))
             {
               ans = false;
               break;   
             }
         }  
    }

    if(ans) cout << "YES" << endl;
    else cout << "NO" << endl; 
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
     int T = 1;
    // cin >> T;
     while(T --)
     {
        solve();    
     }   
    return 0; 
}

二分图的最大匹配

原理解析 

#include<iostream>
#include <cstring>
#include<algorithm>
using namespace std;
// 邻接表存储图
int n1, n2, m;
int h[500], e[100010],ne[100010], idx = 0;
//st 标记是否递归找过， match[x]：和 x 编号的男生的编号
int st[510], match[510];
//存图函数
void add(int a, int b){
    e[idx] = b, ne[idx] = h[a]; h[a] = idx++;
}
//递归找可以匹配的点
bool find(int x){
    // 和各个点尝试能否匹配
    for(int i = h[x]; i != -1; i = ne[i]){
        int b = e[i];
        if(!st[b]){//打标记
            st[b] = 1;
            // 当前尝试点没有被匹配或者和当前尝试点匹配的那个点可以换另一个匹配
            if(match[b] == 0 || find(match[b])){
                // 和当前尝试点匹配在一起
                match[b] = x;
                return true;
            }
        }
    }
    return false;
}

int main(){
    memset(h, -1, sizeof h);
    cin >> n1 >> n2 >> m;
    // 保存图，因为只从一遍找另一边，所以该无向图只需要存储一个方向
    for(int i = 0; i < m; i++){
        int a, b;
        cin >> a >> b;
        add(a, b);
    }
    int res = 0;
    //为各个点找匹配
    for(int i = 1; i <= n1; i++){
        memset(st, 0, sizeof st);
        //找到匹配
        if(find(i)) res++;
    }
    cout << res;
    return 0;
}

0 评论