题目全部来自于 LeetCode的简单题 ，然后第三题没考虑到下标为负对数组无意义，但当时在acwing 上还是oj出了像样的结果，可能是不同编译器的原因。
可以考虑将j下标右移来使下标合法。

今年复旦的三道题相当简单，可能是开卷的原因。推测对复试结果的影响应该不大
不确定对不对

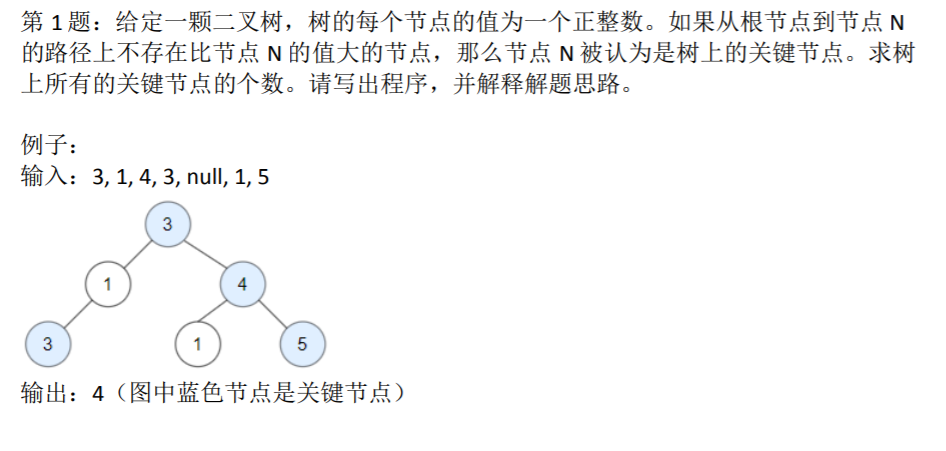
考点：数组模拟二叉树
我们可以用一个数组 a[ ] 来模拟这个完全二叉树，下标从 1 开始 ；
对于下标为 i 的结点，其 左孩子下标为 2i,右孩子为 2i + 1;
利用这个性质先读入二叉树，再顺序遍历这个数组 ；
如果当前结点大于等于父节点，cnt++；
否则更新该结点的值为其父节点的值；

#include<iostream>
#include<string>
using namespace std;
const int N=10010;
int tree[N],idx=1;

int main()
{
     string a;
     while(cin>>a)
     {
         if(a=="null")  
         {
             continue;
             idx++;
         }

         int x=stoi(a);
         tree[idx++]=x;
     }

     int ans=0;
     for(int i=1;i<idx;i++)
     {
         if(tree[i]>=tree[i/2])   ans++;
         else  tree[i]=tree[i/2];
     }

     cout<<ans<<endl;
     return 0;
}

考点： dp 问题；
到达第 i 个台阶的最后一步一共有两种情况，（两步或者一步）
写出状态转移方程： f[i]=f[i-1]+f[i-2]
确定初始状态 ： f[1]=1,f[2]=2;
从 3 开始 维护结果数组 f[]
时间复杂度 O(N) ；

#include<iostream>
using namespace std;
const int N=100100;
long long  f[N];


int main()
{
    int n;
    cin>>n;

    f[1]=1,f[2]=2;

    for(int i=3;i<=n;i++)
       f[i]=f[i-1]+f[i-2];
    cout<<f[n]<<endl;
    return 0;
}

考点：还是 Dp 问题
f[i][j] 表示 对于序列的前 i 个数，取得期望值 j 的方法的总数；
类似上一题，讨论第 i 个数 的取法，可以有 取正 和 取负 两种状态；
写出状态转移方程： f[i][j]=f[i-1][j-a[i]]+f[i-1][j+a[i]]
初始状态： f[1][a[1]]=1,f[1][-1*a[1]]=1;
注意 j 在转态转移过程中会取到负值，故过程中 j 从 -sum 维护到 +sum；
优化方法：滚动数组优化，降低空间复杂度
时间复杂度 O(N^2)

#include<iostream>
using namespace std;
const int N=10010;
int f[N][N];
int a[N],idx=1;
int sum;
int E;
int main()
{
    cin>>E;
    while(cin>>a[idx])
        sum+=a[idx++];       

    f[1][a[1]]=1,f[1][-1*a[1]]=1;

    for(int i=2;i<idx;i++)
    {
        for(int j=-1*sum;j<=sum;j++)
        {
            f[i][j]=f[i-1][j-a[i]]+f[i-1][j+a[i]];
        }
    }

    cout<<f[idx-1][E]<<endl;
    return 0;
}