1.nim博弈

题目：
给定 n堆石子，两位玩家轮流操作，每次操作可以从任意一堆石子中拿走任意数量的石子（可以拿完，但不能不拿），最后无法进行操作的人视为失败。

分析：（下面所说的状态都是针对于先手）
假设现在有三堆石子。（0，0，0）为一种必败状态；（0，2，2）为一种必败状态，先手无论怎么拿后手都与先手拿相同的数量；（1，2，3）为必败状态，无论先手怎么拿，后手都可以让当前的局势变为列举的第二种状态。因为（0，0，0）是最终状态，石子总数只会逐渐变小，后手的优先策略为始终保持m[1]^m[2]^…^m[i-1]^m[i]为0，所以一定会走到（0，0，0）这一局势。

规律：必败状态的充要条件是m[1]^m[2]^…^m[i-1]^m[i]=0。

当m[1]^m[2]^…^m[i-1]^m[i]！=0时，先手一定可以通过某种方式使得m[1]^m[2]^…^m[i-1]^m[i]变为0。
证明：当前m[1]^m[2]^…^m[i-1]^m[i]=x，x最高位在第k位置，a1~ai
中一定至少存在一个第k位置为1，设这个数为aj，aj^x<aj（因为第k位置由1变成0了），所以只需要拿取aj-（aj^x）个石子，这样会使得aj变为aj^x;
如果当前先手面对的是m[1]^m[2]^…^m[i-1]^m[i]=0，无论怎么拿取m[1]^m[2]^…^m[i-1]^m[i]都不会变成0；
证明：假设初始m[1]^m[2]^…^m[i-1]^m[i]=0，反证，如果拿取后m[1]^m[2]^..^m[j]^..^m[i-1]^m[i]=0,那么m[j]=m[j],因为不能不拿所以矛盾

2.台阶nim游戏

题目：
现在，有一个 n级台阶的楼梯，每级台阶上都有若干个石子，其中第i级台阶上有ai个石子(i≥1)。两位玩家轮流操作，每次操作可以从任意一级台阶上拿若干个石子放到下一级台阶中（不能不拿）。已经拿到地面上的石子不能再拿，最后无法进行操作的人视为失败。

分析：
先手的拿取可以分为两种，a：拿偶数台阶上的数，b:拿取奇数台阶上的数。
当选择为a时，假设先手从第4台阶上拿取了m个到第3台阶上，后手就会把这m个石子放到第2台阶上，后手要始终保持奇数台阶上的石子数量保持不变
当选择为b时候，假设先手从第3台阶拿了m个到第2台阶，后手需要把这m个石子从第2台阶拿到第1台阶；假设先手从第2台阶拿取m个到第1台阶，先手就需要把这m个石子拿到地上。

规律：初始m[1]^m[2]^…^m[i-1]^m[i]=0时，后手一定有方法维护这个式子的结果为0，使先手面对必败状态，最终面对（0，0，0）状态，先手必败

3.集合nim博弈

题目：给定 n堆石子以及一个由 k个不同正整数构成的数字集合S。现在有两位玩家轮流操作，每次操作可以从任意一堆石子中拿取石子，每次拿取的石子数量必须包含于集合 S，最后无法进行操作的人视为失败。

sg函数：
在博弈问题中，每一种状态可以称之为当前的局势，局势的变化可以由图表示出来，如

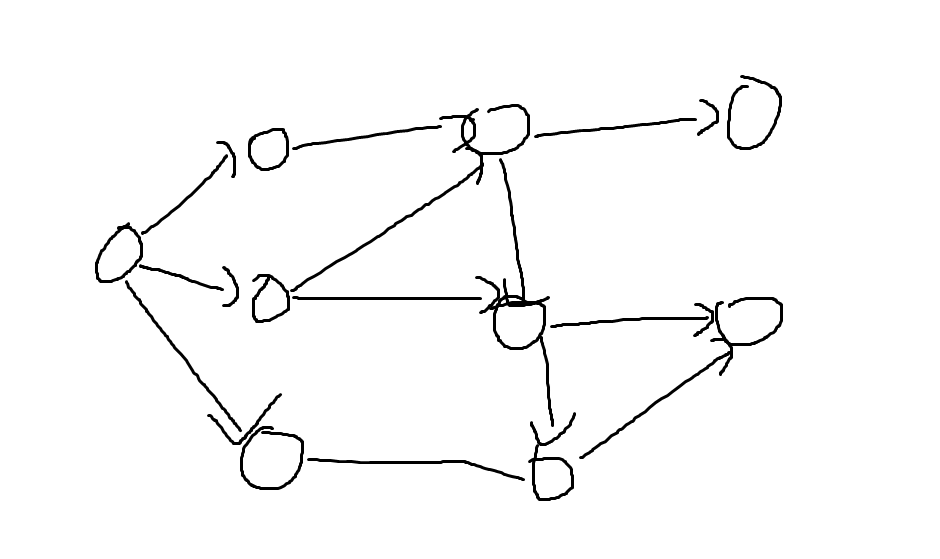
sg函数的含义：设必败状态的函数值为0，当前局势的sg函数为该局势除去可以转变局势的sg值以外最小的自然数，例如：

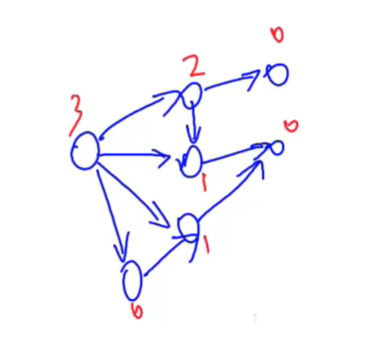
上述的图不止有一个，有几堆就会有几个

规律：起始所有局势的sg值异或的结果为0先手必败。
如果所有局势sg函数值都为0，那么异或结果为0。
假设当前异或为x，一定存在一个sg[i]^x<sg[i],由sg函数的性质可知，如果当前局势为sg值为x，那么一定可以走到sg值小于x的任意一个局势，这里走到sg值为sg[i]^x的局势，使得sor的值为0

分析：如果起初先手面对所有局势的sg值异或的结果不为0，假设当前只有一个图，先手无论怎么走后手一定可以让先手面对的局势的sg值不为0（图中可看出）