word编码

对一个词的向量表示，让计算机便于处理的方法，主要就有两种：
1. 离散化表示：如独热编码
2. 分布式表示：将词的含义映射到高维度的向量上

我们都知道，独热编码的好处是可解释强，且比较清晰简单，很容易构建，但缺点同样明显，就是不可扩展，需要巨大的维度，且无法表示词与词之间的相似度问题，因为任意两个向量都是正交的。

对应的解决办法就是

we encode similarity in real value vector. — distributional semantics

核心：一个词的意思往往是由它附近的词给出的。

以银行“banking”为例：

我们将上下文出现的单词视为实值高维度向量，每个向量一定程度上代表词的含义和词的表达方式，称为词向量（word vector），词嵌入（word embedding）

这种表示方法是分布式表示，而不是本地化表示，原因就是将单词的含义分布在了向量的每一个维度上（如512等）

现在正式引入Word2vec的工作（2013）：

我们现在有一堆文本需要处理，称为语料库corpus，我们经过预处理，如停用词处理后，为每个单词建立比较好的词向量。

在文本中，每个位置的词都有一个中心词c和周边词o。对于每一个给定的中心词c，计算周边词o的概率，并不断进行中心词的变化，调整概率进行最大化。

以下面的一段文本为例：

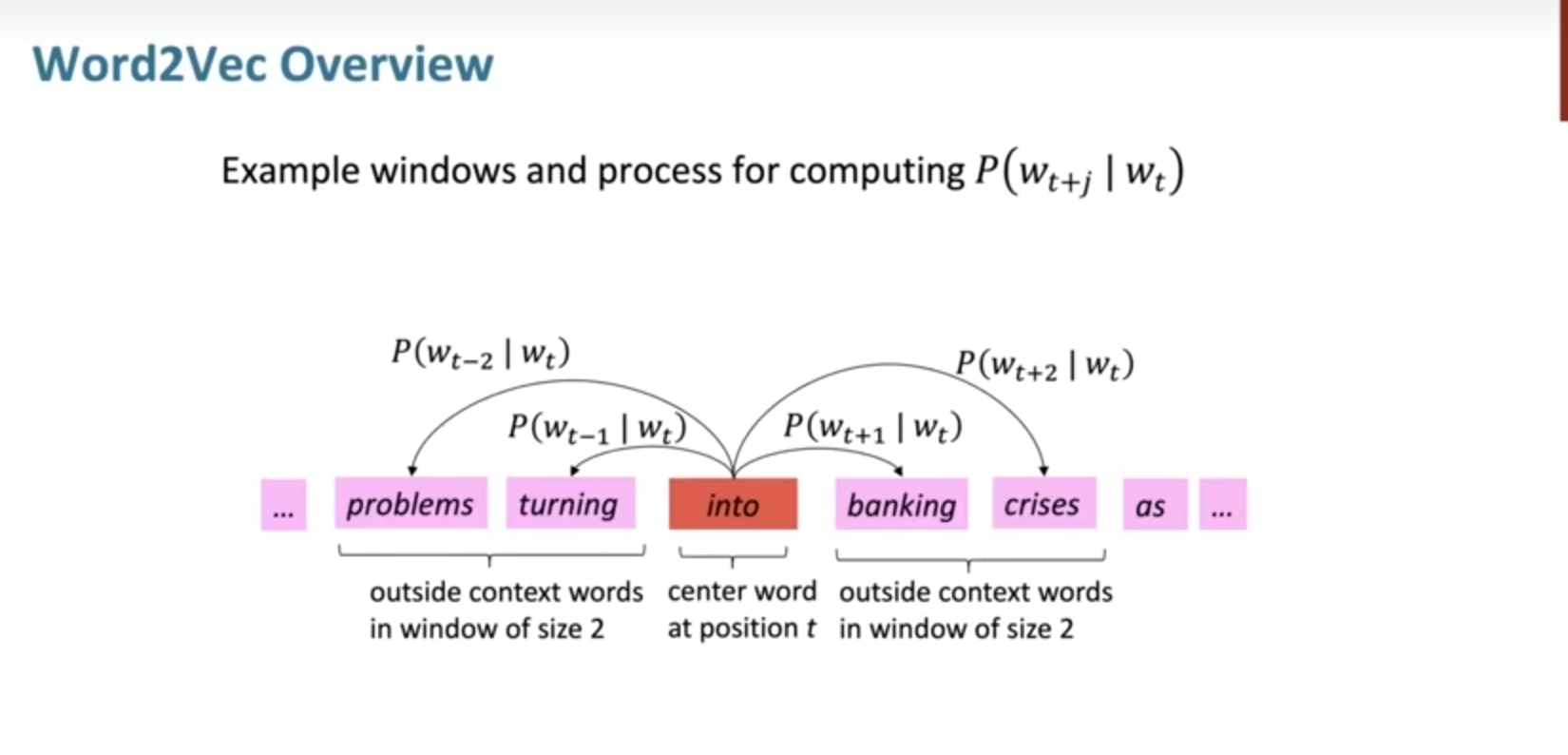
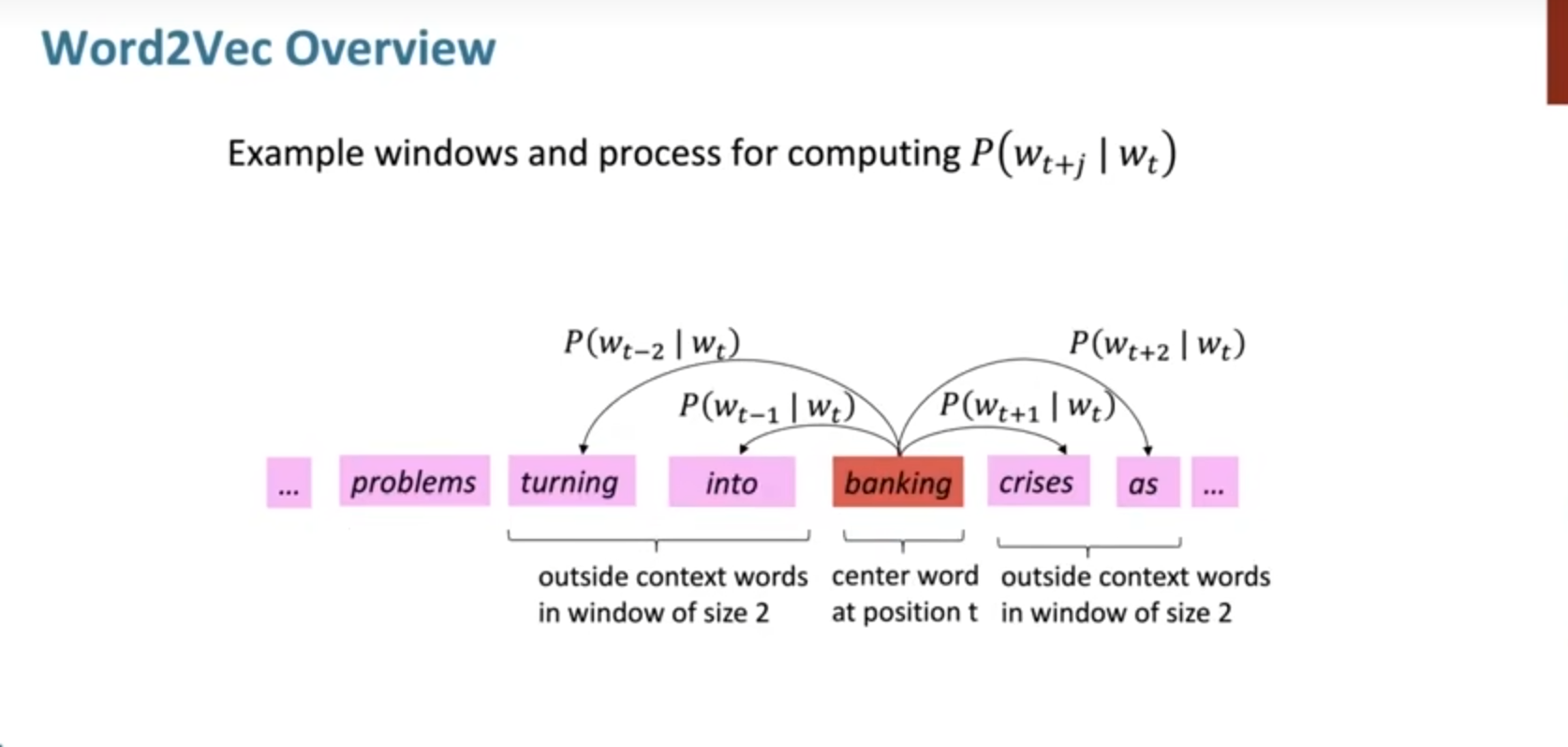
那么核心问题来了，我们如何计算一个词在中心词的上下文中出现的概率？

对应每个位置，我们都在一个窗口大小size内预测上下文出现的概率，并将每一个位置作为中心词的情况进行乘积，其实是极大似然估计的思想。之后建立损失函数，为了比较好处理乘积的情况，我们使用负对数的技巧，这样乘积就可以变为加和。

在Word2vec中，每一个单独的条件概率的计算为：中心词c与周边词o的点乘，再过一个softmax函数进行归一化得出。

$$ P(O=o\mid C=c)=\frac{\exp(\boldsymbol{u}_o^\top\boldsymbol{v}_c)}{\sum_{w\in\mathrm{Vocab}}\exp(\boldsymbol{u}_w^\top\boldsymbol{v}_c)} $$

其实这里我们根据以上的思想和计算过程也知道了，每一个词实际上是有两个向量进行表示的，分别是这个词作为中心词center的时候和作为周边词context的时候。

单独的条件概率我们看完了，接下来就是整体的似然概率了，那就是条件概率的连乘积形式。

$$ L(\theta)=\prod_{t=1}^T\prod_{-m\leq j\leq m}P(w_{t+j}\mid w_t;\theta) $$

那么目标函数（损失函数）就是可以先求个对数将乘积的形式转化为加和的形式，再取个平均和加个符号，就是标准的最小化损失函数的形式。

$$ J(\theta)=-\frac1T\log L(\theta)=-\frac1T\sum_{t=1}^T\sum_{-m\leq j\leq m}\log P(w_{t+j}|w_t;\theta) $$

整个的计算过程如下图比较清晰简单给出：

可以看到这时候已经具备了模型的全部组成部分，接下来就该训练优化了：

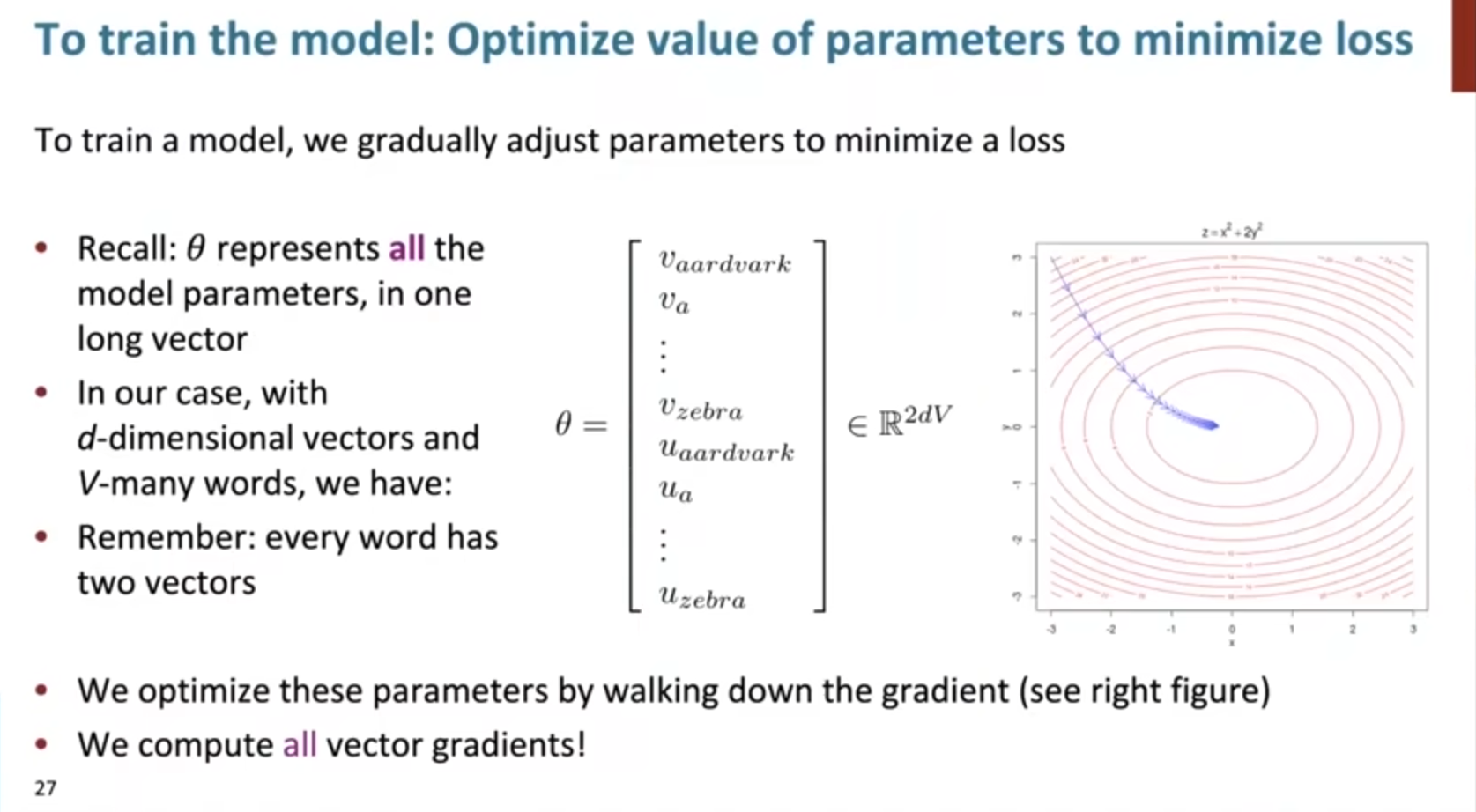
具体的计算推导，还是要手搓一遍比较舒服！

这里稍微注意一下即可：

对于每个词而言，同时会有中心向量center vector和上下文向量contex vector，因此需要分别求偏导进行优化，但都类似。

优化的过程使用梯度下降法gradient descent。初始化后，设计好学习率和训练轮次，进行迭代即可。

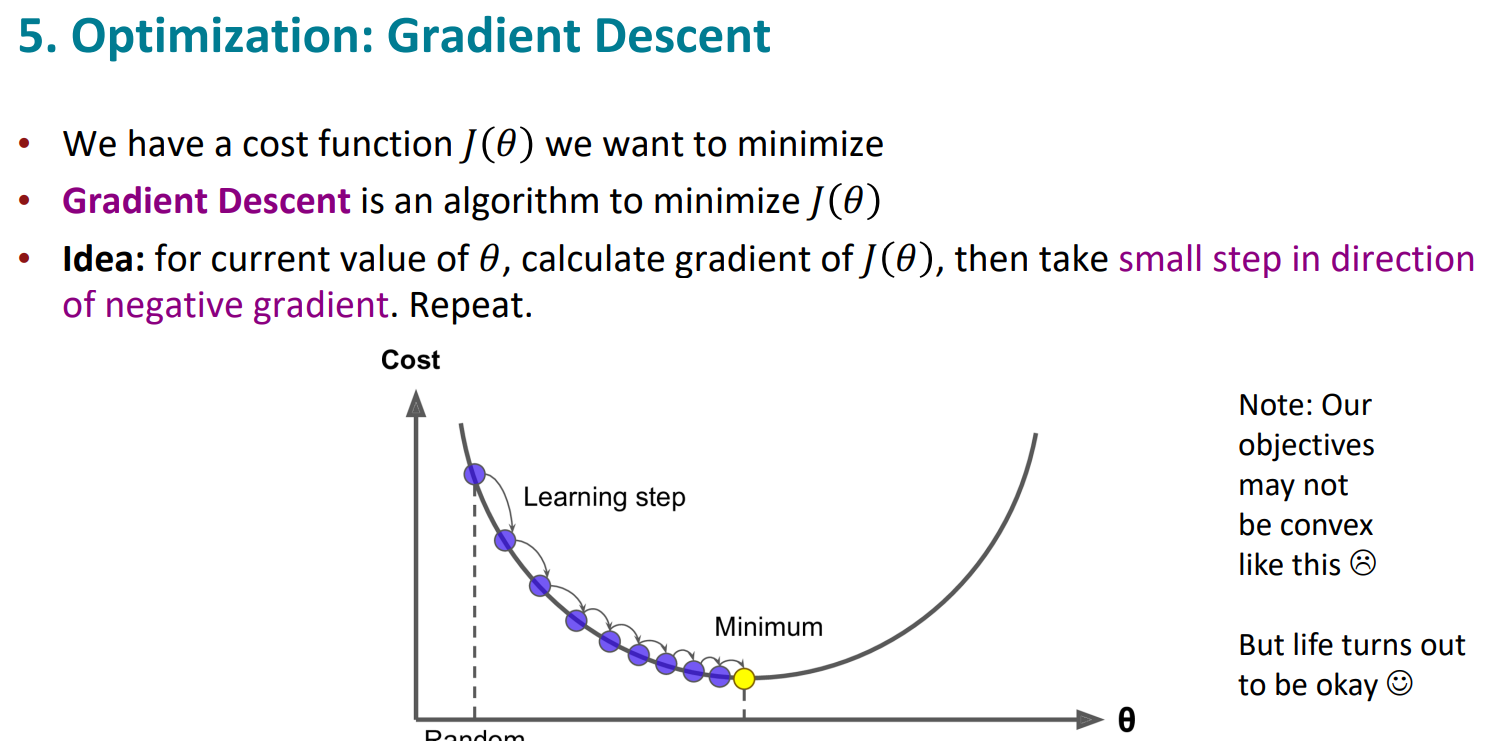
while True:
    theta_grad = evaluate_gradient(J,corpus,theta)
    theta = theta-alpha*theta_grad

$$\theta^{new}=\theta^{old}-\alpha\nabla_\theta J(\theta)$$

$$\theta_j^{new}=\theta_j^{old}-\alpha\frac{\partial}{\partial\theta_j^{old}}J(\theta)$$

这是梯度下降，每次更新梯度是对所有样本都进行，但如果是这样计算，将会非常浪费时间。

梯度下降使用整个训练数据集来计算梯度，因此它有时也被称为批量梯度下降

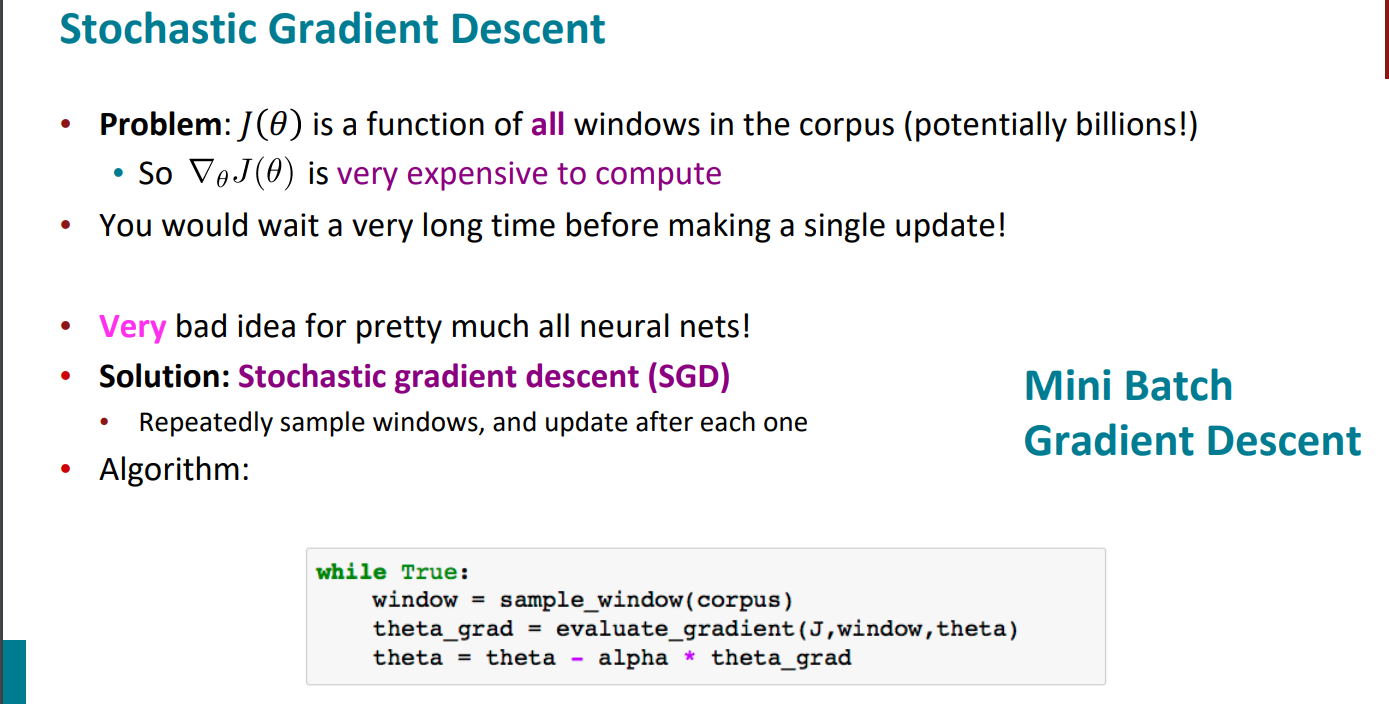
因此，为了计算复杂度的下降需求，我们可以随机梯度下降（Stochastic gradient descent，SGD）
，也就是在每次更新时用1个样本。但这样带来的问题也是显而易见的，就是随机性太强，容易带来很多噪声，会出现局部极值的情况。

因此，既不想每次更新梯度都需要全部样本的参与，因为这样开销实在太大，时间成本太高，但也不想每次更新梯度就只有一个样本参与，这样随机性过强，有时候很难向着最优的方向去走，那么就有一个折中的方法，mini-batch梯度下降（Mini Batch Gradient Descent）

mini-batch梯度下降在每次更新时用b个样本,其实批量的梯度下降就是一种折中的方法，他用了一些小样本来近似全部的，其本质就是我1个指不定不太准，那我用个30个50个样本那比随机的要准不少了吧，而且批量的话还是非常可以反映样本的一个分布情况的。在深度学习中，这种方法用的是最多的，因为这个方法收敛也不会很慢，收敛的局部最优也是更多的可以接受！

def mini_batch_gradient_descent(X, y, theta, compute_gradient, learning_rate=0.01, batch_size=32, epochs=100):
    """
    实现mini-batch梯度下降算法。

    参数：
    X : numpy.ndarray
        输入特征矩阵，形状为 (样本数量, 特征数量)。
    y : numpy.ndarray
        目标标签向量，形状为 (样本数量, 1)。
    theta : numpy.ndarray
        需要优化的参数向量，形状为 (特征数量, 1)。
    compute_gradient : function
        计算梯度的函数，输入为 (theta, X_batch, y_batch)，输出为梯度。
    learning_rate : float, 可选
        学习率，默认值为 0.01。
    batch_size : int, 可选
        每个mini-batch的大小，默认值为 32。
    epochs : int, 可选
        训练的轮数，默认值为 100。

    返回：
    numpy.ndarray
        优化后的参数向量 theta。
    """
    m = X.shape[0]  # 样本数量
    n_batches = m // batch_size  # mini-batch的数量

    for epoch in range(epochs):
        indices = np.arange(m)  # 创建索引数组
        np.random.shuffle(indices)  # 随机打乱索引数组

        for batch in range(n_batches):
            # 获取当前mini-batch的索引
            batch_indices = indices[batch * batch_size:(batch + 1) * batch_size]
            # 根据索引获取mini-batch的数据
            X_batch = X[batch_indices]
            y_batch = y[batch_indices]

            # 计算当前mini-batch的梯度
            grad = compute_gradient(theta, X_batch, y_batch)
            # 更新参数 theta
            theta -= learning_rate * grad

    return theta  # 返回优化后的参数

参考

https://web.stanford.edu/class/cs224n/
http://bitjoy.net/category/0%e5%92%8c1/stanford-cs224n-nlp-with-deep-learning/
https://www.bilibili.com/video/BV1d6421f7oW/?spm_id_from=333.337.search-card.all.click&vd_source=de334f24ee86583df2785811808ca76b