再回顾一下Word2vec的核心思想和计算过程:
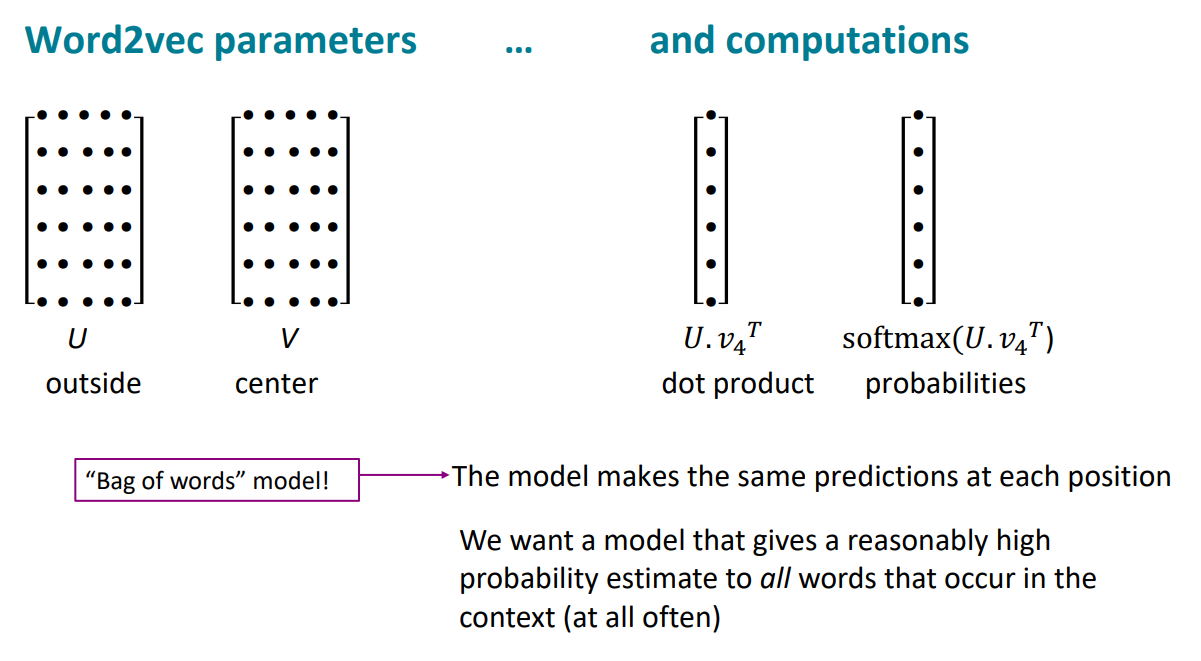
这里出现了一个传统NLP的名词:词袋模型(bag of words),那就停下脚步去了解一下
词袋模型的基本概念便是将每个文档视为无序词汇集,只考虑每个词语的出现频率,将出现频率作为文本的特征地图。虽然这是一种简单的理念和思路,但在实践中仍然可能是有效的选择。
从定义上我们就很容易看出词袋模型的特点,那就是我们只是考虑词在词汇表中出现的频率次数,二忽略了顺序问题,每个文档被转换为一个向量,其中每个元素代表字典中的一个词汇,并记录该词在文档中出现的次数。
除了顺序问题,那就是词与词之间没有优先级和重要性的区别,这个就很难受。
那么还有一个问题也很难受,就是多义词问题根本无法解决,因为star到底是星星还是明星,都是star,没有语境信息的利用。
(好了,我们回来)
这里我们需要关注word2vec的更多细节部分:
论文实际提出了两种模型,一种是根据中心词预测周边,一个是根据周边预测中心,实践表明,根据中心预测上下文的这个模型思路更好。
现在我们在模型训练过程中用的是朴素的softmax,比较简单易懂。但当训练集的语料库非常庞大的时候,每一次的预测都需要基于全部的数据集进行计算,这将会是一个巨大的时间开销。因此,文章中提出了两个优化的训练方式,这个我将再之后详细阅读论文的时候,再专门写,这里先初步明确一下:
- Hierarchical softmax:层次sotfmax
- Negative Sampling:负采样

这里去看了原论文,没有详细讲层次sortmax和负采样的情况,只是一带而过。就去搞明白这块儿吧

让我们看一下skip-gram的模型架构:
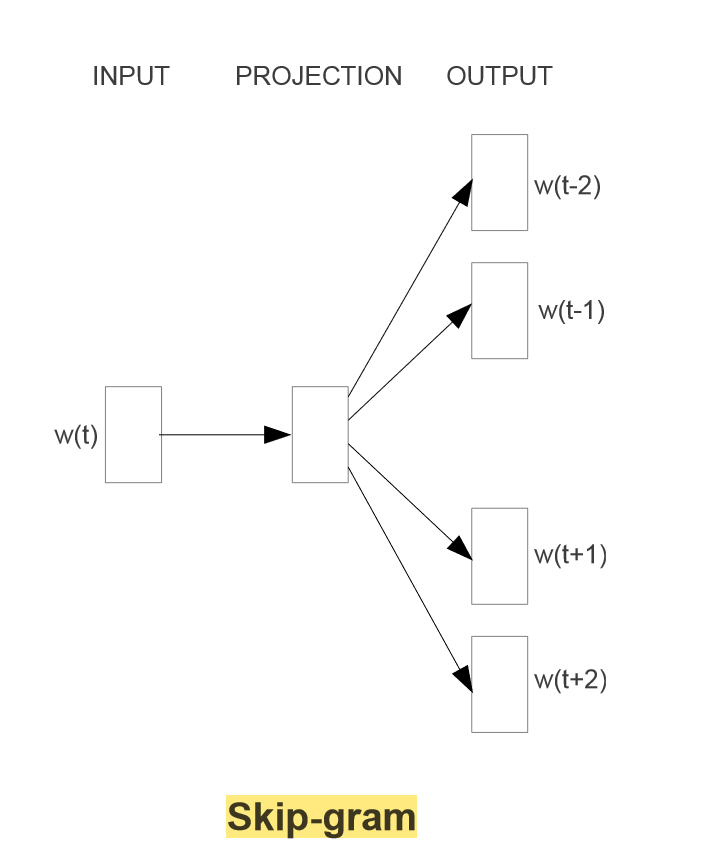
输入层是1xV,隐藏层是1xN,输出层是1xV,那么输入层和隐藏层之间的权重矩阵W是VxN,隐藏层和输出层之间的权重矩阵W’是NxV。实际上,词向量也就是输入层到隐藏层之间的权重矩阵。
在使用softmax的时候,对一个样本的时间复杂度是$O(V)$,V是词汇表的大小,其实是非常大的,可能到几十万或者几百万。为了降低在计算损失函数的复杂度,提出了Hierarchical Softmax,这时候的时间复杂度降到了$O(log(V))$ ,这时候直觉告诉我们,可能是采用了二叉树等结构。
这里注意一点:其实只用二叉树就已经从线性复杂度优化到了对数复杂度,只不过我们这里的二叉树还可以进一步优化,即哈夫曼树,词频高的在上面,词频低的在下面,这样的编码方式会更优化一下路径。
那么我们就以一个简单的例子复习一下哈夫曼树(虽然大家都知道hh)
现在有(a,b,c,d,e,f)6个节点,权重分别是(20,4,8,6,16,3)。建立哈夫曼树如下:

那我们现在正式搞懂一下word2vec的第一种优化方式:Hierarchical Softmax
由于权重高的叶子节点越靠近根节点,而权重低的叶子节点会远离根节点,这样我们的高权重节点编码值较短,而低权重值编码值较长。这保证的树的带权路径最短,也符合我们的信息论,即我们希望越常用的词拥有更短的编码。如何编码呢?一般对于一个霍夫曼树的节点(根节点除外),可以约定左子树编码为0,右子树编码为1.如上图,则可以得到c的编码是00。
在word2vec中,约定编码方式和上面的例子相反,即约定左子树编码为1,右子树编码为0,同时约定左子树的权重不小于右子树的权重。
如下图所示,层次softmax首先利用树结构的叶节点表示词库中的每一个词,从根节点到叶节点的路径,每一个中间路径都对应着一个概率,某个词出现的概率的计算方式改为路径上所有中间路径概率的乘积.
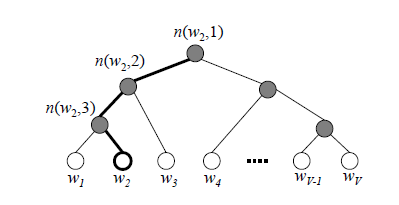
我们要明确,这个二叉树的结构,实际上是对隐藏层到输出层的这部分进行优化的,原因就是这部分用的softmax计算量太大,为了避免要计算所有词的softmax概率,word2vec采样了霍夫曼树来代替从隐藏层到输出softmax层的映射。
那么问题就是我们如何求解每一条路径上每一个分支的概率?这其实是我们最关心的,因为这就是要训练优化的参数。
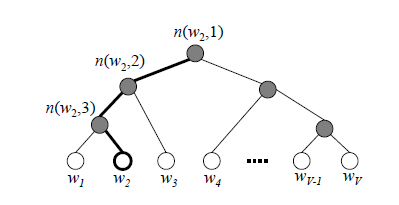
如图,哈夫曼树的每一个节点类比于隐藏层的神经元(之前的softmax就是要到所有的节点,而优化后就只需要对应路径上的),根节点的词向量对应我们隐藏层完成投影后的词向量(也就是输入层与权重矩阵相乘之后的维度),叶子结点类比我们输出层的神经元,叶子结点的个数,也就是词汇表的大小。我们注意,在层次softmax中,我们从隐藏层到输出层这段优化,不是一下子完成,而是沿着一棵树一步步完成的,这也体现出了“层次”的感觉。
那么关键又来到了“如何一步步完成”
我们注意到,由于是二叉树结构,在当前节点决定向下走的时候,只有左孩子和右孩子两种选择,那么就可以用sigmoid函数做一个二分类。
$$P(+)=\sigma(x_w^T\theta)=\frac1{1+e^{-x_w^T\theta}}$$
这里的$x_w^T$是指当前节点的输入向量,$\theta$指的是我们要训练得出的参数(其实我理解的就是一个权重向量,和输入向量点积运算后就能得到一个标量值送入sigmoid函数得出概率)
层次softmax改变了原来模型的结构,原来是一个或多个1V的one-hot向量,经过输入层VD的矩阵(CBOW模式多个输入取平均)变为(1D),再经过隐层(DV)得到(1V)的输出,再经softmax计算出各个词出现的概率;改为层次softmax后,1V的输入,经VD的矩阵得到1D,然后就要改变了,每一个中间路节点(上图中实心球)对应一个向量,该向量的形状为(D,1),然后上面得到的1*D的向量与中间路径向量相乘,得到一个数值z,z输入到sigmod函数得到一个0-1的数值,就是该节点到下一节点向左(或向右)的概率,另外一侧概率是1-sigmod(z),这样就得到了中间路径的概率。
明确了这些,就该理解具体的计算过程了。
还是使用最大似然估计,将每个的概率进行连乘,最大化下面的似然函数(以$w_2$为例):
$$\prod_{i=1}^3P(n(w_i),i)=(1-\frac1{1+e^{-x_w^T\theta_1}})(1-\frac1{1+e^{-x_w^T\theta_2}})\frac1{1+e^{-x_w^T\theta_3}}$$
可以看出,公式还是很简单明了的,就是概率相乘的极大似然估计。
之后为了推公式方便,加了一些的符号表示:
- 输入的词向量为$x_w$
- 从根节点到叶子结点包含的总结点数为$l_w$
- 经过的第i个节点表示为$p_i^w$,对应好的哈夫曼编码为$d_i^w \in {0,1},i=2,3,4,…,l_w$
那么我们就可以得出,在词向量经过哈夫曼树的某一个节点时候,判断其概率值的公式为:
$$\left.P(d_j^w|x_w,\theta_{j-1}^w)=\begin{cases} \sigma(x_w^T\theta_{j-1}^w)&d_j^w=0\\ 1-\sigma(x_w^T\theta_{j-1}^w)&d_j^w=1&\end{cases}\right.$$
有了单个的概率计算,也就有了最大似然,那就是这条路上每个节点的概率乘积:
$$\prod_{j=2}^{l_w}P(d_j^w|x_w,\theta_{j-1}^w)=\prod_{j=2}^{l_w}[\sigma(x_w^T\theta_{j-1}^w)]^{1-d_j^w}[1-\sigma(x_w^T\theta_{j-1}^w)]^{d_j^w}$$
为了便于后面的求导计算,损失函数就可以把最大似然取对数,乘积变加和。
$$L=log\prod_{j=2}^{l_w}P(d_j^w|x_w,\theta_{j-1}^w)=\sum_{j=2}^{l_w}((1-d_j^w)log[\sigma(x_w^T\theta_{j-1}^w)]+d_j^wlog[1-\sigma(x_w^T\theta_{j-1}^w)])$$
之后分别求解对于$x_w$和$权重向量\theta$的梯度进行更新即可,这就按照链式法则即可,过程略hh
$$\begin{aligned} \frac{\partial L}{\partial\theta_{j-1}^w}& =(1-d_j^w)\frac{(\sigma(x_w^T\theta_{j-1}^w)(1-\sigma(x_w^T\theta_{j-1}^w)}{\sigma(x_w^T\theta_{j-1}^w)}x_w-d_j^w\frac{(\sigma(x_w^T\theta_{j-1}^w)(1-\sigma(x_w^T\theta_{j-1}^w)}{1-\sigma(x_w^T\theta_{j-1}^w)}x_w \\ &=(1-d_j^w)(1-\sigma(x_w^T\theta_{j-1}^w))x_w-d_j^w\sigma(x_w^T\theta_{j-1}^w)x_w \\ &=(1-d_j^w-\sigma(x_w^T\theta_{j-1}^w))x_w \end{aligned}$$
$$\frac{\partial L}{\partial x_w}=\sum_{j=2}^{l_w}(1-d_j^w-\sigma(x_w^T\theta_{j-1}^w))\theta_{j-1}^w$$
此刻,我们只是完成了层次softmax算法的普适性理解掌握,但我们都知道,word2vec是有两种看具体的模型架构,即skip-gram和cbow两种。skip更复杂也用的更多,我们先看skip-gram如何应用层次softmax
明确输入
输入只有中心词一个词向量,设置的窗口大小为c,那么输出就是2c个上下文词向量$context$,期望这些词的softmax概率比其他的词大。
明确具体做法
首先将词汇表应建立映射成一棵哈夫曼树。之后用梯度下降法更新两大参数,即词向量(不是输出,是训练过程的附属品)和树结构的参数(即权重向量)。这里我们注意,每次中心词是对应2c个上下文词的,最直观的期望就是最大化$P(x_i|x_w),i=1,2,…,2c$。但中心词和上下文其实是相互对应的,也是相辅相成的,一个词这次是中心词,那么下次就是上下文词了,因此,在期望最大化$P(x_i|x_w),i=1,2,…2c$的同时,也期望最大化$P(x_w|x_i),i=1,2,…,2c$。论文选择的是第二种方法去求取概率,好处很显然:我们使用第一种,就是只固定用到了中心词,去预测2c个,但第二种是每次窗口的迭代,都用到了2c个词,用到的信息更丰富。
突然感慨:这其实是一种我要什么,但不一定非得把它作为输出,作为中间的产物也是一样,只要效果好,word2vec最终的词向量矩阵(输入层到隐藏层的部分)不就是训练skip-gram或CBOW的过程产物嘛?但这俩模型并不那么重要,重要的是获得了非常有用的词向量!这何尝不是一种创新,真牛的思想hhh!
CBOW也是类似,只是输入2c(且真正的输入向量是对这2c个向量加和取平均,做梯度更新完毕后会用梯度项直接更新原始的各个单独的小向量,即加和取平均的那些组成部分)
那么完成的算法过程如下伪代码所示:
# 初始化
initialize_parameters()
initialize_word_vectors()
# 1. 基于语料训练样本建立霍夫曼树
build_huffman_tree()
# 2. 随机初始化所有的模型参数theta,所有的词向量w
for theta in all_theta:
theta = random_initial_value()
for w in all_word_vectors:
w = random_initial_value()
# 3. 进行梯度上升迭代过程
for each training sample (w, context(w)):
# a) For i = 1 to 2c
for i in range(1, 2c+1):
# i) 初始化误差e = 0
e = 0
# ii) For j = 2 to lw
for j in range(2, lw+1):
# 计算 f = sigmoid(xi^T * theta_j^w)
f = sigmoid(dot_product(x_i, theta_j^w))
# 计算 g = (1 - d_j^w - f) * eta
g = (1 - d_j^w - f) * eta
# 累积误差 e = e + g * theta_j^w
e += g * theta_j^w
# 更新模型参数 theta_j^w = theta_j^w + g * x_i
theta_j^w += g * x_i
# iii) 更新词向量 x_i = x_i + e
x_i += e
# b) 检查梯度是否收敛,如果收敛,结束迭代,否则继续迭代
if check_convergence():
break
# Sigmoid函数
def sigmoid(x):
return 1 / (1 + exp(-x))
# 向量点积计算
def dot_product(vec1, vec2):
return sum(v1 * v2 for v1, v2 in zip(vec1, vec2))
# 检查梯度是否收敛
def check_convergence():
# 检查梯度是否收敛的逻辑
pass
# 初始化参数函数
def initialize_parameters():
# 初始化所有的theta和词向量w
pass
# 初始化词向量函数
def initialize_word_vectors():
# 初始化所有的词向量
pass
# 建立霍夫曼树函数
def build_huffman_tree():
# 基于语料训练样本建立霍夫曼树
pass
- 初始化参数和词向量:首先随机初始化模型的所有参数和词向量。
- 建立霍夫曼树:根据训练样本建立霍夫曼树,用于后续编码。
- 梯度上升迭代:
对每个训练样本进行处理。
对于每个样本的上下文,计算误差并更新参数。
计算预测值、误差和梯度,更新模型参数和词向量。
检查梯度是否收敛,如果收敛则结束迭代,否则继续。 - 辅助函数:包括sigmoid函数、向量点积计算、检查收敛等。
至此,我们彻底过完了word2vec中层次化softmax的实现过程(收货满满hh)
但还是不想继续往下走,因为还有一个优化点,就是负采样Negative Sampling,来吧走起!
在一篇博客中看到这样一个观点:
首先要申明一下,这里的负采样和层次softmax是两种独立的优化方法,具体实施时根据问题场景只选用一种方法就可以,基本上没有同时采用这两种方法进行优化的。
这就让我更好奇了哈哈哈,开整!
我们的层次softmax的初衷,就是优化传统softmax计算量太大的问题,这样确实得到了优化,但我们发现大量的经历放在了数据结构上,即哈夫曼树的构造和计算等,其实这也能接受,但如果我们的中心词是一个出现词频极低,比如就在词表中出现了一次,那么毫无疑问就会在最底层的叶子结点上,那这样从根节点到叶子结点沿着分支走下来,每个节点都需要一次点积运算和sigmoid计算,代价也小不了多少。甚至再极端一些,如果中心词频繁出现且都是生僻词,模型每次更新的计算量就会非常大,导致训练过程变慢。,这其实是哈夫曼树本身的缺点,很难去避免和优化了。
因此,负采样就没有再使用哈夫曼树这个数据结构,而是去分析训练样本去了。那么我们具体从负采样如何应用和如何进行采样这两部分来整。
负采样算法过程
我们在语料库建立词表后选取中心词w,此时会有2c个对应的上下文词,我们把这种对应关系叫正例,即(w,context(w))这种词对是相关存在的,那么距离中心词2c之外的所有n个“新中心词”,我们就可以认为这些“新中心词”和当前的上下文词是没有关系的,是不相关的,叫做负例。那么我们就可以根据已有的2c个上下文词,去采样n个和w不同的中心词$w_i,i=1,2,…n$,这样$context(w)$和$w_i$组成了n个负例。这也就是所谓的“1个正例,n个负例”。
到了算法正式开始的时候。我们将正例记为$w_0$,负例记为$w_i,i=1,2,…,n$。我们的正例期望最大化概率:
$$P(context(w_0),w_i)=\sigma(x_{w_0}^T\theta^{w_i}),y_i=1,i=0$$
我们的负例期望最大化概率:
$$P(context(w_0),w_i)=1-\sigma(x_{w_0}^T\theta^{w_i}),y_i=0,i=1,2,\ldots neg$$
那正负例合起来,我们期望最大化概率:
$$\prod_{i=0}^{neg}P(context(w_0),w_i)=\sigma(x_{w_0}^T\theta^{w_0})\prod_{i=1}^{neg}(1-\sigma(x_{w_0}^T\theta^{w_i}))$$
那很容易写出了我们的最大似然函数,就是n个概率的乘积:
$$\prod_{i=0}^{neg}\sigma(x_{w_0}^T\theta^{w_i})^{y_i}(1-\sigma(x_{w_0}^T\theta^{w_i}))^{1-y_i}$$
为了求梯度的时候好求解,还是传统的技巧,两边去对数,将乘积变为加和。
$$L=\sum_{i=0}^{neg}y_ilog(\sigma(x_{w_0}^T\theta^{w_i}))+(1-y_i)log(1-\sigma(x_{w_0}^T\theta^{w_i}))$$
需要更新的参数主要就是两大类,一个是词向量$x_w$,一个是负例的向量,分别求梯度即可。
词向量梯度:
$$\frac{\partial L}{\partial x^{w_0}}=\sum_{i=0}^{neg}(y_i-\sigma(x_{w_0}^T\theta^{w_i}))\theta^{w_i}$$
负例向量梯度:
$$\begin{aligned} \frac{\partial L}{\partial\theta^{w_i}}& =y_i(1-\sigma(x_{w_0}^T\theta^{w_i}))x_{w_0}-(1-y_i)\sigma(x_{w_0}^T\theta^{w_i})x_{w_0} \\ &=(y_i-\sigma(x_{w_0}^T\theta^{w_i}))x_{w_0} \end{aligned}$$
这样就可以用梯度下降/上升来迭代优化了。
如何采样
- 将长度为1的线段平均分成V份,V是词汇表的大小。其实这个操作本身意义只是在于让每个单词初始所占比重完全相同。
- 根据每个词在词汇表中出现词频的不同,进行计算每个词占的长度:
$$len(w)=\frac{count(w)^{3/4}}{\sum_{u\in vocab}count(u)^{3/4}}$$ - 词频乘以平均分的V份,得到每一份占得权重。
- 再将长度为1的线段平均分成M份,M>>V,一般选择为$10^8$,目的是这种细化使得每个小段的长度非常短,从而使得采样的粒度非常细,可以更准确地反映每个词的采样概率。
- 那么就从这M个位置中随机选择n个位置作为负例,这种方法减少了采样的计算复杂度,因为只需在一个预先划分好的大数组中进行随机选择,而无需每次都进行复杂的概率计算。
如图:
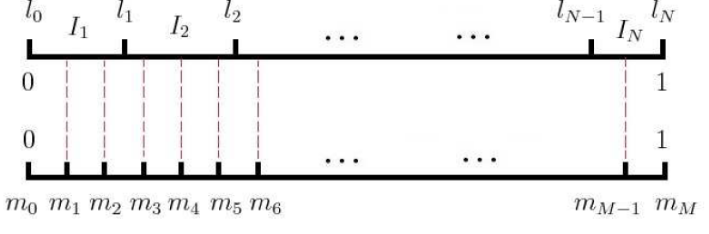
以一个具体的小例子展开说,就很形象啦~
假设词汇表中有4个词:$w_1,w_2,w_3,w_4$
1. 分成V份(也就是4份)
- 根据词频,计算得出$len(w_1)=0.4$,$len(w_2)=0.3$,$len(w_3)=0.2$,$len(w_4)=0.1$
- 这意味着在长度为1的线段中,$w_1$占0.4,$w_2$占0.3,以此类推。
2. 分成M份(M=10^8)
- 总长度为1的分成M份,每一份为$10^{-8}$
- 根据之前分配的长度,$w_1$对应包含$0.4 \times 10^{-8}=4 \times 10^{-7}$,以此类推
3. 随机采样
- 在$10^{-8}$份中随机选择n个位置作为负样本
伪代码:
# 初始化词频和采样概率
vocab = {...} # 词汇表
count = {...} # 词频表
M = 10**8 # 采样分割数量
neg = ... # 负样本数量
# 计算采样概率 len(w)
len_w = {w: (count[w]**(3/4)) / sum(count[u]**(3/4) for u in vocab) for w in vocab}
# 构建采样区间
sampling_interval = []
for w, length in len_w.items():
sampling_interval.extend([w] * int(length * M))
# 进行负采样
negative_samples = random.sample(sampling_interval, neg)
# 输出负样本
print(negative_samples)
负采样的比例一般控制到1:10,也就是窗口最多是$2c+1$个词,那么最多采样$2k \times c$个负样本。所以求解梯度的时候,矩阵是很稀疏的,很多位置是0.
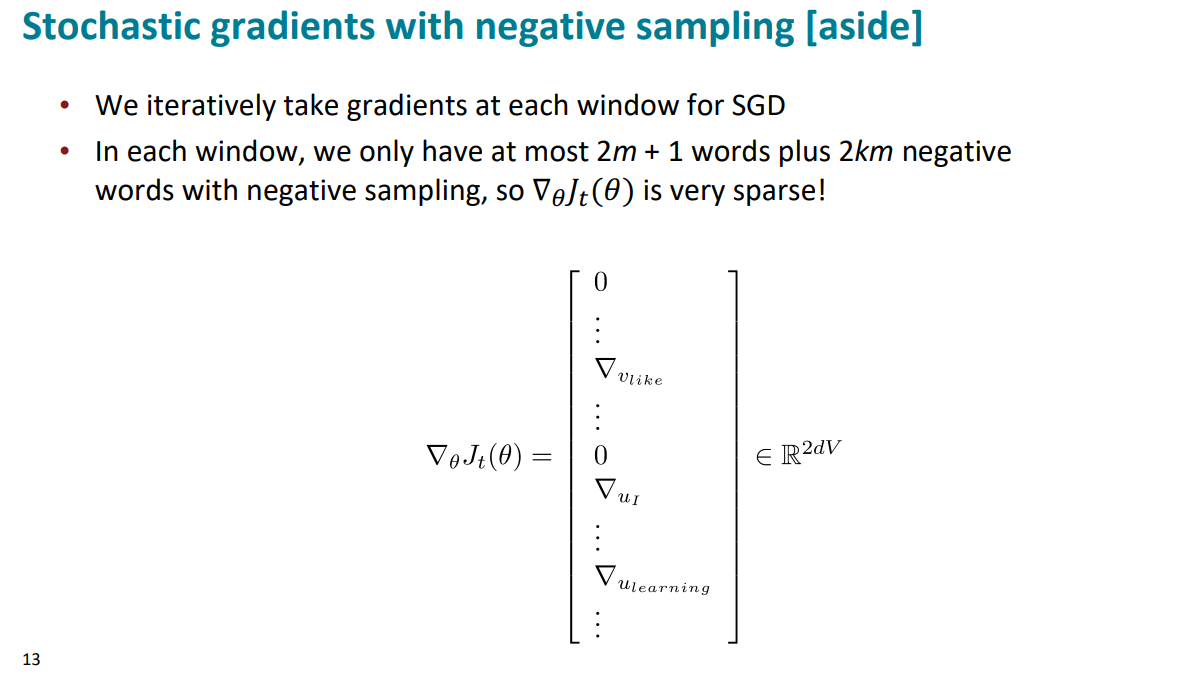
因此负采样技术出现了新问题:随机梯度下降的时候,仅更新实际出现的词向量,但现在的计算方式会更新全部的词向量,带来很大的开销。
解决方法:
- 利用稀疏矩阵更新操作,只更新全词向量矩阵中的某些行,而不是整个矩阵。如pytorch中的实现
embedding = torch.nn.Embedding(num_embeddings, embedding_dim, sparse=True) - 利用哈希表存储词向量而不是矩阵。
word_vectors = {}
for word in vocabulary:
word_vectors[word] = np.random.rand(embedding_dim)
# 更新实际出现的词向量
for word in words_in_batch:
word_vectors[word] += gradient_update

到此为止,我们就搞通了一遍word2vec中两大优化措施,感觉我是彻底明白了hhh
1. 层次softmax
2. 负采样技术(skip-gram版本的叫sgns)
这确实是两种独立的优化措施,有点儿理解为啥有博主说基本不会同时使用。负采样有点儿觉得层次softmax在某种情况(上面提到了)可能计算效率优化还不够好,做出的一种新的举措,如果同时使用这两种,确实有些矛盾感觉hhh
至此,word2vec就这样吧,应该比较细致啦~
参考
https://www.cnblogs.com/pinard/p/7249903.html
https://www.cnblogs.com/pinard/p/7243513.html
https://zhuanlan.zhihu.com/p/568064512
[1] Mikolov T, Chen K, Corrado G, et al. Efficient Estimation of Word Representations in Vector Space[A]. arXiv, 2013.

