DAG 上的动态规划
$\color{blue}{有向无环图模型}$
矩形嵌套
有 $n$ 个矩形,每个矩形可以用 $a,b$ 来描述,表示长和宽。矩形 $X (a,b)$ 可以嵌套在矩形 $Y(c,d)$ 中当且仅当 $a<c,b<d$ 或者 $b<c,a<d$(相当于旋转$X90$ 度)。例如 $(1, 5)$ 可以嵌套在 $(6,2)$ 内,但不能嵌套在 $(3, 4)$ 中。你的任务是选出尽可能多的矩形排成一行,使得除最后一个外,每一个矩形都可以嵌套在下一个矩形内。
分析:
- 矩形之间的 “可嵌套” 关系是个有方向的二元关系,可以用有向图来建模。如果 $X$ 能嵌套在 $Y$ 内部,则从 $X$ 到 $Y$ 连一条边。这个有向图是无环的,因为一个矩形无法直接或间接嵌套在自己内部。则本题转化为求图上的最长路径。
- $dp[i]$ 表示 $i$ 开头的最长路径的长度
- $dp[i] = max(dp[j] + 1), (i,j) \in E$
- 最后统计 $dp[i]$ 中最大的即可
int f(int x) {
if (dp[x] > 0) {
return dp[x];
}
dp[x] = 1;
for (int i = 0; i < n; ++i) {
if (adj[x][i]) {
dp[x] = max(dp[x], f(i) + 1);
}
}
return dp[x];
}
地铁间谍
特工玛利亚被送到 $S$ 市执行一个特别危险的任务。她需要利用地铁完成他的任务,$S$ 市的地铁只有一条线路运行,所以并不复杂。
玛利亚有一个任务,现在的时间为 $0$,她要从第一个站出发,并在最后一站的间谍碰头。玛利亚知道有一个强大的组织正在追踪她,她知道如果一直呆在一个车站,她会有很大的被抓的风险,躲在运行的列车中是比较安全的。所以,她决定尽可能地呆在运行的列车中,她只能往前或往后坐车。
玛利亚为了能准时且安全的到达最后一个车站与对方碰头,需要知道在在车站最小等待时间总和的计划。你必须写一个程序,得到玛丽亚最短的等待时间。当然,到了终点站之后如果时间还没有到规定的时刻,她可以在车站里等着对方,只不过这个等待的时刻也是要算进去的。
这个城市有 $n$ 个车站,编号是 $1-n$,火车是这么移动的:从第一个车站开到最后一个车站。或者从最后一站发车然后开会来。火车在每特定两站之间行驶的时间是固定的,我们也可以忽略停车的时间,玛利亚的速度极快,所以他可以迅速上下车即使两辆车同时到站。
时间是单向流逝的,以时间为单位划分阶段。影响决策的是当前时间和所处车站
#include <bits/stdc++.h>
using std::cin;
using std::cout;
using std::min;
using std::memset;
const int INF = 5000;
int n, t, kase, m1, m2;
int ti[55]; // ti[i]表示i站到i+1站之间的时间
int hasTrain[2005][55][2]; // hasTrain[i][j][0]表示第i时刻,在车站j,是否有车向右开,hasTrain[i][j][1]表示向右开
int dp[2005][55]; // dp[i][j]表示在第i时刻,在车站j,最少等待时间
int main() {
cin >> n;
while (n) {
cin >> t;
kase++;
memset(hasTrain, 0, sizeof hasTrain);
for (int i = 1; i <= n - 1; ++i) cin >> ti[i];
cin >> m1;
for (int i = 0; i < m1; ++i) {
int d; cin >> d;
for (int j = 1; j <= n; ++j) {
if (d <= t) {
hasTrain[d][j][0] = 1;
d += ti[j];
}
}
}
cin >> m2;
for (int i = 0; i < m2; ++i) {
int e; cin >> e;
for (int j = n; j >= 1; --j) {
if (e <= t) {
hasTrain[e][j][1] = 1;
e += ti[j - 1];
}
}
}
// 时间到了,站在非终点站都不行
for (int j = 0; j < n; ++j) {
dp[t][j] = INF;
}
// 最后时刻,站在终点站,无需等待
dp[t][n] = 0;
for (int i = t - 1; i >= 0; --i) {
for (int j = 1; j <= n; ++j) {
// 第一种决策是站着不动
dp[i][j] = dp[i + 1][j] + 1;
// 第二种决策是往右走
if (j < n and i + ti[j] <= t and hasTrain[i][j][0]) {
dp[i][j] = min(dp[i][j], dp[i + ti[j]][j + 1]);
}
// 第三种决策是往左走
if (j > 1 and i + ti[j - 1] <= t and hasTrain[i][j][1]) {
dp[i][j] = min(dp[i][j], dp[i + ti[j - 1]][j - 1]);
}
}
}
if (dp[0][1] >= INF) {
cout << "Case Number " << kase << ": impossible" << '\n';
}
else {
cout << "Case Number " << kase << ":" << dp[0][1] << '\n';
}
cin >> n;
}
return 0;
}
树形dp
树是一种 $n$ 个点 $n − 1$ 条边组成的无向联通图。
树形 $\rm DP$ 指的是在树上进行一些有关树节点或者边的一些动态规划。和其他动态规划不同,树形 $\rm DP$ 的难度从最简单到最难都有分布,这里只给大家讲几个基本的模型。
没有上司的舞会
某大学有 $n$ 个职员,编号为 $1\ldots n$。
他们之间有从属关系,也就是说他们的关系就像一棵以校长为根的树,父结点就是子结点的直接上司。
现在有个周年庆宴会,宴会每邀请来一个职员都会增加一定的快乐指数 $r_i$,但是呢,如果某个职员的直接上司来参加舞会了,那么这个职员就无论如何也不肯来参加舞会了。
所以,请你编程计算,邀请哪些职员可以使快乐指数最大,求最大的快乐指数。
分析:
- 对于每个点 $u$,$dp[u][0]$ 表示它为根的子树,$u$ 不参加舞会的时候的最大快乐指数
$dp[u][1]$ 表示 $u$ 参加时候的最大快乐指数 - 如果 $u$ 不参加,设 $v$ 为它所有子节点,则所有子节点可以选择参加或者不参加。
- 如果 $u$ 参加,则所有子节点都不能参加。
void f(int root) {
dp[root][0] = 0;
dp[root][1] = r[root];
for (int i = 0; i < employee[root].size(); ++i) {
int v = employee[root][i];
f(v);
dp[root][0] += max(dp[v][0], dp[v][1]);
dp[root][1] += dp[v][0];
}
}
二叉苹果树
有一棵苹果树,如果树枝有分叉,一定是分2叉(就是说没有只有 $1$ 个儿子的结点)
这棵树共有 $N$ 个结点(叶子点或者树枝分叉点),编号为 $1-N$,树根编号一定是1。
我们用一根树枝两端连接的结点的编号来描述一根树枝的位置。下面是一颗有 $4$ 个树枝的树

现在这颗树枝条太多了,需要剪枝。但是一些树枝上长有苹果。
给定需要保留的树枝数量,求出最多能留住多少苹果。
输入格式
第 $1$ 行 $2$ 个数,$N$ 和 $Q$($1<=Q<= N,1<N<=100$)。
N表示树的结点数,$Q$ 表示要保留的树枝数量。接下来 $N-1$ 行描述树枝的信息。
每行 $3$ 个整数,前两个是它连接的结点的编号。第 $3$ 个数是这根树枝上苹果的数量。
每根树枝上的苹果不超过 $30000$ 个。
输出格式
一个数,最多能留住的苹果的数量。
分析:
int dp[MAXN][MAXN]; // dp[i][j] 表示以 i 为根的子树,保留 j 条边,最大苹果数
对于任何以 $u$ 为根的子树,可以选:
1. 两个孩子都不要
2. 只要左孩子
3. 只要右孩子
4. 两个孩子都要
void dfs(int u, int father) {
dp[u][0] = 0;
if (adj[u].size() == 1) return; // 叶子节点
for (int i = 0; i < adj[u].size(); ++i) {
if (adj[u][i].to == father) {
adj[u].erase(adj[u].begin() + i);
break;
}
}
Edge left = adj[u][0];
Edge right = adj[u][1];
dfs(left.to, u); dfs(right.to, u);
dp[u][1] = max(left.apple, right.apple);
for (int i = 2; i <= q; ++i) {
// 只要左儿子
dp[u][i] = max(dp[u][i], dp[left.to][i - 1] + left.apple);
// 只要右儿子
dp[u][i] = max(dp[u][i], dp[right.to][i - 1] + right.apple);
// 左右都要
for (int j = 0; j <= i - 2; ++j) {
dp[u][i] = max(dp[u][i], dp[left.to][j] + dp[right.to][i - 2 - j] + left.apple + right.apple);
}
}
}
树的重心
树的重心的定义:
树若以某点为根,使得该树最大子树的节点数最小,那么这个点则为该树的重心,一棵树可能有多个重心。换句话说,删除这个点以后,最大连通块的节点数最小,这个点是该树的重心。
树的重心的性质:
- 树上所有的点到树的重心的距离之和是最短的,如果有多个重心,那么总距离相等。
- 插入或删除一个点,树的重心的位置最多移动一个单位。
- 若添加一条边连接 $2$ 颗树,那么新树的重心一定在原来两颗树的重心的路径上。
例题:医院设置
设有一棵二叉树,如图:
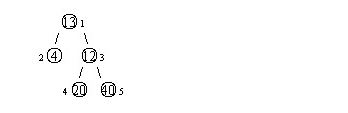
其中,圈中的数字表示结点中居民的人口。圈边上数字表示结点编号,现在要求在某个结点上建立一个医院,使所有居民所走的路程之和为最小,同时约定,相邻接点之间的距离为 $1$。如上图中,若医院建在 $1$ 处,则距离和 $=4+12+2\times20+2\times40=136$;若医院建在 $3$ 处,则距离和 $=4\times2+13+20+40=81$。
分析:
设四个数组:
int depth[MAXN]; // 每个点的深度,1的深度是0
int size[MAXN]; // 以 i 点为根的子树包含的人数
int dp[MAXN]; // i 点到其他点的加权距离
int w[MAXN]; // 每个点的权
先以 $1$ 为根,遍历一遍整个树,计算出 $depth, size$ 数组,还可以计算出 $dp[1]$
$$
dp[1] = \sum_{i = 2}^n w[i] * depth[i]
$$
然后再遍历一次,从父节点 $u$,推子节点 $v$ 的 $dp$ 值
$$
dp[v] = dp[u] - size[v] + size[1] - size[v]
$$
即 $v$ 点的值,对于 $v$ 这颗子树里面所有的点,都相对于 $dp[u]$ 少了 $size[v]$,但是其他点距离多了 $1$。其他点的个数是 $size[1] - size[v]$。
void dfs(int v, int p = -1) {
dep[v] = dep[p] + 1;
size[u] = w[u];
f[1] += w[u] * dep[u];
for (int u : to[u]) {
if (u == p) continue;
dfs(v, u);
size[u] += size[v];
}
}
void reroot(int v, int p = -1) {
for (int u : to[v]) {
if (u == p) continue;
f[u] = f[v] + size[1] - 2 * size[u];
reroot(u, v);
}
ans = min(ans, f[v]);
}
求树的直径
树的直径是数中最长的一条链。给定一颗树,求树的直径长度。一种比较常见的做法是两遍搜索,连续着两次最长链,但是这种做法不支持负权,考虑有没有什么更优秀的做法。
我们不妨枚举直径在树上转弯的点。所以我们维护出到一个节点时向下的最长链和次长链,然后用二者相加和来更新答案,同时更新父亲节点的最长链和次长链。
Code:
void dfs(int v, int p = -1) {
for (auto e : g[v]) {
if (e.to == p) continue;
int u = e.to, w = e.co;
dfs(u, v);
if (dp[0][u] + w > dp[0][v]) { // dp[0]:最长链,dp[1]:次长链
dp[1][v] = dp[0][v];
dp[0][v] = dp[0][u] + w;
}
else if (dp[0][u] + w > dp[1][v]) {
dp[1][v] = dp[0][u] + w;
}
}
ans = max(ans, dp[0][v] + dp[1][v]);
}

