整数二分模板

二分算法

思路：

假设目标在闭区间[l,r]中，每一次将区间长度缩小一半，当l==r即区间长度为1时，答案就找到了。

人话

给定一个闭区间，在边界上定义某种性质，把该区间一分为二，一半满足该性质，一半不满足，那么继续对满足条件的区间进行二分。这样下去，就可以找到其边界。

二分的两个模板

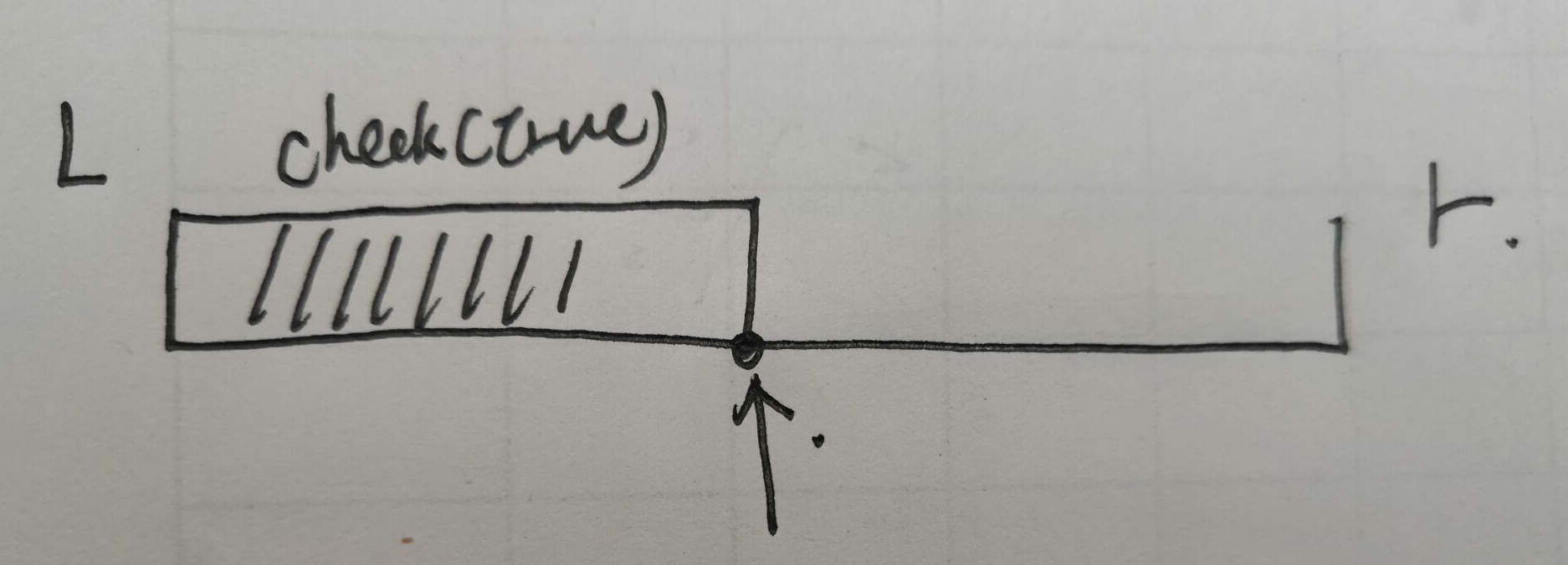
找到右边界

具体代码实现

int bsearch1(int l,int r){
    while(l<r){
        int mid=l+r+1>>1;
    if(check(mid)){
        l=mid;
    }else{
        r=mid-1;}
    }
    return l;
}

代码解释：

图中阴影部分为check()函数为真的区间，

如果mid满足条件，那么答案在[mid,r]中，所以区间更新为l=mid;

反之，答案就在[l,mid-1]中,区间更新为r=mid-1;

这样的话，原来的区间就被划分成了[l,mid-1]和[mid,r]。（模板的区间划分）

这里mid =l+r+1>>1;

原因在于，当 l=r-1 时，如果不加1， 那么mid=l ;

如果此时的check(mid)返回值为true，那么新的区间仍然是[l,r];会造成死循环。

找右边界加一

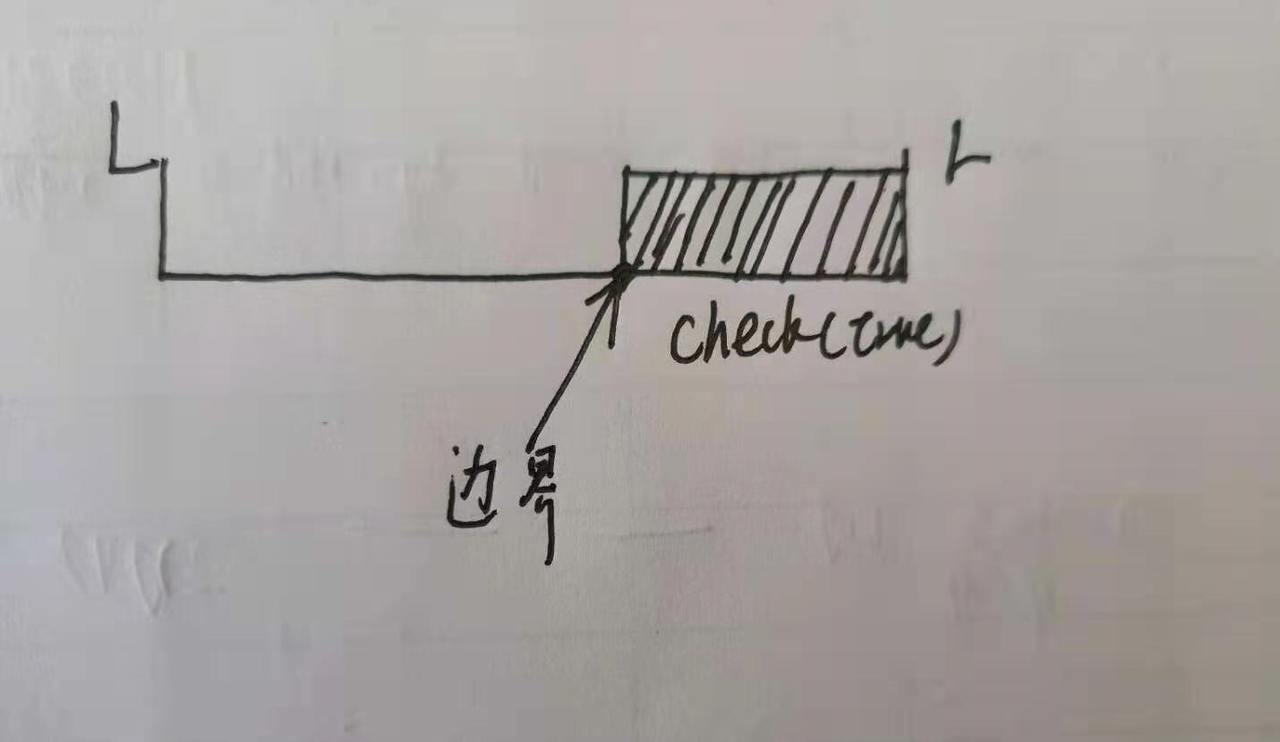
找到左边界

具体代码实现

int bsearch2(int l,int r){
    while(l<r){
        int mid =l+r>>1;
    if(check(mid)){
        r=mid;
    }else{
        l=mid+1;
    }
    }
    return l;
}

代码解释：

图中阴影部分为check()函数为真的区间，

如果mid满足条件，那么答案在[l,mid]中，所以区间更新为r=mid;

反之，答案就在[mid+1,r]中,区间更新为l=mid+1;

这样的话，原来的区间就被划分成了[l,mid]和[mid+1,r]。（模板的区间划分）

注意事项：

1. 二分是一定可以找到边界的，如果找不到，那么就是题目设置的没有。比如说：要找一段数字里面的>=x的第一个数，如果这个数不存在，那么找到的就是第一个大于这个数的位置。
2. 二分不一定与单调性有关，找一个能把区间分为满足和不满足的性质即可，也就是说有单调性一定可以二分，但是能二分，不一定具有单调性。

模板的具体用法

先在不考虑加一的情况下写出mid;

在根据check函数，划分区间，根据区间划分的结果，

再考虑mid= (l+r+1)/2 是否需要加1。