原文的$\text{PDF}$所在网址：点击此处跳转

前置：关于$\text{SpMV}$算法

（该部分此后会分离成单独的帖子，详细介绍该算法）
$\text{SpMV}$为$\text{Sparse Matrix Vector multiplication}$的缩写，即稀疏矩阵向量乘$y=Ax$（用矩阵$A$乘向量$x$得到向量$y$）。对它的研究大多数来源于科学、工程问题中的数值计算，比如微分方程的离散化求解方法，以及稀疏线性系统的迭代求解方法（其中$\text{SpMV}$占总计算量的$60\%\sim 70\%$），随后扩充到了图算法、机器学习等多个领域。受益于矩阵乘法运算的高度可并行性，以及面向图形处理器($\text{GPU}$)的$\text{CUDA}$编程模型的推出，21世纪以来对该算法的优化研究主要针对$\text{GPU}$平台。
稀疏矩阵指的是非零元素占比较大（$90\%甚至99.99\%$）的矩阵，用一般的二维数组存储必然会浪费大量计算资源和存储空间，因此稀疏矩阵有其特别的存储方式。自$\text{COO,CSR,ELL}$等稀疏矩阵存储格式被应用在$\text{GPU}$上之后，研究确实取得了一定的进展，但随着矩阵规模日益增大，以及非零元分布多样化，人们逐渐发现了$\text{SpMV}$并行计算时各线程的负载不均衡现象，以及各存储格式对于$\text{SpMV}$算法来说并不存在“绝对的最优性”一说。因此，围绕“最小化零填充”“负载均衡”和“自适应优化方法”这三个主题及其结合的研究就此展开。

论文总体介绍

$\text{SpMV}$算法优化面临的主要问题：
1. 存储器带宽利用不充分，某些基本格式没有考虑矩阵的空间结构，因此导致了乘向量的重用性较差；
2. 矩阵的微观结构尚未被重视，即便是自适应方法中最先进的人工智能方法，也只考虑了矩阵整体的结构，很少有某项研究能够洞察到矩阵的微观结构

本文涉及的主要工作如下：
1. 提出了针对矩阵微观结构进行的优化方法$\text{TileSpMV}$，将较大的稀疏矩阵划分为若干较小的二维稀疏块$\text{(tile)}$，并为每个小块分别选择最佳格式（每一个小块的规模小到可以用$\text{CUDA}$的单个$\text{warp}$完成计算）；
2. 采用了分级存储的方式，分别存储了原矩阵分块的信息，以及各块内部的信息，并使内核在并行计算时，将每一个小块视作调度的单位，而非原生的行或列；
3. 针对分块后每个小块内部的元素分布特征，设计了一种自适应的选择方法，对应了7种不同的存储格式及算法
4. 验证了自适应方法及分离部分稀疏块的策略相较于单一选择策略的有效性，以及与多种单一格式相比均获得较大的计算效率提升

主要方法详解

7种格式

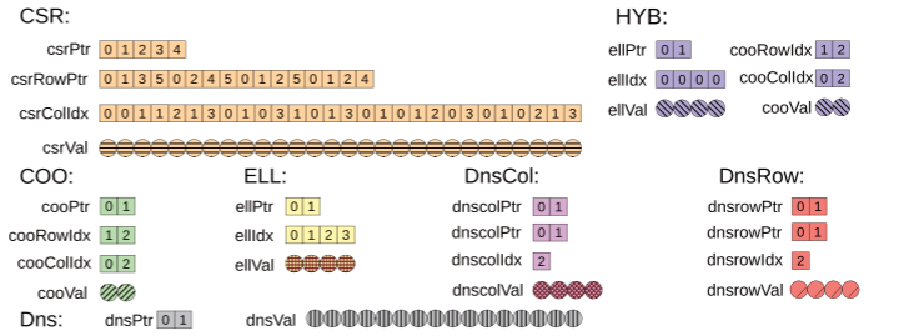
1. 密集存储($\text{Dense}$)：即一般的二维数组，面对块内零元素较多的情况时，效率会大大降低，比较适用于块内非零元占比较大的块；
2. 坐标存储($\text{COO}$)：用三元组$(row, col, val)$即（行，列，值）存储每一个非零元，由于行与列的位置信息也需要额外空间存储，且失去了访问元素的局部性，该格式比较适用于非零元占比很小的块；
   
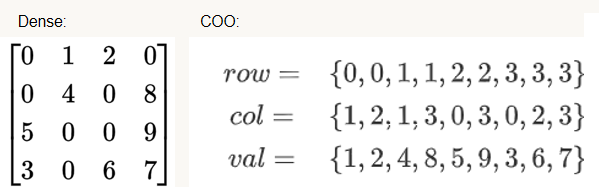
3. 压缩稀疏行($\text{CSR}$)：列、值信息用类似于$\text{COO}$的方式存储（数组$colIdx,values$），同时确保同一行的元素存储连续，另外用数组$rowOfs$（行偏移值）定位出每一行的元素所处的位置；
4. $\text{ELLPack(ELL)}$：省去了$\text{CSR}$的$rowOfs$数组，将$colIdx,values$转化为二维数组，每一行与原矩阵的每一行对应，并增加了空元素填充以占位（一般$colIdx$填充-1，$values$填充0）；
   
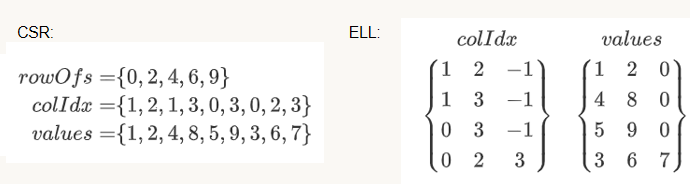
5. 混合存储($\text{HYB}$)：即$\text{ELL}$与$\text{COO}$的结合
   
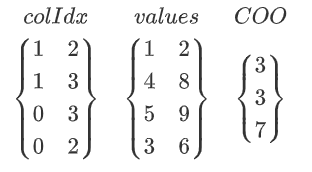
   6,7. 密集行/列($DnsRow,DnsCol$)：只完整存储含有非零元的部分行与列
   

两级存储结构

$\text{TileSpMV}$对矩阵的存储共分为两级：
第一级是对原矩阵的划分情况。按照固定的大小将原矩阵分块后，不一定每一块内都能含有非零元，此时划分完成的所有小块构成一个稀疏矩阵，其中的元素可以为块内包含的非零元数量$nnz$。对它的存储可以用类似于$\text{CSR}$的方式，但是$nnz$的数组是用前缀累加的方式，和$\text{CSR}$的$rowOfs$一样

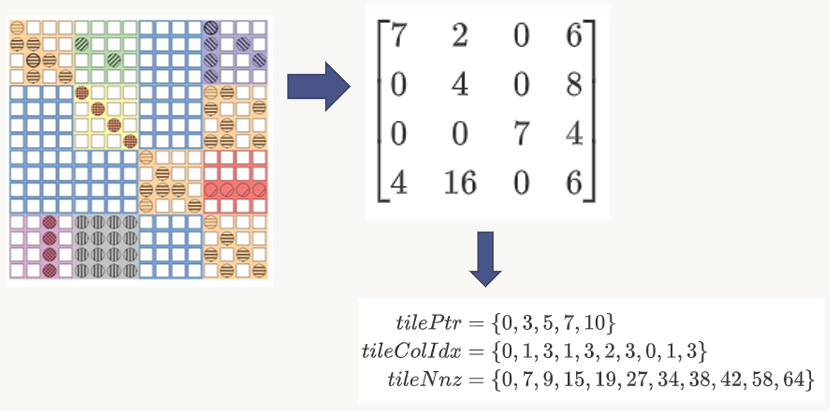
第二级是每一块内部的非零元信息。从图块到相应存储格式，还需要经过自适应方法的选择，上图中的是选择后的结果，由于可能有多块选择了同一种格式，存储时要为每一种格式增加一个数组$ofs$，用来表征当前计算到的是该种格式的第几块

本文中示例图中块大小全为$4*4$，而实际的实验以及后续的伪代码中，块大小为$16*16$

存储方面的差异

1. $\text{CSR}$格式：由于$rowOfs$末尾元素必然为块内的非零元总数，而它可以由第一级存储获取，因此去掉了末尾元素。剩余16个元素用8位的$uchar$类型来存储，因为这些元素的值必然不会超过240；
2. $\text{COO}$格式：每一个三元组$(row,col,val)$中，考虑到$16*16$的块大小，可以用一个8位$uchar$类型的高4位和低4位分别表示$row, col$；
3. 除$\text{COO}$格式外所有涉及下标的数组，全都将相邻的两个值存入同一个$uchar$
   
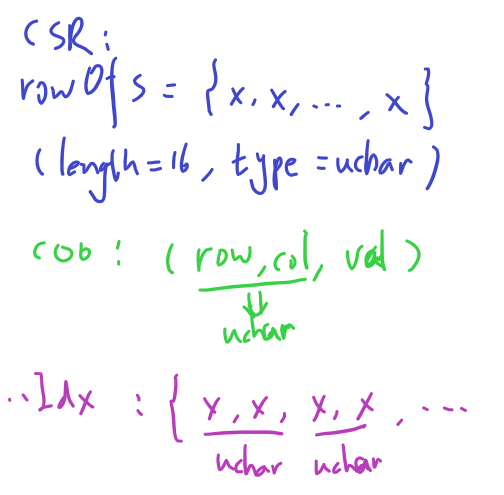
   （下篇在此）