第四讲 数学知识
前言
水平不够,随便写写。如有错误,敬请原谅。仅讲结论,不讲证明。
质数
试除法判断质数
如果要判断$N$是否是质数,传统的方法是枚举 $1 < x < N$ ,来证明这个范围内都满足$x\nmid N$,但时间复N杂度是$O(N)$,遇到大数据则非常麻烦。
但是我们知道,如果 $x \mid N$ ,那么 $\frac{N}{x} \mid N$ ,也就是说,若枚举过 $x$ ,就无需再枚举 $\frac{N}{x}$ ,由此,我们无需枚举$1 < x < N$,只需要枚举 $[2, \sqrt{N}]$ 即可,时间复杂度降到 $O(\sqrt{N})$ 。
代码
bool isPrime(int n){
for (int i = 2; i <= n / i; i ++ )
if (n % i == 0) return 0;
return 1;
}
分解质因数
如果要将$N$分解为质因数的乘积,即如下的公式:
$$
N = \prod p_i^{c_i}
$$
其中$p_i$表示质数,$c_i$表示质因子$p_i$的次数,那么可以从小到大枚举质数,若找到质数,那么要将$N$整除这个质数直至无法整除,而整除的次数即为这个质数的次数。
代码
typedef pair<int, int> pii;
vector<pii> getPrimes(int n){
vector<pii> res;
for (int i = 2; i <= n / i; i ++ ){
int a = 0;
while (n % i == 0)
n /= i, a ++ ;
if (a) res.push_back({i, a});
}
if (n > 1) res.push_back({n, 1});
return res;
}
筛质数
给一整数$N$,需要你求出$[1, N]$中有多少个质数。
最朴素的做法是,在该区间枚举每个数是否是质数,也就是每个数都要经过isPrime()的函数来判断质数,但是复杂度为$O(N\sqrt{N})$。
现在介绍比较优的算法:埃氏筛法。
如果我们知道一个数为质数,那么任何一个大于$1$的数乘上这个质数所得到的数都不可能为质数,因此我们可以在区间$[2,N]$中从小到大枚举,如果遇到质数,则将所有这个质数的倍数 $pk,k\in Z$ 筛去即可,时间复杂度为$O(Nlog^2N)$。
代码
bool vis[N];
int getPrimesNum(int n){
int res = 0;
for (int i = 2; i <= n; i ++ )
if (!vis[i]){
res ++ ;
for (int j = 2; j <= n / i; j ++ )
vis[i * j] = 1;
}
return res;
}
有一种更优的指数筛法:欧拉筛法(线性筛法)。
如果使用埃氏筛法,则会出现一些数字被多次筛去,浪费了时间;而如果用线性筛法,就会大大避免这种情况的发生。
在 $[2,N]$ 中从小到大枚举时,都进行质数筛,不同的是每次都会将枚举到的数乘上已知的质数来筛,如果 $p_j \mid i$ 则可以停下,因为这样已经说明 $i$ 已经被筛过了。时间复杂度为 $O(N)$。
代码
int primes[N];
bool vis[N];
int getPrimesNum(int n){
int res = 0, cnt = 0;
for (int i = 2; i <= n; i ++ ){
if (!vis[i])
primes[res ++ ] = i;
for (int j = 0; primes[j] <= n / i; j ++ ){
vis[primes[j] * i] = 1;
if (i % primes[j] == 0) break;
}
}
return res;
}
约数
试除法求约数
如果我们要求出 $N$ 的所有约数,最朴素的做法是直接枚举。我们已经学了试除法,那么可以借用试除法的思想来获取约数,这里对试除法不再赘述。时间复杂度同样为$O(\sqrt{N})$。
代码
vector<int> getDivisors(int n){
vector<int> res;
for (int i = 1; i <= n / i; i ++ )
if (n % i == 0){
res.push_back(i);
if (i != n / i)
res.push_back(n / i);
}
sort(res.begin(), res.end());
return res;
}
约数个数
给定一个 $n$ 个正整数 $a_i$,求出这些数的乘积的约数个数。
我们朴素的做法是,先将这 $n$ 个数乘起来,再用getDivisors()求出所有因数来获得约数个数,但这种方法在这 $n$ 个数的乘积很大的时候就做不了(会溢出)。
比较优的方法是:分别用getPrimes()求出这 $n$ 个数的质因数的个数和次数,这时候:
$$
a_i = \prod p_j ^ {c_j}
$$
从这可以获得 $a_i$的质因数和次数,这样获得其他数的质因数和次数之后,我们可以用组合的知识来获得每个因数的个数,所以这 $n$ 个数的乘积最终可以化为:
$$
\prod a_i = \prod p_j ^ {c_j}
$$
对于每个 $p_j$ 都有 $c_j$ 个,可以枚举:$1, p_j,p_j ^ 2…p_j^{c_j}$,共 $c_j + 1$ 种因子。
最后用组合数学来求出因子的个数:
$$
ans = \prod (c_j + 1)
$$
代码
int getDivisorsNum(vector<int> muls){
long long res = 1;
unordered_map<int, int> primes;
for (auto it : muls){
auto a = getPrimes(it);
for (auto it2 : a)
primes[it2.first] += it2.second;
}
for (auto it : primes) res = res * (it.second + 1) % Mod;
return res;
}
约数之和
原理和约数个数基本相同,用getPrimes()来求出所有质因子和次数,对于每个 $p_j$ 有$c_j$ ,可以枚举共 $c_j + 1$ 种因子:$1, p_j, p_j ^ 2 …p_j ^ {c_j}$,对其求和用秦九韶算法即可(这个公式看不懂可以直接看getDivisorsSum()代码中的 $t$ 怎么算的):
$$
s_i = 1 + p_j + p_j ^ 2 +… = 1 + p_j(1 + p_j(1 + …p_j(1 + p_j·1)…))
$$
最后求出 $s_i$ 的乘积:
$$
ans = \prod s_i
$$
代码
int getDivisorsSum(vector<int> divisors){
int ans = 1;
unordered_map<int, int> primes;
for (auto it : divisors){
auto vec = getPrimes(it);
for (auto it2 : vec)
primes[it2.first] += it2.second;
}
for (auto it : primes){
int a = it.first, b = it.second;
long long t = 1;
while (b -- ) t = (t * a + 1) % Mod;
ans = ans * t % Mod;
}
return ans;
}
最大公因数
本质是辗转相除法:(a,b是被求的数)
$$
a \div b = c ......{a \% b}
$$
在这个公式中如果 $a\%b = 0$,说明 $(a,b) = b$,如果$a \% b \ne 0$,则进行赋值$a:= b,b:= a \% b$,继续进行辗转相除,直至得到 $a\% b=0$ 。
代码
int gcd(int a, int b){
return a % b ? gcd(b, a % b) : b;
}
欧拉函数
欧拉函数概念
给定一个正整数 $N$ ,欧拉函数 $\phi(N)$ 即为 $[1, N]$ 中与 $N$ 互质的数的个数。$p_i$ 为质数, $c_i$ 为次数:
$$
N = \prod p_i ^ {c_i}
$$
那么:
$$
\phi(N) = N·\prod\frac{p_i - 1}{p_i}
$$
代码
int phi(int n){
int ans = n;
for (int i = 2; i <= n / i; i ++ ){
if (n % i == 0){
ans = ans / i * (i - 1);
while (n % i == 0)
n /= i;
}
}
if (n > 1) ans = ans / n * (n - 1);
return ans;
}
筛法求欧拉函数
对于每个数 $N$ ,借助线性筛,欧拉函数可以用递推公式推出,下面分类讨论:
-
$N$ 为质数:
此时 $N$ 与其他不是他本身的数都互质,也就是说:
$$ \phi(N) = N - 1 $$ -
$N$ 不为质数:
假设 $ N = p ·s$,其中 $p$ 为质数,那么又分类讨论:
a. $p \mid s$ 时,说明 $s$ 中已经含有质因子 $p$ ,所以此时:
$$ \phi(N) = \phi(p·s) = p·\phi(s) $$
b. $p \nmid s$ 时,说明 $s$ 中不会含有质因子 $p$ ,所以此时:
$$
\phi(N) = \phi(p·s) = p·\phi(s)·\frac{p -1}{p} = \phi(s)·(p - 1)
$$
代码
void getPhi(int n){
for (int i = 2; i <= n; i ++ ){
if (!vis[i]){
primes[cnt ++ ] = i;
phi[i] = i - 1;
}
for (int j = 0; primes[j] <= n / i; j ++ ){
vis[i * primes[j]] = 1;
if (i % primes[j] == 0){
phi[i * primes[j]] = primes[j] * phi[i];
break;
}
phi[i * primes[j]] = (primes[j] - 1) * phi[i];
}
}
}
快速幂
快速幂模板
给定 $a, b$ 算出 $a ^ b$ 的结果。
传统方法是直接将 $a$ 乘 $b$ 次,但是算法复杂度是 $O(b)$,如果遇到 $b$ 很大的情况就很慢。
下面是快速幂的作用原理:
假设 $b$ 是偶数,那么:
$$
a^b = a ^ {2\frac{b}{2}} = (a^2)^{\frac{b}{2}}
$$
也就是说,将 $a$ 重新赋值为 $a ^ 2$ ,$b$ 重新赋值为 $\frac{b}{2}$。
假设 $b$ 是奇数,那么:
$$
a ^ b = a·a^{b - 1} = a · (a^2)^{\frac{b-1}{2}}
$$
将这个被“挤”出来的 $a$ 给 $res$ 吸收即可。
一直重复上述操作,直至 $b = 0$ 即可结束。时间复杂度降到 $O(\log b)$。
代码
typedef long long ll;
int qmi(int a, int b, int p){
int res = 1;
while (b){
if (b & 1) res = (ll) res * a % p;
b >>= 1;
a = (ll) a * a % p;
}
return res;
}
快速幂求逆元
首先要了解乘法逆元的概念:
给定三个正整数 $a,b,p$,如果满足:
$$ a·b \equiv1\mod p $$
那么 $b$ 称为在 $\mod p$ 的条件下 $a$ 的乘法逆元,记作$a^{-1}$。 注意:不是所有的数在某些模量下都有逆元。
$a$ 存在逆元的充要条件是 $a$ 与 $p$ 互质。
$$ \exists b\in\{x | x \in Z \land x \in[0,p - 1]\},a·b \equiv 1 \mod p \Leftrightarrow (a,p) = 1 $$
同时我们又要了解一些求逆元所用的定理:
欧拉定理:
对于正整数 $a,p$ ,若 $(a, p) = 1$ ( $a$ 与 $n$ 互质)恒有:
$$ a ^ {\phi(p)} \equiv 1 \mod p $$
根据这个定理,我们可以求出这个条件下 $a$ 的逆元:
$$
a^{\phi(p)} \equiv 1 \mod p
$$
$$ a · a^{\phi(p) - 1} \equiv 1 \mod p $$
$$ [a ^ {-1}]_p = [a ^ {\phi(p) - 1}]_p $$
特别的,费马小定理:如果 $n$ 为质数,那么 $\phi(p) = p - 1$,此时:
$$
[a ^ {-1}]_p = [a ^ {p - 2}]_p
$$
代码
int inverse(int a, int p){
return gcd(a, p) == 1 ? qmi(a, p - 2, p) : -1;
}
欧几里得算法
扩展欧几里得算法
给定一对正整数 $a,b$,求出一组 $x,y$,使其满足:
$$
a · x + b · y = (a, b)
$$
贝祖定理:
有一个线性不定方程
$$ ax+by=c $$
若此方程有解,那么
$$ c=k·(a,b) ,k \in Z^+ $$
如何求解这个线性不定方程:
我们知道最大公因数的求解方法,所以这个方程可以写成如下形式:
$$
ax+by=(a,b)=(b, a\%b)=bx’+a\%by’\\
$$
$$ a\%b=a-\lfloor\frac{a}{b}\rfloor·b\\ $$
$$ ax+by=bx’+(a-\lfloor\frac{a}{b}\rfloor·b)y’\\ $$
$$
ax+by=ay’+b·(x’-\lfloor\frac{a}{b}\rfloor·y’)
$$
对比系数,可得:
$$
x=y’\\
$$
$$
y=x’-\lfloor\frac{a}{b}\rfloor·y’
$$
由此可知,我们可以通过递归的思想来求出符合的一组解。
递归边界:当 $b = 0$ 时,$(a,b)=a,x=1,y\in Z$
特别的,用扩展欧几里得算法还可以求出乘法逆元。
$$
ax\equiv 1 \mod p\\
$$
$$
ax+py=1
$$
当且仅当 $(a,p) = 1$ 时有解。
代码
int exgcd(int a, int b, int &x, int &y){
if (!b){
x = 1, y = 0;
return a;
}
int d = exgcd(b, a % b, y, x);
y -= a / b * x;
return d;
}
线性同余方程
给定 $a,b,p$ ,求出 $x$ 使其满足
$$
a·x\equiv b\mod p
$$
这个方程可以写为
$$
ax+py=b
$$
要使该方程有解,则满足
$$
b=k·(a,p),k\in Z
$$
用扩展欧几里得算法求出 $ax+py=(a,p)$ 的 $x$ 的解之后,再将 $x$ 乘上 $\frac{b}{(a,p)}$即可。
代码
void solve(int a, int b, int p){
int x, y;
int d = exgcd(a, p, x, y);
if (b % d) cout << "impossible";
else
cout << x * b / d % p;
}
中国剩余定理
概念
给定一组线性同余方程组,求出 $x$ 最小非负整数解:
$$
x \equiv a_1 \mod p_1\\
$$
$$ x \equiv a_2 \mod p_2\\ $$
$$ \vdots\\ $$
$$ x \equiv a_n \mod p_n $$
中国剩余定理:
令 $M = \prod m_i$
则
$$ x \equiv \sum c_i · \frac{M}{m_i} · [\frac{M}{m_i}]^{-1}_{m_i} \mod M $$
求解线性同余方程组的一种方法
首先考虑前两个线性同余方程:
$$
x \equiv a_1 \mod p_1\\
$$
$$
x \equiv a_2 \mod p_2\\
$$
分别可以写成:
$$
x = p_1 \cdot k_1 + a_1\\
$$
$$
x = p_2 \cdot k_2 + a_2\\
$$
将这两个方程合并移项,可得:
$$
p_1 \cdot k_1 - p_2 \cdot k_2 = a_2 - a_1
$$
暂且把负号吸收到 $k_2$ 中,得:
$$
p_1 \cdot k_1 + p_2 \cdot k_2 = a_2 - a_1
$$
将 $k_1,k_2$看做这个等式的变量,并用贝祖定理 + 扩展欧几里得算法来判断是否有解。如果有解,则继续往下走。
通过扩展欧几里得算法算出 $d=(p_1,p_2)$
此时我们可以求出 $k_1$ 的通解:
$$
k_1’ = k_1 \cdot \frac{a_2 - a_1}{d} + \frac{p_2}{d} \cdot k,k\in Z
$$
将 $k_1’$ 代入 $k_1$
$$
x = p_1 \cdot k_1 + a_1
$$
得:
$$
x = (k_1 \cdot \frac{a_2 - a_1}{d} + \frac{p_2}{d} \cdot k) \cdot p1 + a_1
$$
整理得:
$$
x = \frac{p_1 p_2}{d} \cdot k + a_1 + k_1 \cdot \frac{a_2 - a_1}{d} \cdot a_1
$$
可以发现这个方程形似上述的方程
$$
x=p \cdot k + a
$$
这时候可以对比各数:
$$
p = \frac{p_1p_2}{d}\\
$$
$$
a = a_1 + k_1 \cdot a_1 \cdot \frac{a_2 - a_1}{d}
$$
将得到的方程与下一个方程继续合并直到只剩下一个方程:
$$
x = p \cdot k + a\\
$$
$$ x = p_3 \cdot k_3 + a_3\\ $$
$$
\vdots
$$
得到最后的方程:
$$
x = p’ \cdot k’ + a’
$$
因为要求最小非负整数解,故:
$$
x = a’ \mod p’
$$
代码
ll solve(vector<int> a, vector<int> p){
int n = a.size();
ll p1 = p[0], a1 = a[0];
for (int i = 1; i < n; i ++ ){
ll p2 = p[i], a2 = a[i], k1, k2;
ll d = exgcd(p1, p2, k1, k2);
if ((a2 - a1) % d)
return -1;
k1 *= (a2 - a1) / d;
k1 = mod(k1, p2 / d);
a1 += k1 * p1;
p1 *= p2 / d;
}
return mod(a1, p1);
}
高斯消元
高斯消元求解线性方程组
我们求解一组线性方程的方法就是高斯消元法。
这个概念学过 线性代数 的朋友都应该了解到。
将方程组化为增广矩阵形式,通过初等变换(交换行,翻倍,行减法)将其化为阶梯矩阵并求解。
代码
void gauss(){
int r, c;
for (r = 0, c = 0; c < n; c ++ ){
int t = r;
for (int i = r + 1; i < n; i ++ )
if (fabs(a[i][c]) > fabs(a[t][c])) //找出绝对值最大的主元
t = i;
if (fabs(a[t][c]) < Eps) continue; //如果这个主元为 0 则跳过
for (int i = n; i >= c; i -- ) //将主元所在的行挪到行r
swap(a[t][i], a[r][i]);
for (int i = n; i >= c; i -- ) //将主元所在的行都缩小主元的倍数
a[r][i] /= a[r][c];
for (int i = r + 1; i < n; i ++ ) // 消元
for (int j = n; j >= c; j -- )
a[i][j] -= a[i][c] * a[r][j];
r ++ ; //行数+1
}
if (r < n){
if (fabs(a[r][n]) > Eps){ //无解
cout << "No solution";
return ;
}
cout << "Infinite group solutions"; //无穷解
return ;
}
for (int i = n - 2; ~ i; i -- ){ //唯一解
for (int j = i + 1; j < n; j ++ )
a[i][n] -= a[j][n] * a[i][j];
}
for (int i = 0; i < n; i ++ ) //输出解
printf("%.2lf\n", a[i][n]);
return ;
}
求解异或线性方程组
用高斯消元法,符号换成异或符号 $\oplus$ 。
代码
void gauss(){
int r, c;
for (r = 0, c = 0; c < n; c ++ ){
int t = r;
for (int i = r; i < n; i ++ )
if (a[i][c]){
t = i;
break;
}
if (!a[t][c]) continue;
for (int i = n; i >= c; i -- )
swap(a[t][i], a[r][i]);
for (int i = r + 1; i < n; i ++ )
if (!a[i][c]) continue;
else
for (int j = n; j >= c; j -- )
a[i][j] ^= a[r][j];
r ++ ;
}
if (r < n){
if (a[r][n]){
cout << "No solution";
return ;
}
cout << "Multiple sets of solutions";
return ;
}
for (int i = n - 2; ~ i; i -- ){
for (int j = i + 1; j < n; j ++ )
if (a[i][j]) a[i][c] ^= a[j][c];
}
for (int i = 0; i < n; i ++ )
cout << a[i][n] << endl;
return ;
}
组合数
给定 $a, b$ ,求
$$
\binom{a}{b} \mod 10^9+7\\
$$
$$ C_{a}^{b} \mod 10^9+7\\ $$
模板1:$O(N^2)$
原理:预处理组合数
$$
\binom{a}{b} = \binom{a-1}{b} + \binom{a-1}{b-1}\\
$$
$$ \binom{x}{0} = 1\\ $$
$$ C_a^b = C_{a-1}^{b} + C_{a-1}^{b-1}\\ $$
$$
C_{x}^{0} = 1
$$
代码
void init(){
for (int i = 0; i < N; i ++ )
for (int j = 0; j <= i; j ++ )
C[i][j] = !j ? 1 : (C[i - 1][j] + C[i - 1][j - 1]) % Mod;
}
模板2:$O(N)$
原理:预处理阶乘
$$
\binom{a}{b}=C_{a}^{b}=\frac{a!}{b!(a-b)!} \mod p\\
$$
$$
\frac{1}{b!}=[b!]_{p}=(b!)^{p-2} \mod p
$$
因为这是在 $\mod 10^9+7$ 下的乘法运算,所以需要用乘法逆元。
代码
void init(){
fact[0] = 1;
infact[0] = 1;
for (int i = 1; i < N; i ++ ){
fact[i] = (ll) fact[i - 1] * i % Mod;
infact[i] = qmi(fact[i], Mod - 2, Mod);
}
return ;
}
模板3:大数取模组合数
原理:Lucas定理
$$
\binom{a}{b}=\binom{a \mod p}{b \mod p}\cdot\binom{\lfloor\frac{a}{p}\rfloor}{\lfloor\frac{b}{p}\rfloor}\\
$$
$$
C_{a}^{b}=C_{a \mod p}^{b \mod p}\cdot C_{\lfloor \frac{a}{p} \rfloor}^{\lfloor\frac{b}{p}\rfloor}\\
$$
代码
ll lucas(ll a, ll b, ll p){
if (a < p and b < p) return C(a, b, p);
return lucas(a / p, b / p, p) * C(a % p, b % p, p) % p;
}
模板4:高精度
原理:将组合数转化为一系列的质数的乘积
$$
\binom{a}{b} = \frac{a!}{b!(a - b)!} = \prod p_i^{c_i}
$$
从这个公式可以在阶乘中分解得到每个质因数的次数。
在阶乘 $a!$ 中,我们如何获得质因子 $p$ 的次数。
首先考虑 $p$ 的倍数 $p, 2p, 3p \cdots$,可知 $p$ 的倍数有 $\lfloor\frac{a}{p}\rfloor$ 个。
再考虑 $p^2$ 的倍数 $p^2, 2p^2, 3p^2\cdots$,可知 $p^2$ 的倍数有 $\lfloor\frac{a}{p^2}\rfloor$ 个。
以此类推。
这些倍数中可能会有与上一个次数的有重复,也就是 $p^2$ 与 $p$ 可能会有重复的,但没有关系,我们只需要把$\lfloor\frac{a}{p^i}\rfloor$都加一次就行了,避免重复。下面写get()函数来获取阶乘 $x!$ 中的 $p$ 的次数。
代码
int get(int x, int p){
int res = 0;
while (x){
res += x / p;
x /= p;
}
return res;
}
高精度 $\times$ 低精度,重载运算符即可。
typedef vector<int> vi;
vi operator * (vi a, int b){
int pro = 0;
for (int i = 0; i < a.size(); i ++ ){
a[i] = a[i] * b + pro;
pro = a[i] / 10;
a[i] %= 10;
}
while (pro){
a.push_back(pro % 10);
pro /= 10;
}
return a;
}
转换成一系列质因子的乘积
typedef vector<int> vi;
vi result(int a, int b){
vi primes = getPrimes(a);
vi res;
res.push_back(1);
int cnt = primes.size();
for (int i = 0; i < cnt; i ++ ){
int p = primes[i];
int sum = get(a, p) - get(b, p) - get(a - b, p);
while (sum -- )
res = res * p;
}
return res;
}
满足条件的01序列(组合例题)
给定 $n$ 个 $0$ 和 $n$ 个 $1$ ,它们将按照某种顺序排成长度为 $2n$ 的序列,求它们能排列成的所有序列中,能够满足任意前缀序列中 $0$ 的个数都不少于 $1$ 的个数的序列有多少个。
输出的答案对 $10^9+7$ 取模。
卡特兰数
是一种很经典的组合数,通项公式:
$$
C_n = \binom{2n}{n}-\binom{2n}{n-1} = \frac{1}{n + 1}\binom{2n}{n}
$$
一般能解决的四类应用:
-
括号化问题:分别给定 $n$ 个左括号和右括号,求出括号正确匹配方法有多少。
-
出栈次序问题:给定 $n$ 个元素,分别进行入栈出栈操作,求出栈后的次序有多少种。
-
多边形划分三角形问题:给定凸 $n$ 边形,求出将其都分为三角形的方法有多少。
-
给顶节点组成二叉树问题:给定 $n$ 个节点,能构成多少种形状不同的二叉树。
我们可以将此题化为括号化问题,将 $0$ 看作左括号, $1$ 看作右括号。既得答案为第 $n$ 个卡特兰数。
代码
typedef long long ll;
int catalan(int n, int p){
int res = 1;
for (int i = 2, j = 2 * n; i <= n; i ++ , j -- )
res = (ll) res * j % p * qmi(i, p - 2, p);
return res;
}
容斥原理
能被整除的数
给定一个整数 $n$ 和 $m$ 个不同的质数。求出 $[1,n]$ 能被这些质数中至少一个数整除的数的个数。
容斥原理:
给定 $n$ 个不同的集合 $A_i$,集合之间可能会有重复,求出
$$ \vert\bigcup A_i\vert $$
先从两个集合开始考虑,其结果为:
$$ |A_1| + |A_2| - |A_1 \cap A_2| $$
再考虑三个集合,其结果为:
$$ |A_1|+|A_2|+|A_3|-|A_1 \cap A_2|-|A_1 \cap A_3|-|A_2 \cap A_3|+|A_1\cap A_2 \cap A_3| $$
将这些情况推广到一般,可以发现其结果为: 加上所有奇数个集合交集的基数,减去所有偶数个集合交集的基数。
由此我们可以将各质因子看作集合,此时 $|A_i| = \lfloor\frac{n}{p_i}\rfloor$,$|A_i \cap A_j|=\lfloor\frac{n}{p_ip_j}\rfloor$其他情况同样的道理。再用状态压缩来枚举质数的选取方法,根据选取质数个数来判断加减。
代码 $O(2^m)$
typedef long long ll;
int solve(vector<int> primes, int n){
int m = primes.size();
int res = 0;
for (int i = 1; i < 1 << m; i ++ ){
int cnt = 0, t = 1;
for (int j = 0; j < m; j ++ ){
if (i >> j & 1){
cnt ++ ;
if ((ll) t * primes[j] > n){
cnt = -1;
break;
}
t *= primes[j];
}
}
if ( ~ cnt){
res += (cnt & 1 ? 1 : -1) * n / t;
}
}
return res;
}
博弈论
Nim游戏
概念
博弈论的一种最经典的模型。
条件:
有两名玩家。
两名玩家交替移动。
- 能移动的方法只取决于局面。
- 无法进行合法移动的回合即为轮到这个回合的玩家为负。
拿石头
给定 $n$ 堆石子,两位玩家轮流操作,每次操作可以从任意一堆石子中拿走任意数量的石子,最后无法操作的人视为失败。
问如果两人都采用最优策略,先手是否必胜。
先说结论:这 $n$ 堆石子的数量分别为 $a_i$ ,如果 $\bigoplus_{i = 1}^{n}a_i \neq 0$ ,则先手必胜,反之必败。
证明:
定义P-position 和 N-position。
直观地说,P-position指的是必败局面,N-position指的是必胜局面。
严谨的说,无法进行任何操作的局面是P(terminal position),可以操作到P的局面是N,任何操作都会进入N的局面是P。
根据定义,证明一种判断局面的性质的方法的正确性,只需要证明三个命题:
所有terminal position 判为P。
N一定可以操作到P。
P无法移动到某个P。
因为terminal position 只有一个,就是全0,异或仍然是0,所以命题一是显然的。
对于某个局面$(a_1, a_2,\cdots,a_n)$,若$\bigoplus_{i = 1}^{n}a_i \neq 0$,一定存在某个合法操作将其变为 $0$ 。不妨设$\bigoplus_{i = 1}^{n}a_i = k\neq0$ ,则一定存在某个 $a_i$ 他的二进制表示在 $k$ 的最高位上 是 $1$ (否则 $k$ 的最高位的 $1$ 是怎么来的),这时 $a_i\oplus k < a_i$ 一定成立,也就是说这个操作可以使 $a_i$ 变小,是合法操作。此时 $\bigoplus_{i = 1}^{n}a_i \oplus k = 0$,命题二成立。
对于某个局面 $(a_1,a_2,\cdots,a_n)$ ,若$\bigoplus_{i = 1}^{n}a_i = 0$,不存在合法操作,使$\bigoplus_{i = 1}^{n}a_i \oplus k = 0$,此时 $k=0$,非法操作,命题三成立。
所以可以通过结论来用代码实现
void solve(vector<int> a){
int res = 0;
for (auto it : a)
res ^= it;
cout << (res ? "Yes" : "No");
}
阶梯
给定 $n$ 阶台阶,每阶都有若干哥石头,第 $i$ 阶有 $a_i$ 个石子。
两位玩家轮流操作,每次操作可以从任意一级台阶上那若干个石子放到下一级台阶中。
已经拿到地面上的石子不能再拿,最后无法进行操作的人视为失败。
问如果两人都采用最优策略,先手是否必胜。
解法:考虑奇数台阶,奇数台阶上的石头都可以从偶数台阶上获得,也可以流入到偶数台阶上。这就可以用拿石头来考虑:拿走 = 在奇数台阶上流入若干石子到下一个偶数台阶上。
那么 P 即为奇数台阶上异或和为0,N即为奇数台阶上异或和不为0。在 P 局面的时候,没有任何合法操作进入到 N 局面,即将偶数台阶上的石头移动到奇数台阶上都会导致异或和不为0。在 N 局面时,总有合法操作移动到 P 局面,即能够在奇数台阶上合法的“拿走”,使其异或和为0 。
综上所述,奇数台阶上的异或和不为0即先手必胜,反之必败。
代码
void solve(vector<int> a){
int res = 0;
for (int i = 0; i < a.size(); i ++ )
res ^= (i & 1 ? 0 : 1) * a[i];
cout << (res ? "Yes" : "No");
}
集合
给定 $n$ 堆石子,以及 $k$ 种操作(集合 $P$)。
有两名玩家轮流操作,每次操作可以从任意一堆石子种拿去石子,但是拿取的数量只能是 $k$ 种操作中的一种,最后无法进行操作的人视为失败。
问如果两人都采用最优策略,先手是否必胜。
首先了解 $SG(x)$ 函数, $x$ 代表局面,$SG(x)$ 代表由局面 $x$ 的局面序数中能够到达的局面中无法到达的最小的局面序数。其中 $SG(x)=0$ 时代表局面 $x$ 是必败的,也就是无法继续合法的操作的局面。(局面序数是个人不严谨的定义,只为更好的理解。)
直观的说,如果 $x$ 能够到达 $0,1,2$,则$SG(x)=3$。如果 $x$ 能够到达 $1,3,4$,那么 $SG(x)=0$,因为 $x$ 无法到达 $0,2,5,6\cdots$,最小的就是 $0$ 。
最后将所有石子堆的 $SG$ 值异或和起来,不为 $0$ 则必胜,反之必败。
画图举例:(以 $n = 2,4,7$ $k = 2,5$ 为例)
首先考虑 7 个石子的一堆,总共能走的局面如下:
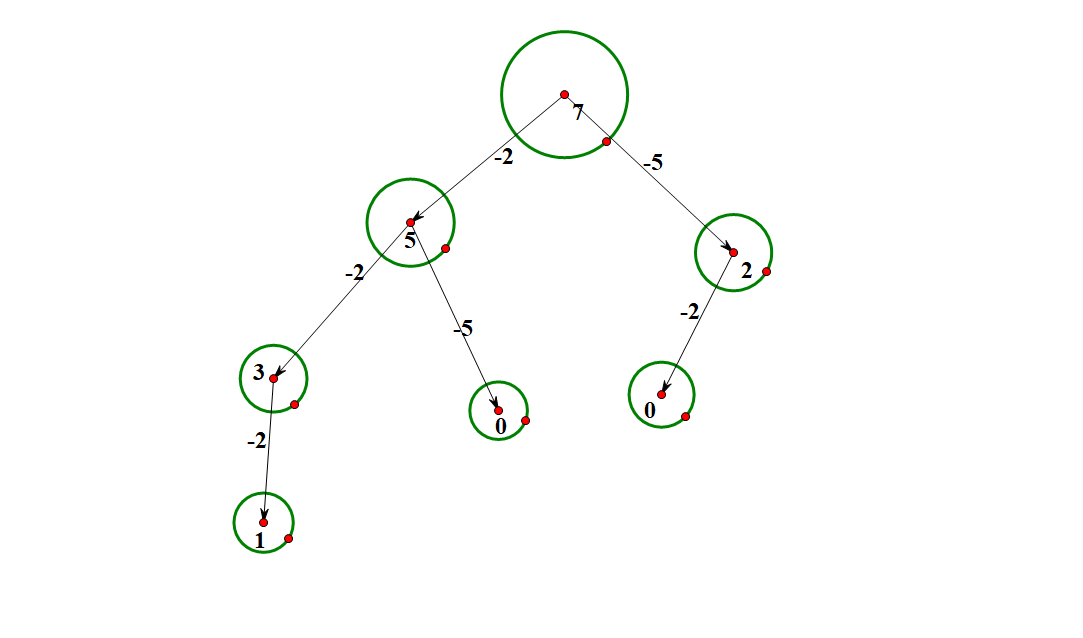
可以看到,所有的叶节点都是无法操作的,也就是 $SG$ 值为 0。$SG(0) = SG(1) = 0$。
再根据 $SG$ 函数的定义,可以推出其他局面的 $SG$ 值。
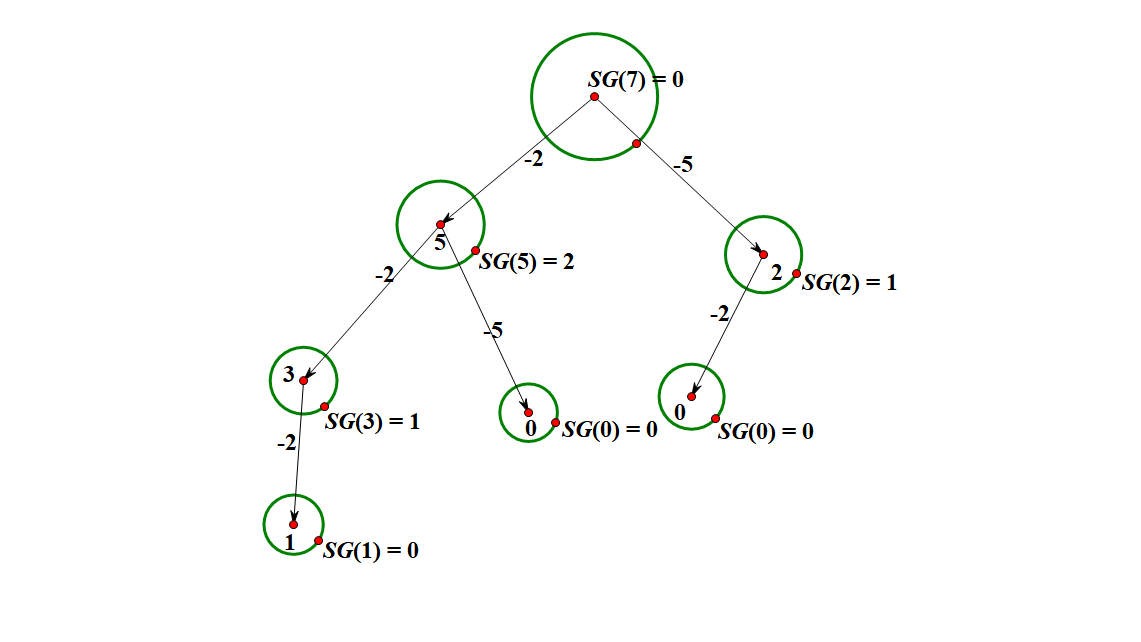
最后将所有石子堆的 $SG$ 值异或起来得到答案。
这个时候可以回顾拿石头,对于每堆石子 $a_i$ 而言,能拿走$[1,a_i]$,也就是说 $a_i$ 局面能够走到 $a_i$ 种局面,也就是有局面序数 $[0,a_i-1]$,所以可以发现对于拿石头而言,$SG(a_i)=a_i$。
代码
typedef vector<int> vi;
int f[N];
int sg(int x, vi P){
if ( ~ f[x]) return f[x]; //记忆化搜索
bool vis[N] = {0};
for (auto it : P){
if (x >= it)
vis[sg(x - it, P)] = 1;
}
for (int i = 0; ; i ++ )
if (!vis[i]) return f[x] = i;
}
int solve(vi a, vi P){
int ans = 0;
for (auto it : a){
ans ^= sg(it, P);
}
return ans;
}
拆分
给定 $n$ 堆石子。
有两名玩家轮流操作,每次操作可以取走一堆,并放入两堆规模更小的石子(可以为0),无法进行合法操作即为失败。
同样利用 $SG$ 函数来解答。
对于一堆石子 $a_i$,总共可以拆分出来 $a_i^2$的种局面,假设都分为了 $x, y$ ,那么:
$$
SG(a_i) = \bigoplus_{0\leq x \leq y < a_i} SG(x) \oplus SG(y)
$$
最后将所有石子堆的 $SG$ 值异或即可。
代码
int sg(int x){
if ( ~ f[x]) return f[x]; //记忆化搜索
bool vis[N] = {0};
for (int i = 0; i < x; i ++ )
for (int j = 0; j <= i; j ++ )
vis[sg(i) ^ sg(j)] = 1;
for (int i = 0; ; i ++ )
if (!vis[i]) return f[x] = i;
}

