学习笔记
树与图的存储及遍历
AcWing 846. 树的重心 AcWing 847. 图中点的层次
// 邻接矩阵
int g[N][N];
// 邻接表
int h[N], e[M], ne[M], idx; // h[]初始化为-1
bool st[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void dfs(int u)
{
st[u] = true;
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if (!st[j]) dfs[j];
}
}
void bfs()
{
queue<int> q;
q.push(1);
st[1] = true;
while (q.size())
{
int t = q.front();
q.pop();
for (int i = h[t]; ~i; i = ne[i])
{
int j = e[i];
if (!st[j])
{
st[j] = true;
q.push(j);
}
}
}
}
拓扑排序
时间复杂度:$ O(n+m) $
int n, m;
int h[N], e[N], ne[N], idx;
int d[N]; // 入度
int q[N], hh, tt = -1;
bool toposort()
{ // 将所有入度为0的点入队
for (int i = 1; i <= n; i++)
if (!d[i])
q[++tt] = i;
while (hh <= tt)
{
int t = q[hh++];
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (--d[j] == 0) q[++tt] = j;
}
}
// 所有点都入队了,说明是有向无环图,存在拓扑序
return tt == n - 1;
}
最短路
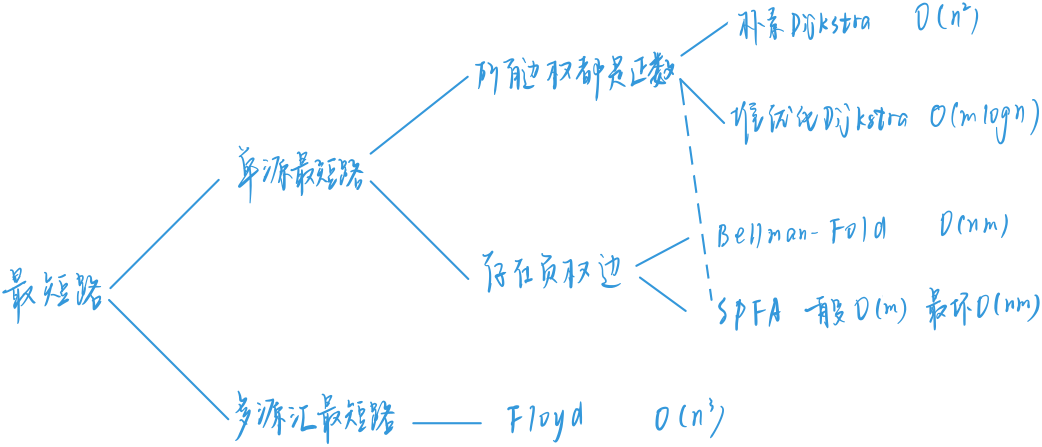
朴素Dijkstra
时间复杂度:$O(n^2+m)$

int g[N][N];
int dist[N];
bool st[N];
int dijkstra()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
for (int i = 0; i < n; i++)
{
int t = -1;
for (int j = 1; i <= n; j++)
if (!st[j] && (t == -1 || dist[j] < dist[t]))
t = j;
st[t] = true;
for (int j = 1; j <= n; j++)
dist[j] = min(dist[j], dist[t] + g[t][j]);
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
堆优化Dijkstra
时间复杂度:$O(mlogn)$
typedef pair<int, int> PII;
int n;
int h[N], w[N], e[N], ne[N], idx;
int dist[N];
bool st[N];
int dijkstra()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
priority_queue<PII, vector<PII>, greater<PII>> heap;
heap.push({0, 1});
while (heap.size())
{
auto t = q.front();
q.pop();
int ver = t.second;
if (st[ver]) continue;
st[ver] = true;
for (int i = h[ver]; ~i; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[ver] + w[i])
{
dist[j] = dist[ver] + w[i];
heap.push({dist[j], j});
}
}
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
Bellman-Ford
时间复杂度:$O(nm)$

int n, m;
int dist[N], backup[N];
struct Edge
{
int a, b, w;
} edges[M];
int bellman_ford()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
for (int i = 0; i < n; i++) // k
{
memcpy(backup, dist, sizeof dist);
for (int j = 0; j < m; j++)
{
int a = edges[j].a, b = edges[j].b, w = edges[j].w;
dist[b] = min(dist[b], backup[a] + w);
}
}
if (dist[n] > 0x3f3f3f3f / 2) return -1;
return dist[n];
}
SPFA
时间复杂度:平均$O(m)$最坏$O(nm)$

int n, m;
int h[N], e[N], w[N], ne[N], idx;
int dist[N];
bool st[N];
int spfa()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
queue<int> q;
q.push(1);
st[1] = true;
while (q.size())
{
int t = q.front();
q.pop();
st[t] = false;
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[t] + w[i])
{
dist[j] = dist[t] + w[i];
if (!st[j])
{
q.push(j);
st[j] = true;
}
}
}
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
SPFA判负环

时间复杂度:$O(nm)$
int n, m;
int h[N], e[M], w[M], ne[M], idx;
int dist[N], cnt[N];
bool st[N];
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
bool spfa()
{
queue<int> q;
for (int i = 1; i <= n; i++)
{
q.push(i);
st[i] = true;
}
while (q.size())
{
int t = q.front();
q.pop();
st[t] = false;
for (int i = h[t]; ~i; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[t] + w[i])
{
dist[j] = dist[t] + w[i];
cnt[j] = cnt[t] + 1;
if (cnt[j] >= n) return true;
if (!st[j])
{
q.push(j);
st[j] = true;
}
}
}
}
return false;
}
Floyd
时间复杂度:$ O(n^3) $
int n, m;
int d[N][N];
void init()
{
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
if (i != j) d[i][j] = INF;
}
void floyd()
{
for (int k = 1; k <= n ; k++)
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
最小生成树
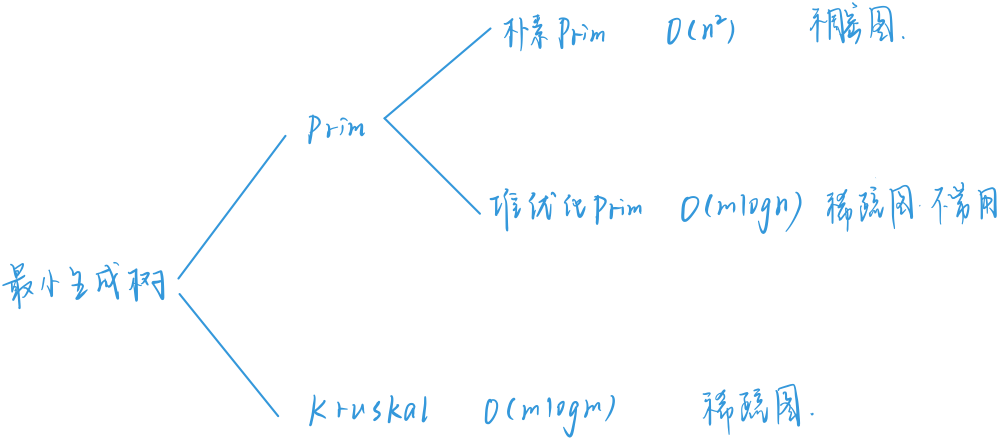
朴素Prim
时间复杂度:$ O(n^2+m) $
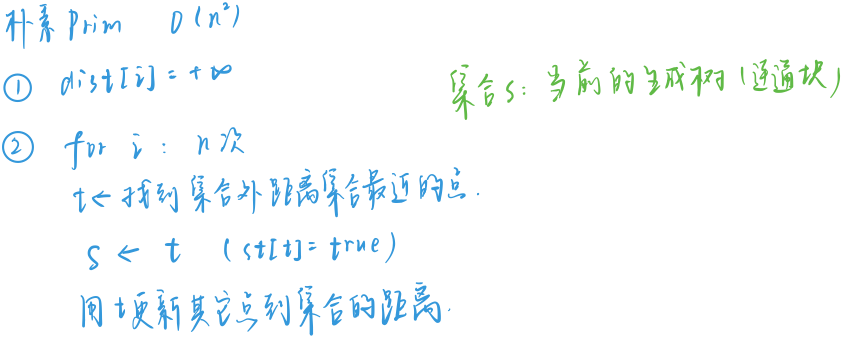
int n, m;
int g[N][N];
int dist[N]; // dist[i]:i到集合的距离
bool st[N];
int prim()
{
memset(dist, 0x3f, sizeof dist);
int res = 0; // 最小生成树的边权之和
for (int i = 0; i < n; i++)
{
int t = -1; // 找到集合外距离集合最近的点
for (int j = 1; j <= n; j++)
if (!st[j] && (t == -1 || dist[j] < dist[t]))
t = j;
// 如果不是第一个点,并且这个点到集合已经不连通了,就返回
if (i && dist[t] == INF) return INF;
// 不是第一个数, 把t加到最小生成树
if (i) res += dist[t];
st[t] = true; // 把t加入集合
// 用t->j的距离,更新集合外的j到集合的距离
for (int j = 1; j <= n; j++)
dist[j] = min(dist[j], g[t][j]);
}
return res;
}
Kruskal
时间复杂度:$ O(mlogm) $
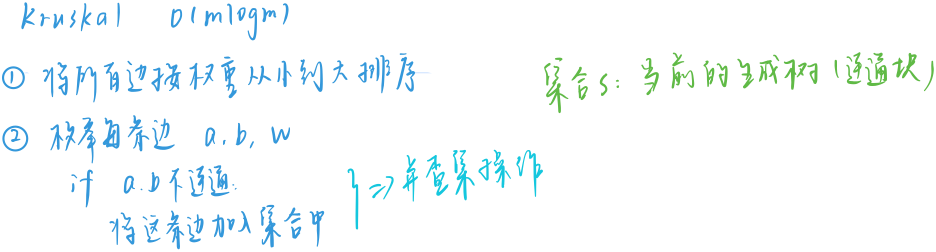
int n, m;
int p[N]; // 并查集的父节点数组
struct Edge
{
int a, b, w;
bool operator< (const Edge &W)const
{
return w < W.w;
}
}edges[M];
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
int kruskal()
{
sort(edges, edges + m);
for (int i = 1; i <= n; i ++ ) p[i] = i; // 初始化并查集
int res = 0, cnt = 0; // res:最小生成树边权之和,cnt:当前加入的边数
for (int i = 0; i < m; i ++ )
{
int a = edges[i].a, b = edges[i].b, w = edges[i].w;
a = find(a), b = find(b);
if (a != b) // 不连通,就把这条边加到生成树里
{ // (并查集初始状态,任意两点之间都是不连通的)
p[a] = b;
res += w;
cnt ++ ;
}
}
if (cnt < n - 1) return INF;
return res;
}
二分图
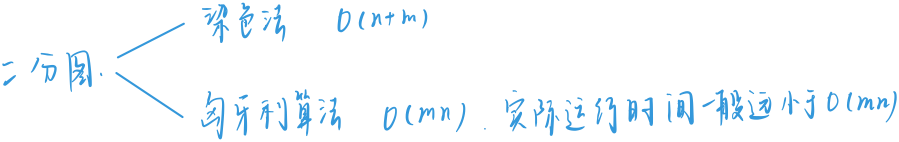
染色法
时间复杂度:$ O(n+m) $
int n, m;
int h[N], e[M], ne[M] ,idx;
int color[N];
// 返回false染色失败,不是二分图
bool dfs(int u, int c)
{
color[u] = c; // 将u染成c
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if (!color[j]) // 如果j未染色
{
if (!dfs(j, 3 - c)) return false; // 染色失败
}
else if (color[j] == c) return false; // 与现有颜色矛盾
}
return true;
}
bool check()
{
for (int i = 1; i <= n; i++)
{
if (!color[i])
if (!dfs(i, 1))
return false;
}
return true;
}
匈牙利算法
时间复杂度:$ O(nm) $
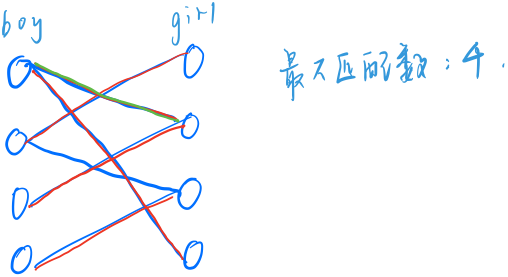
int n1, n2, m;
int h[N], e[M], ne[M], idx;
int match[N]; // match[j]:j号女生匹配的男生
bool st[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
bool find(int x)
{ // 遍历x号男生看上的所有女生
for (int i = h[x]; i != -1; i = ne[i])
{
int j = e[i];
if (!st[j]) // 防止重复匹配
{
st[j] = true; // 标即为匹配过了
if (match[j] == 0 || find(match[j]))
{// 如果j号女生还没有匹配到男生或者她匹配到的男生可以找到下家
match[j] = x; // 就把j匹配给x
return true;
}
}
}
return false;
}
int calc()
{
int res = 0;
for (int i = 1; i <= n1; i++)
{
memset(st, false, sizeof st);
if (find(i)) res++;
}
return res;
}


太棒了~~字真滴好看~~~
字写得真好看
赞一个
赞
厉害! 有其他章节的笔记么,想看看我有哪里记的不够到位~
我边复习边整理的,其他还没整理好,数学和dp整理比较累
我才刚听到图这里(tcl)。看来还要抓紧听了
棒!
hh
字很不错!!!
嘿嘿