RNN（包含困惑度和KL散度与交叉熵的关系推导）

作者： 作者的头像   巷港 ,  2024-08-19 17:41:23 ,  所有人可见 ,  阅读 8

0


首先我们需要明确语言模型language model

语言模型去建模预测给定上下文情况下，下一个单词的概率分布。

n-gram模型

这是经典的语言模型，在dl之前用的一类。n-gram的定义就是连续的n个单词。例如对于the students opened their __这句话，会有1-gram，2-gram…，如下：

7.png

该模型的核心思想是n-gram的概率应正比于其出现的频率，且$P(x^{(t+1)})$ 应该依赖于之前的t个单词。

$$\begin{aligned}&P(x^{(t+1)}|x^{(t)},\ldots,x^{(1)})=P(x^{(t+1)}|x^{(t)},\ldots,x^{(t-n+2)})=\\&\frac{P(x^{(t+1)},x^{(t)},…,x^{(t-n+2)})}{P(x^{(t)},…,x^{(t-n+2)})}\approx\frac{count(x^{(t+1)},x^{(t)},…,x^{(t-n+2)})}{count(x^{(t)},…,x^{(t-n+2)})}\end{aligned}$$

其中count是通过处理大量文本对相应的n-gram出现次数计数得到的。

以实际的例子理解：

8.png

但这类方法有显著的缺点：

  1. 稀疏性：在我们之前的大量文本中，可能分子或分母的组合没有出现过，则其计数为零。并且随着n的增大，稀疏性更严重。但不出现，不代表这种组合是不合理的，也不代表未来不能作为预测的结果。
  2. 我们必须存储所有的n-gram对应的计数，随着n的增大，模型存储量也会增大。

9.png

10.png

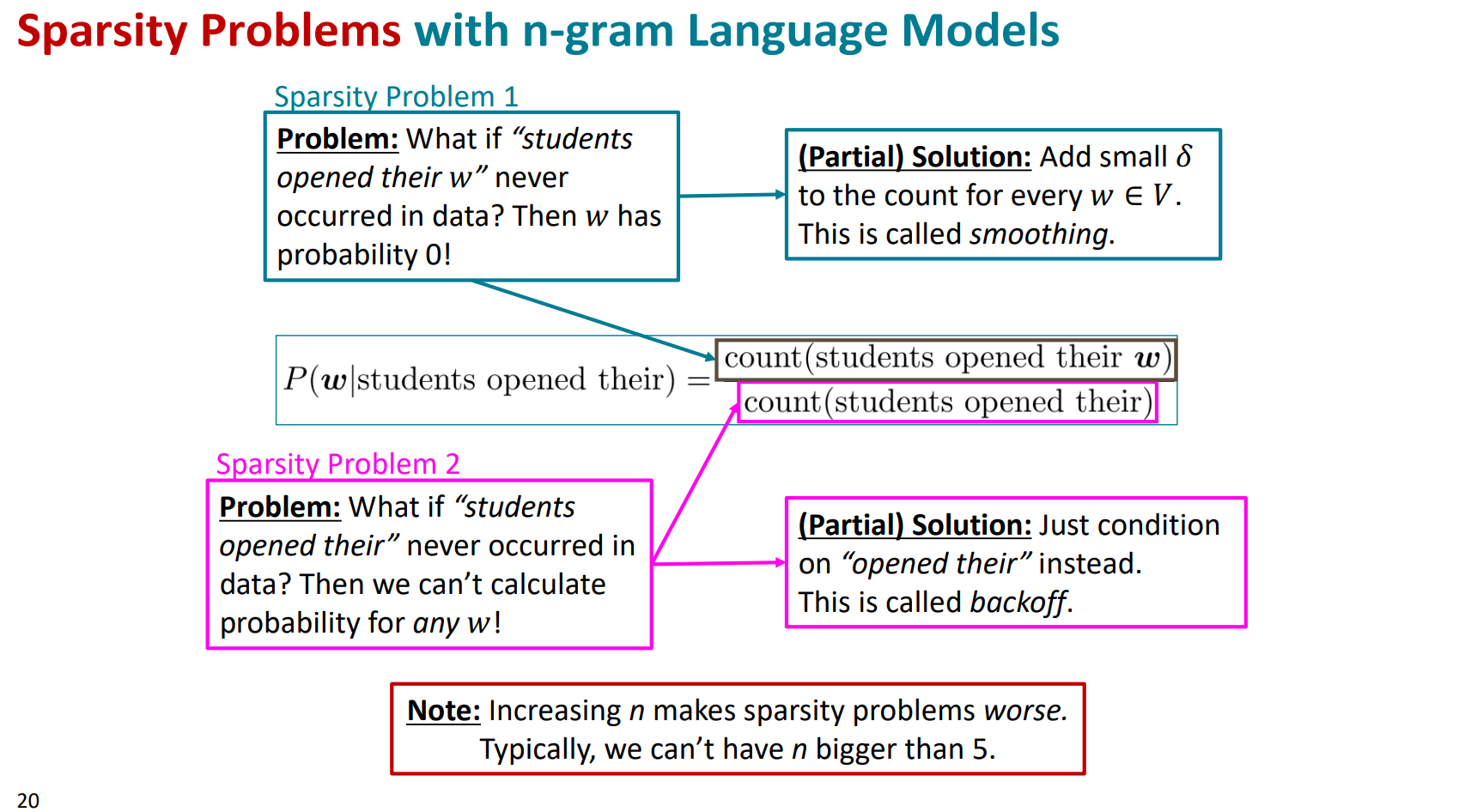
这个问题就是很难受，n小了吧，限制少一些，但是就无法体现稍微远一些的词语对当前词语的影响，这会极大的限制处理语言问题中很多需要依赖相对长程的上文来推测当前单词的任务的能力；n大了吧，又有上述两大限制问题。所以这类模型注定需要被优化。

neural language model

一个想法就是结合之前的word2vec的思想，即基于窗口的dnn。即将定长窗口fixed window中的word embedding连在一起，将其经过神经网络做对下一个单词的分类预测，其类的个数为语裤中的词汇量
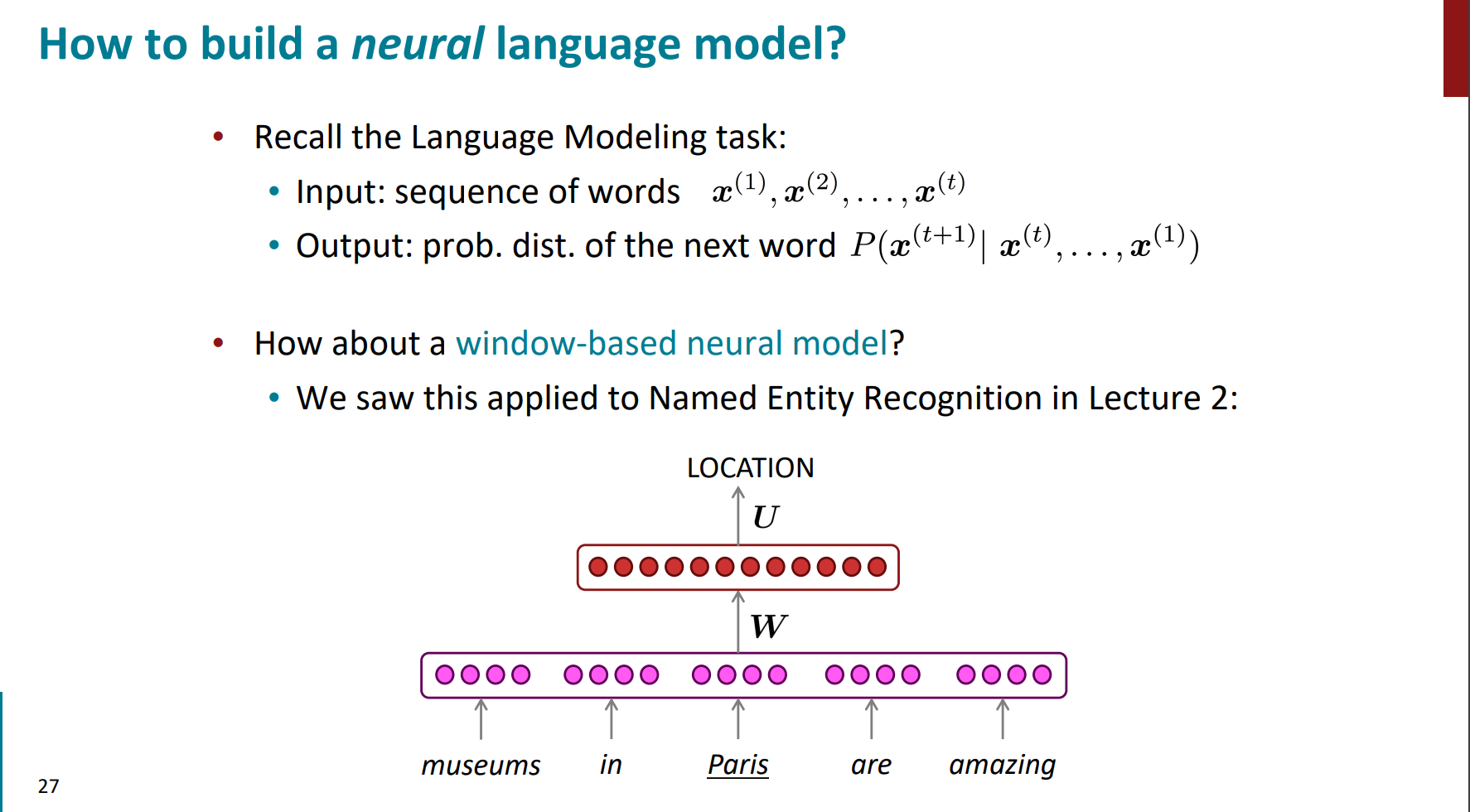
11.png

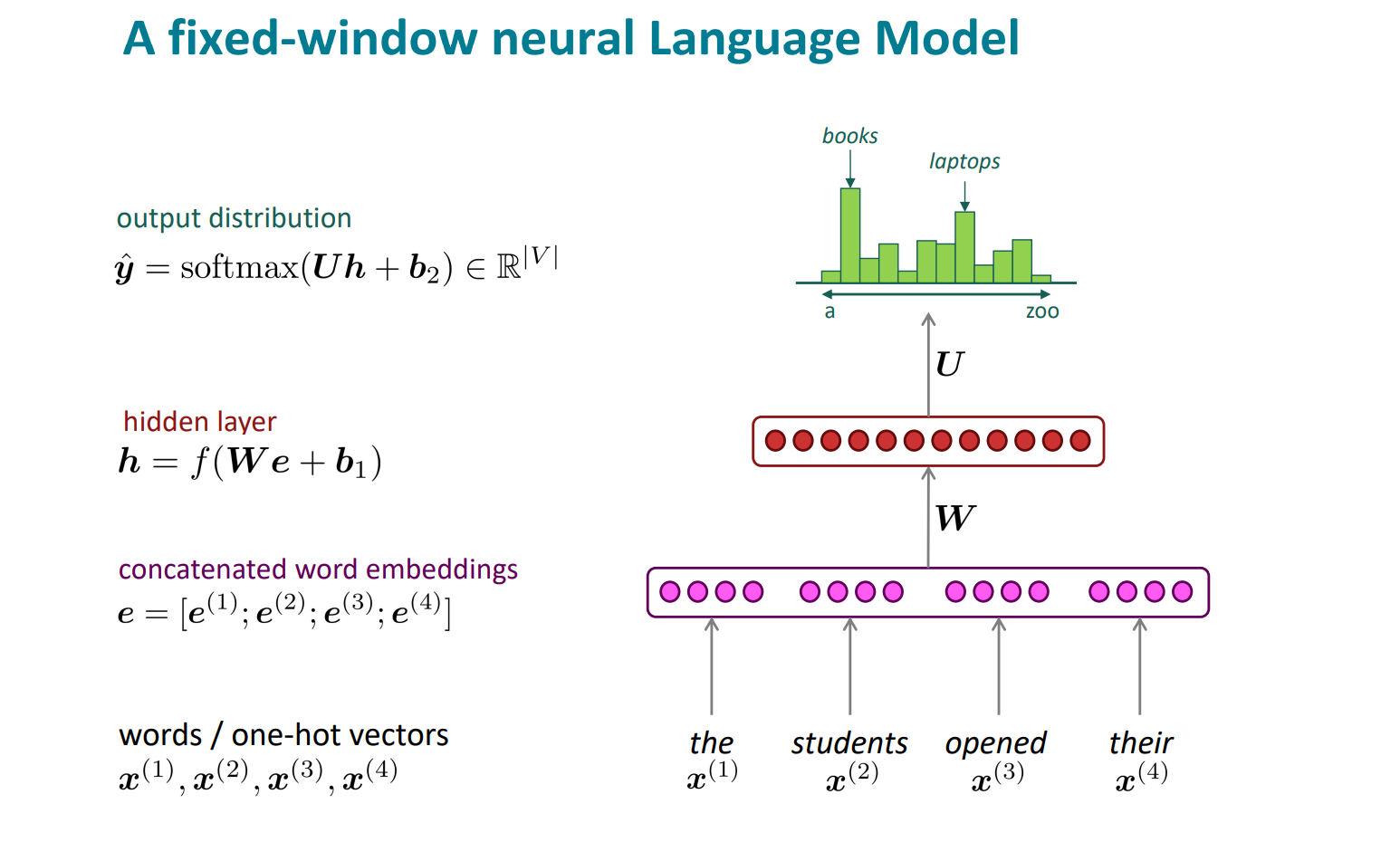
整个的算法过程也很清晰：
1. 输入input
2. 变为嵌入向量embedding vectors
3. 经过隐藏层
4. 输出层用softmax得出概率，类别个数就是词表大小。

12.png

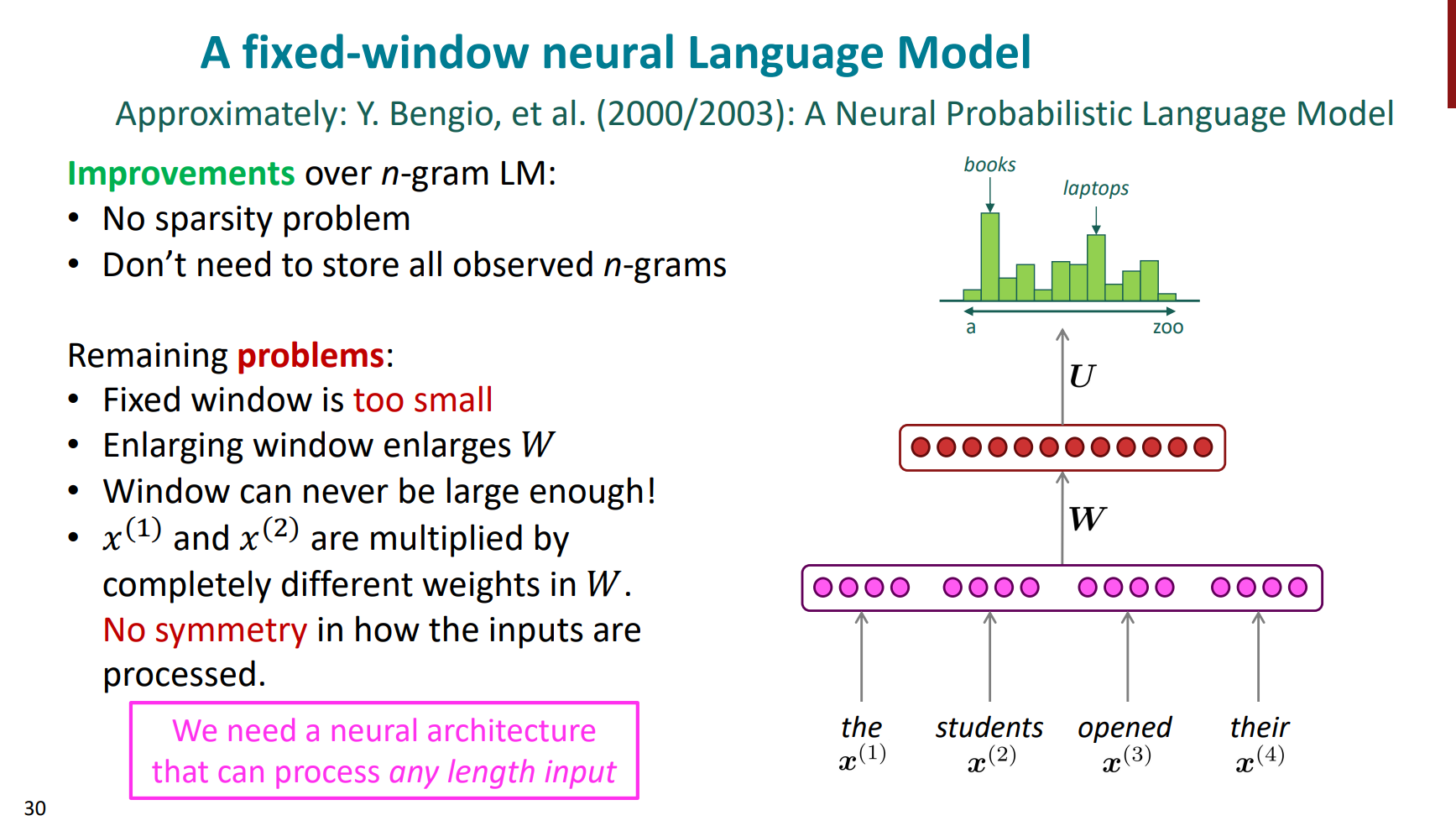
与n-gram模型相比，好处是解决了两大问题，一个是随着n的不断增大的频率稀疏性问题，一个是存储大量的count问题，但是也出现了新的问题：
1. 窗口大小固定，但这个窗口的size太小了，如果变大，那么矩阵W就会随之变大
2. 每一个输入的分量，与权重矩阵W的不同列相乘，参数是独立的，没有共享。

那么我么想做的就是，能让模型处理任意长度的输入，而不是固定窗口大小，比如size=4这样的。

同时，参数可以共享，而不是各自更新各自的。

13.png

那么正式开始RNN

RNN(Recurrent Neural Network)结构通过不断的应用同一个矩阵W可实现参数的有效共享，并且没有固定窗口的限制。其基本结构如下图所示：
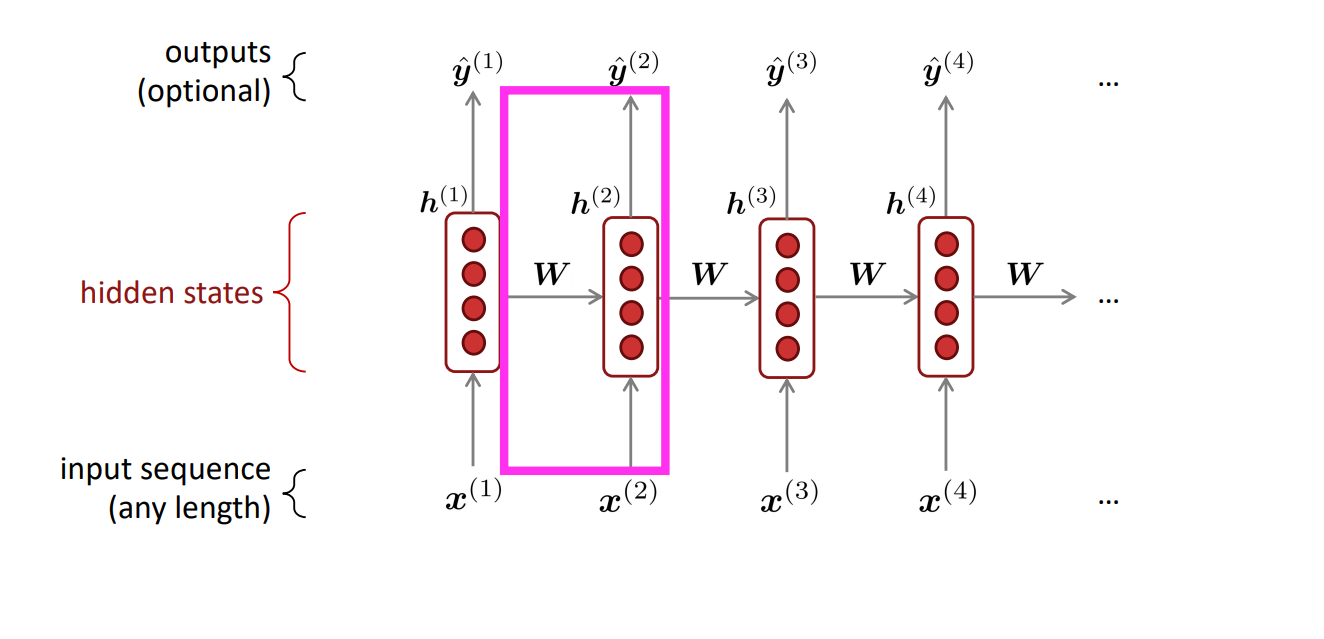
14.png

整个的计算过程就是：
1. 初始的单词vectors，可能是独热编码
2. 得到对应的嵌入词向量
3. 进入hidden states，这里的隐藏层是一个迭代的过程
$$\boldsymbol{h}^{(t)}=\sigma\left(\boldsymbol{W}_h\boldsymbol{h}^{(t-1)}+\boldsymbol{W}_e\boldsymbol{e}^{(t)}+\boldsymbol{b}_1\right)$$
4. 输出层用softmax得到一个概率分布，得到最终答案，即概率最大的word
$$\hat{\boldsymbol{y}}^{(t)}=\operatorname{softmax}\left(\boldsymbol{Uh}^{(t)}+\boldsymbol{b}_2\right)\in\mathbb{R}^{|V|}$$

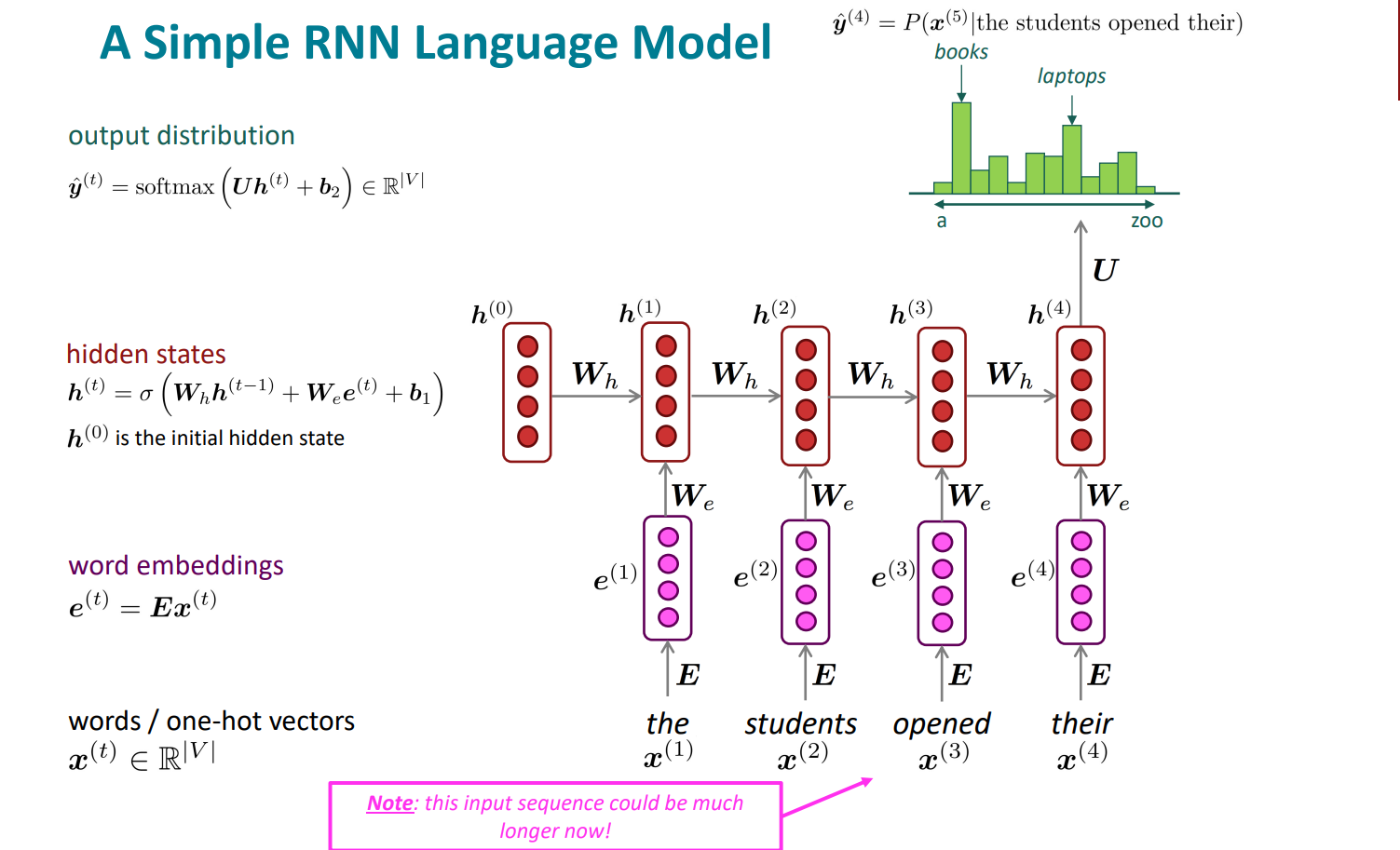
15.png

RNN的优点明显：
1. 可以接受任意长度的input，不用fixed window。
2. 理论上t时刻可以利用之前很早的历史信息。
3. 模型的大小不会随着输入的增长而变大。
4. 每一时刻都采用相同的权重矩阵，有效的进行了参数共享。

但同样RNN的缺点也明显：
1. 计算式串行的，并行能力差，计算慢
2. 长距离的话， 可能会丢失很多信息

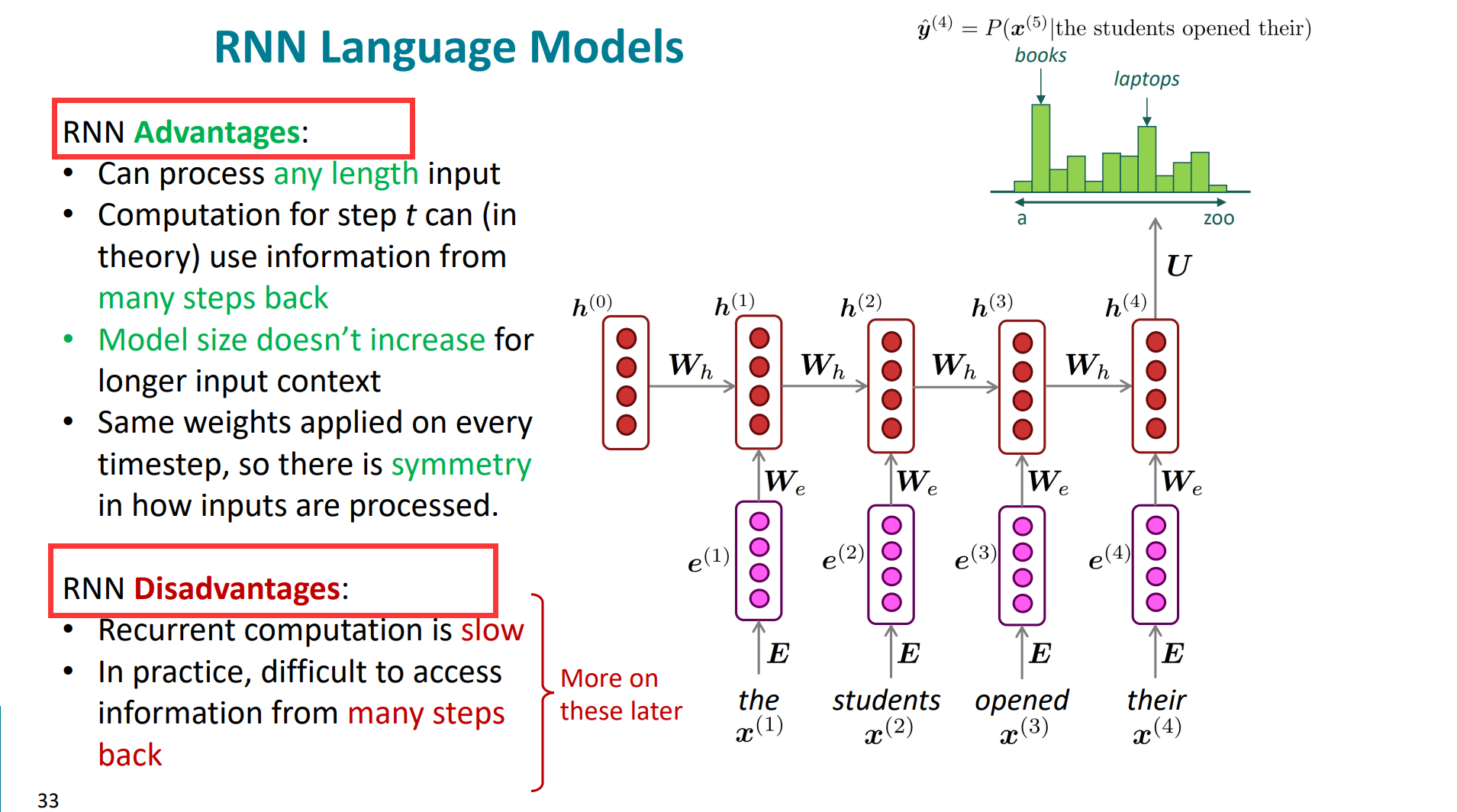
16.png

那么我们开始看具体如何训练一个RNN

整个的过程：
1. 处理语料
2. 把语料集喂进去RNN，根据已有的单词序列，计算每一个时间步长的模型预测分布
3. 计算损失，用交叉熵
4. 平均总和平均交叉熵
22.png

还是以具体例子展开：

第一时间步长：

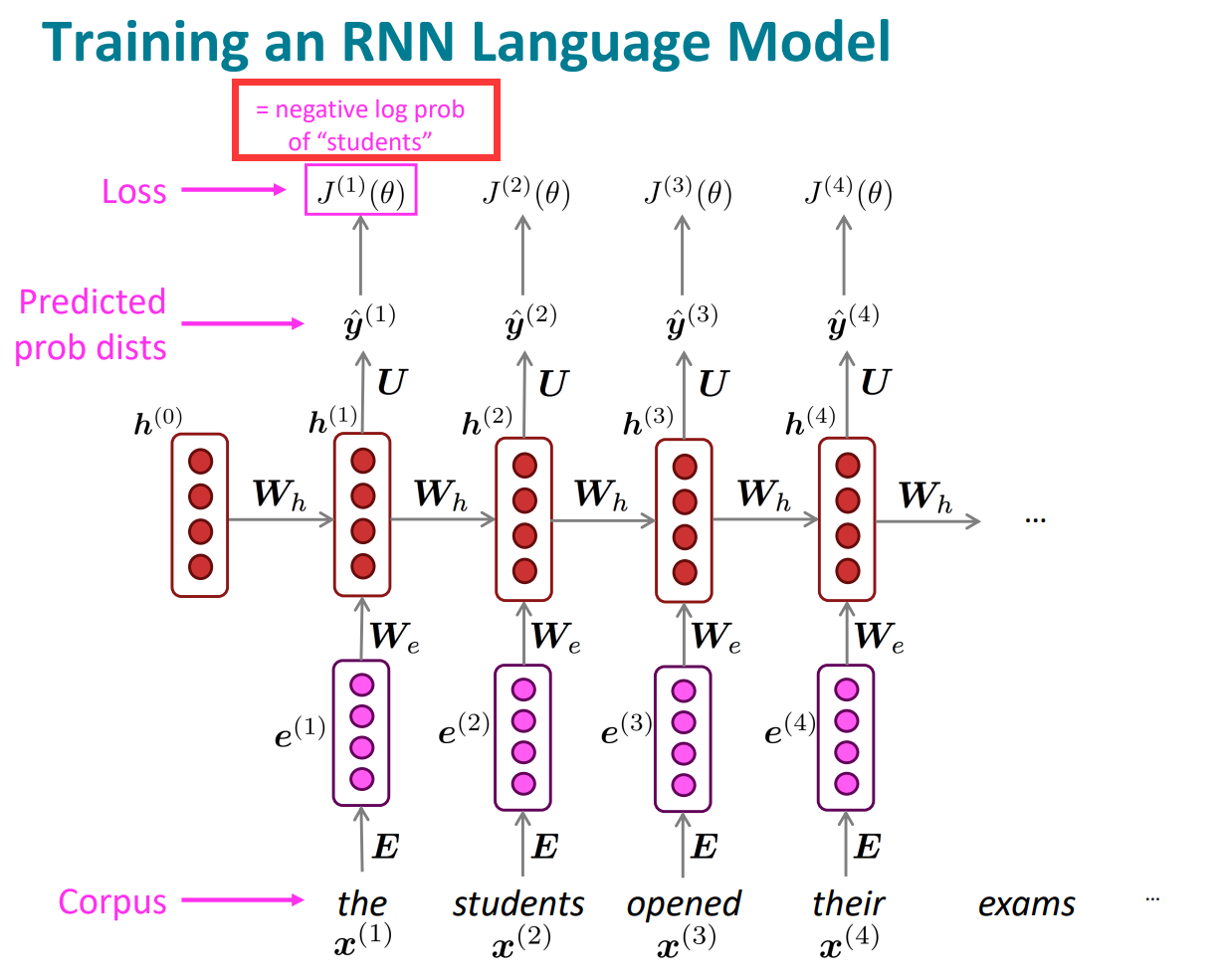
18.png

第二时间步长：

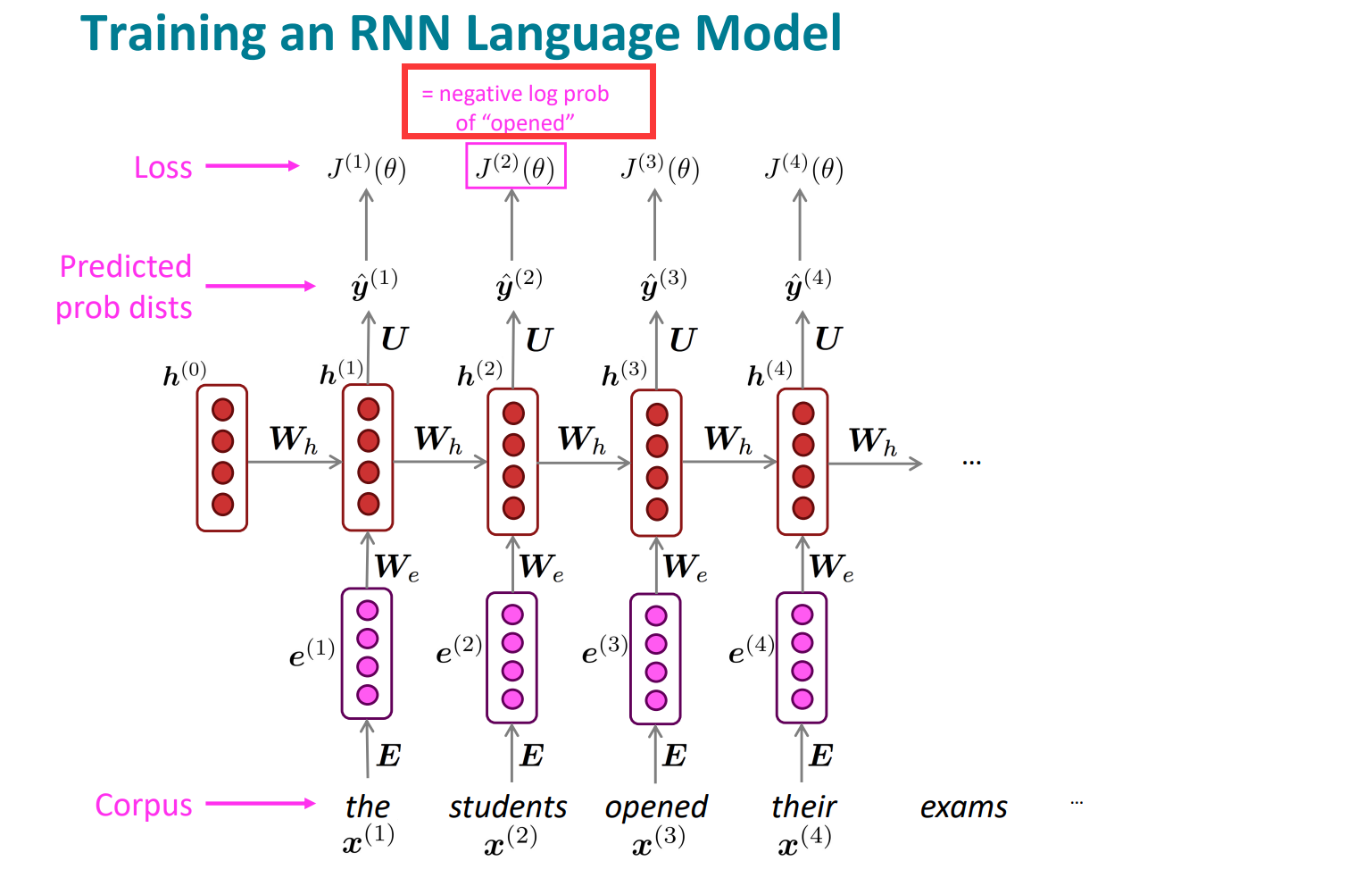
19.png

第三时间步长：

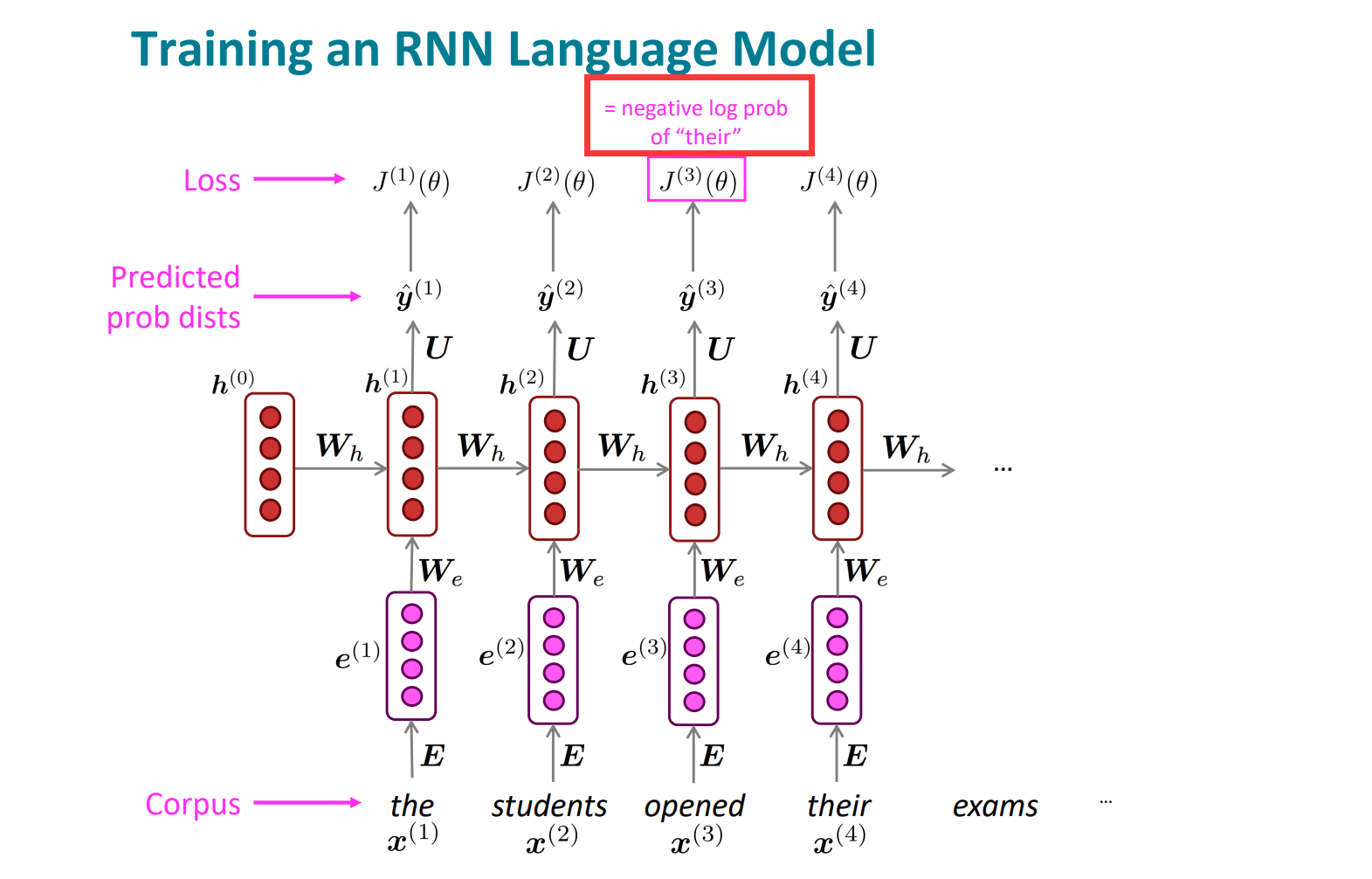
20.png

第四时间步长：

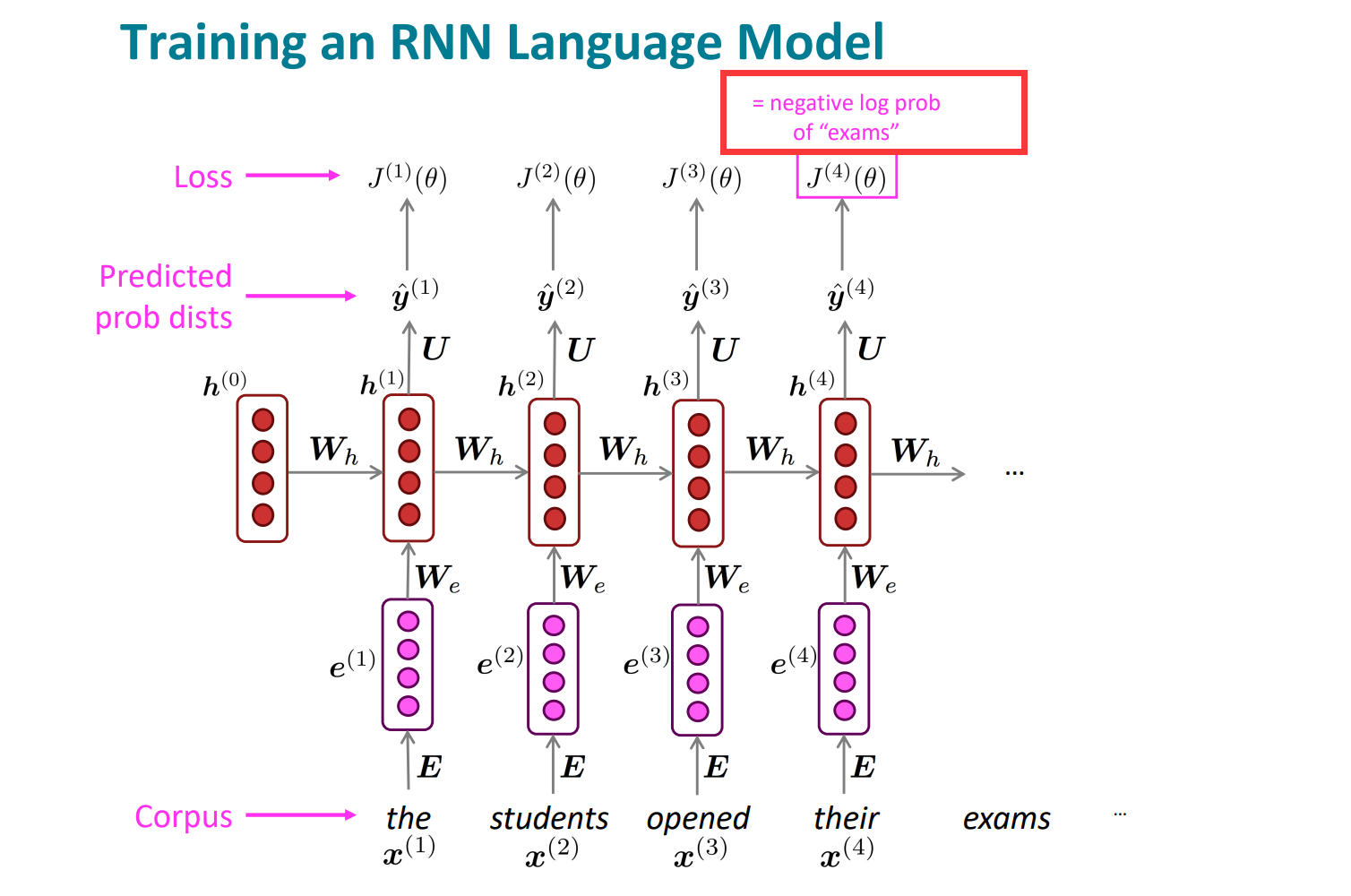
21.png

这里注意有一个细节：

我们是已知当前时间下的当前词是什么的，所以一直是在当前时间步长下，预测下一个位置的词，所以不是竖直方向的一一对应，而是指向下一个。因为要预测下一个位置的时候，当前位置以及前面所有位置的词都是已知的，这也体现出Rnn利用历史信息的能力和优势。

RNN求导

主要参数是矩阵$W_h$，那么求导的结果是各个时间的$W_h$分量之和:

$$\frac{\partial J^{(t)}}{\partial\boldsymbol{W_h}}=\sum_{i=1}^t\frac{\partial J^{(t)}}{\partial\boldsymbol{W_h}}\bigg|_{(i)}$$

那么原因就是链式求导法则，其实也是复合函数求导的。

$$\frac{\partial J^{(t)}}{\partial\boldsymbol{W}_{h}}=\sum_{i=1}^{t}\frac{\partial J^{(t)}}{\partial\boldsymbol{W}_{h}}\bigg|_{(i)}\frac{\partial\boldsymbol{W}_{h}\bigg|_{(i)}}{\partial\boldsymbol{W}_{h}}$$

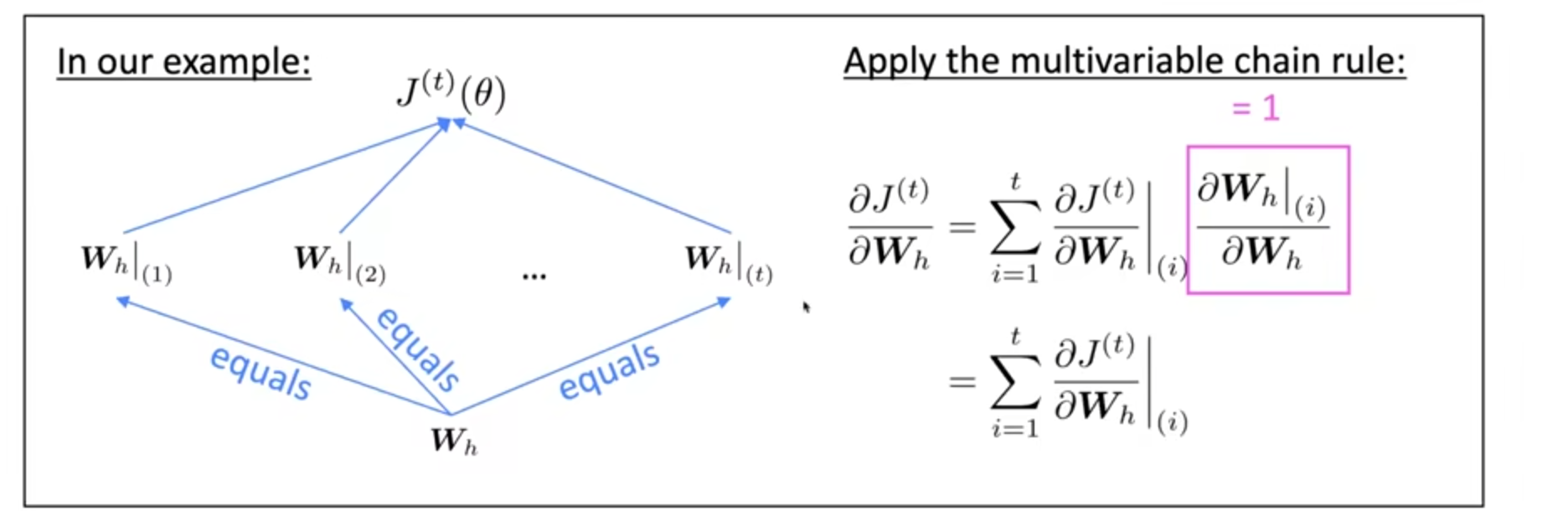
24.png

一般选择截断反向传播，可能选择时间步数为20左右。

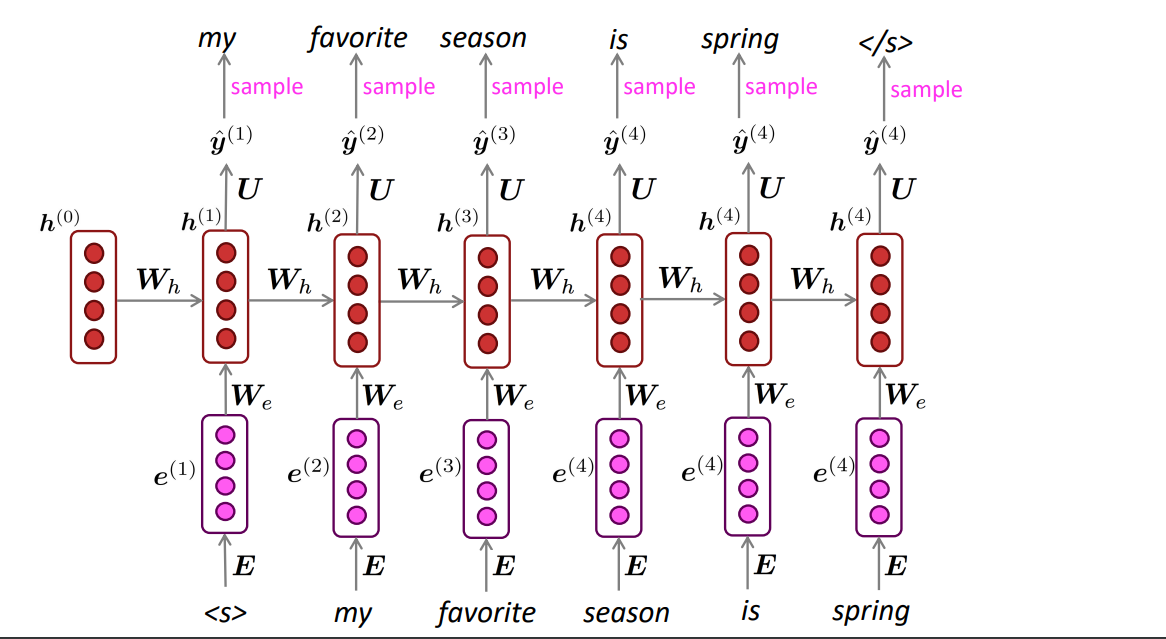
Generating with an RNN Language Model

将sample的output作为下一步的input，重复即可。输入的开始和结束位置是特殊的符号表示。

25.png

接下来是如何评价语言模型好还是不好的指标。

比较经典的一个指标是困惑度perplexity

$$\begin{gathered} \text{perplexity}=\prod_{t=1}^T\left(\frac{1}{P_{\mathrm{LM}}(\boldsymbol{x}^{(t+1)}| \boldsymbol{x}^{(t)},\ldots,\boldsymbol{x}^{(1)})}\right)^{1/T} \\ =\prod_{t=1}^T\left(\frac1{\hat{\boldsymbol{y}}_{\boldsymbol{x}_{t+1}}^{(t)}}\right)^{1/T}=\exp\left(\frac1T\sum_{t=1}^T-\log\hat{\boldsymbol{y}}_{\boldsymbol{x}_{t+1}}^{(t)}\right)=\exp(J(\theta)) \end{gathered}$$

这里详细说一下什么是困惑度PPL。

直观上理解，当我们给定一段非常标准的，高质量的，符合人类自然语言习惯的文档作为测试集时，模型生成这段文本的概率越高，就认为模型的困惑度越小，模型也就越好。

比如说测试文档只有一句话： 爱你就像爱生命。

那么拆分成token：

tokens_map = {
    '爱': 0,
    '你': 1,
    '就': 2,
    '像': 3,
    '生': 4,
    '命': 5,
    '。': 6,
}

一般情况下，使用GPT类模型生成上面这句话的时候，我们会拿到形状为 [句子长度, 词表长度] 的概率矩阵，假设分别为：

probs_modelA = [
    [0.16, 0.16, 0.16, 0.16, 0.16, 0.16, 0.04], 
    [0.05, 0.30, 0.05, 0.40, 0.05, 0.10, 0.05], 
    [0.30, 0.05, 0.30, 0.20, 0.05, 0.05, 0.05], 
    [0.20, 0.10, 0.05, 0.50, 0.05, 0.05, 0.05], 
    [0.30, 0.30, 0.05, 0.05, 0.10, 0.15, 0.05], 
    [0.05, 0.05, 0.05, 0.15, 0.35, 0.30, 0.05], 
    [0.05, 0.05, 0.05, 0.15, 0.05, 0.60, 0.05]，
    [0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.70]
]

probs_modelB = [
    [0.16, 0.16, 0.16, 0.16, 0.16, 0.16, 0.04], 
    [0.05, 0.50, 0.05, 0.20, 0.05, 0.10, 0.05], 
    [0.30, 0.05, 0.40, 0.10, 0.05, 0.05, 0.05], 
    [0.10, 0.10, 0.05, 0.60, 0.05, 0.05, 0.05], 
    [0.40, 0.30, 0.05, 0.05, 0.10, 0.05, 0.05], 
    [0.05, 0.05, 0.05, 0.15, 0.40, 0.25, 0.05], 
    [0.05, 0.05, 0.05, 0.15, 0.05, 0.60, 0.05]，
    [0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.70]
]

分别计算两个模型生成这段话的概率：

对模型A，从上到下取每一行的最大值，即可得到概率序列 [0.16, 0.30, 0.30, 0.50, 0.30, 0.35, 0.60, 0.70] 。准确理解如下：

P(“爱”)=0.16，第一行第一列
P(“你”|“爱”)=0.30 第二行第二列
...

同理，得到模型B的概率序列[0.16, 0.50, 0.40, 0.60, 0.40, 0.40, 0.60, 0.70]

现在来计算两个模型生成这句话的概率：

$$log_2PA=log_2(0.16*0.30*0.30*0.50*0.30*0.35*0.60*0.70)=-11.62$$

$$log_2PB=log_2(0.16*0.50*0.40*0.60*0.40*0.40*0.60*0.70)=-9.59$$

那么根据计算结果，就是B模型生成这句话的概率更高。

这个结果我们可以理解为模型B可能是一个作家，相对更容易写出这样的句子，模型A是一个小学生，很难写出这样的句子。所以在这个测试集下B比A好。

那么困惑度PPL的定义：

$$\begin{aligned}&perplexity(W)=P(w_1,w_2,w_3,w_4,\ldots\ldots,w_n)^{-\frac1N}=\sqrt[N]{\frac1{P(w_1,w_2,w_3,w_4,\ldots\ldots,w_n)}}\\&=\sqrt[N]{\prod_{i=1}^n\frac1{P(w_i|w_1,w_2,\ldots w_{i-1})}}\end{aligned}$$

由上面的公式可以看出，生成句子的概率越高，模型越好，困惑度也就越小。

根据上面的概率计算结果，两个模型的困惑度分别为：

$$perplexity_{A}(W)=\sqrt[N]{\frac1{0.16*0.30*0.30*0.50*0.30*0.35*0.60*0.70}}=2.74\\perplexity_{B}(W)=\sqrt[N]{\frac1{0.16*0.50*0.40*0.60*0.40*0.40*0.60*0.70}}=2.30$$

计算结果和之前保持一致，B模型的困惑度小于A模型。

根据上面的例子，我们其实看出来了，困惑度的计算其实依赖于语言模型输出token的概率分布，因此在比较语言模型时，其实是在比较哪个分布更符合测试集的真实概率分布。

具体比较的概率分布可以用下面的式子来表示：

$$P(x|context) $$

即给定前文，下一个token的概率。

我们假设测试集的真实概率分布为P，模型A输出的概率分布为MA，模型B输出的概率分布为MB.

来衡量两个分布的差异用KL散度。

对P和MA，（当然MB也一样），KL散度的定义为：

$$D_{KL}(P||MA)=\sum_{i=1}^NP(x_i)[logP(x_i)-logMA(x_i)]$$

KL散度只有在MA和P之间的分布一致时，才会为0

那么KL散度和交叉熵什么关系呢？

我们可以看一下信息熵P的表示：

$$H(P)=-\sum_{i=1}^NP(x_i)logP(x_i)$$

而交叉熵cross entropy的表示为：（以P分布和A模型分布为例）：

$$H(P,MA)=-\sum_{i=1}^NP(x_i)\log MA(x_i)$$

而KL散度的表示（还是以P和A分布为例）：

$$D_{KL}(P\parallel MA)=\sum_{i=1}^NP(x_i)\log\frac{P(x_i)}{MA(x_i)}$$

那么推导一下：

  1. 把KL散度展开：
    $$D_{KL}(P\parallel MA)=\sum_{i=1}^NP(x_i)\left[\log P(x_i)-\log MA(x_i)\right]$$

  2. 将这个式子展开为两个求和：
    $$D_{KL}(P\parallel MA)=\sum_{i=1}^NP(x_i)\log P(x_i)-\sum_{i=1}^NP(x_i)\log MA(x_i)$$

  3. 注意到第一个求和项是熵的定义，因此我们可以将其替换为：
    $$D_{KL}(P\parallel MA)=H(P)-\sum_{i=1}^NP(x_i)\log MA(x_i)$$

  4. 注意到第二项也是散度的定义

$$D_{KL}(P\parallel MA)=H(P)-(-H(P,MA))$$

  1. 那么结论就是：

$$H(P,MA)=H(P)+D_{KL}(P\parallel MA)$$

交叉熵=原始分布的熵+两个分布之间的KL散度。这意味着，交叉熵不仅包含了原始分布的不确定性，还包含了两个分布之间的差异。KL散度越小，交叉熵越小，意味着分布越接近。所以，对测试集困惑度越小的模型，交叉熵也会越小。

什么是语言中的信息熵

我们用H(P)表示测试集的信息熵，但真实的含义是用测试集来估算语言自身的信息熵，因为在实践中如果我们想要计算一门语言L的信息熵，我们需要找出所有长度为n的序列来计算熵，像下面这样：
$$\begin{aligned}&H(P)=-\frac1n\lim_{n\to\infty}\sum_{w_1^n\infty L}P(w_1,w_2,w_3,w_4,\ldots\ldots,w_n)logP(w_1,w_2,w_3,w_4,\ldots\\&\ldots,w_n)\end{aligned}$$

然而我们不可能找出所有长度为n的序列.

如果一个语言是稳定的且是可遍历的，那么该语言分布的信息熵率可以写作：
$$H(P)=-\frac{1}{n}\lim_{n\to\infty}P(w_1,w_2,…,w_n)logP(w_{1},w_{2},w_{3},w_{4},\ldots\ldots,w_{n})$$

这里简化的公式去除了对所有序列的要求，唯一的要求是$n\to\infty $.直觉上来说，这里蕴含的意思是无限长的文本包含了该语言所有的序列。

这意味着，只要我们找到足够长的文本，其实就是我们的测试集，就可以用下式来估算该语言的真实熵：

$$H(P)=-\frac{1}{n}P(w_1,w_2,…,w_n)logP(w_1,w_2,w_3,w_4,\dots\dots,w_n)$$

交叉熵也类似，就不展开了。

那么我们就可以得到终极目标：交叉熵和困惑度的关系：

打断施法（bushi

我们需要注意，熵和交叉熵中，都有$P(x_i)$这一项，表示真实分布的情况，但通常的（在nlp任务中）的公式表示中没有这一项，原因是 这一项通常是表示目标分布（也就是真实标签）的概率，通常是一个one-hot向量，也就是0-1表示。所以表示的时候省略这一项，也就是只保留非0项，是合理的。

当然，这里又得插一句：这是不用label smoothing的情况，目标分布只是普通的one-hot向量表示的情况。至于正则化技术label smoothing，这个后面单独出一个去了解透彻，记下啦~

所以，对于单个token的交叉熵的表示，就可以是：

$$J_t=-\sum y_tlog(p_t)$$

对于整个句子的平均token交叉熵表示：

$$J=\frac{1}{N}\sum_{n=1}^{N}J_{n}=-\frac{1}{N}\sum_{n=1}^{N}log(p_{t})\\=log((p_{t1}*p_{t2}*\ldots*p_{tN})^{-\frac{1}{N}})$$

句子概率的表示为：

$$P(S)=P(W_1)P(W_2|W_1)\ldots P(W_n|W_1,W_2,\ldots,W_{n-1})$$

困惑度PPL的表示为，将这个连乘形式代入困惑度公式中：

$$\text{Perplexity}(W)=(P(w_1)P(w_2\mid w_1)P(w_3\mid w_1,w_2)\ldots P(w_n\mid w_1,w_2,\ldots,w_{n-1}))^{-\frac1n}$$

可以将乘积展开为每个条件概率的幂：

$$\text{Perplexity}(W)=\left(\prod_{i=1}^nP(w_i\mid w_1,w_2,\ldots,w_{i-1})\right)^{-\frac1n}$$

因为乘法的幂等于每个项的幂的乘积，所以：

$$\text{Perplexity}(W)=\prod_{i=1}^nP(w_i\mid w_1,w_2,\ldots,w_{i-1})^{-\frac1n}$$

再用exp和log的带入：

$$\text{Perplexity}(W)=\exp\left(-\frac1n\sum_{i=1}^n\log P(w_i\mid w_1,w_2,\ldots,w_{i-1})\right)$$

这里注意，括号里面的部分就是交叉熵损失函数的表示。

舒服了哈哈哈哈

那么就得出了PPL和交叉熵ce的关系：

$$\text{Perplexity}(W)=\exp(H(P,MA))$$

也就是： 困惑度是交叉熵的指数形式。

晚上吃完饭再回来继续搞RNN与LSTM（待续hhh

开始了又

2024-08-19

到这里我觉得可以总结一下RNN家族的特点：
1. 接受任意长度的输入序列
2. 可以每一步共享参数
3. 每一步可以选择性输出

但RNN得架构也不是完美的，存在诸多问题：

梯度消失

求解变量的梯度进而进行反向传播更新，是正常的一步操作。因为求导遵循链式法则，而势必会有多个因子的相乘，只要其中的一项或者几项比较小，那么本次梯度的结果就会很小，那么更新的幅度就会很小，次数多了就会几乎不更新了。

举一个比较实际的例子，这里我们假设激活函数不是非线性的，只是恒等函数x，那么就会有以下的求解梯度情况：

26.png

27.png

所以说为什么这个梯度消失是一大问题呢？

原因就是这样的话，只能传递当前节点比较近的节点的信息，而远距离的节点信息就会丢失的。

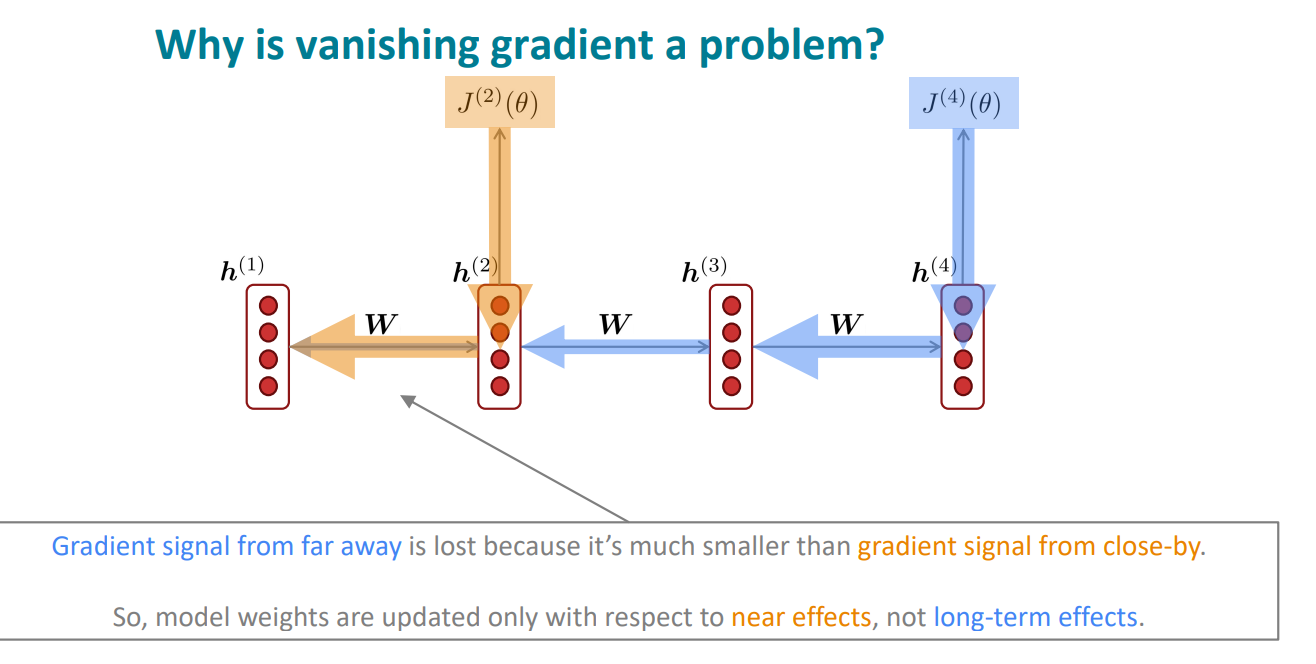
28.png

我们再从数学公式的角度推导理解一下：

RNN的输入、输出及hidden state的关系有如下的公式表示：

$$\begin{aligned}&h_{t}=f(Wh_{t-1}+W_xx_t)\\&\hat{y}_{t}=softmax(Uh_t)\end{aligned}$$

并且其损失函数为：
$$\begin{aligned}&J=\frac{1}{T}\sum_{t=1}^{T}J_{t}\\&J_{t}=-\sum_{j=1}^{|V|}y_{t,j}log\hat{y}_{t,j}\end{aligned}$$

所以损失函数相对于W的梯度为：

$$\begin{aligned} &\frac{\partial J}{\partial W} =\sum_{t=1}^{T}\frac{\partial J_{t}}{\partial W} \\ &\frac{\partial J_{t}}{\partial W} =\sum_{k=1}^{t}\frac{\partial J_{t}}{\partial y_{t}} \frac{\partial y_{t}}{\partial h_{t}} \frac{\partial h_{t}}{\partial h_{k}} \frac{\partial h_{k}}{\partial W} \\ &\text{其中 }\frac{\partial h_{t}}{\partial h_{k}}=\prod_{j=k+1}^{t}\frac{\partial h_{j}}{\partial h_{j-1}}=\prod_{j=k+1}^{t}W^{t-k}\times diag[f^{\prime}(h_{j-1})] \end{aligned}$$

假设矩阵W的最大的本征值也小于1，则t-k越大的时候，表示其相距越远，其梯度会呈指数级衰减，导致我们无法分辨t时刻与k时刻究竟是数据本身毫无关联还是由于梯度消失而导致我们无法捕捉到这一关联。这就导致了我们只能学习到近程的关系而不能学习到远程的关系，会影响很多语言处理问题的准确度。

梯度爆炸

这也很糟糕，会让参数更新的非常突兀，刚才还在hill，马上到lowa。

而且最糟糕的情况，大概就是会溢出，得到inf或者nan等结果，就直接终止训练了。

29.png

但梯度爆炸比较好解决，那就别让他爆炸呗。

梯度裁剪 gradient clipping：

设定一个阈值，如果梯度超过了这个阈值，那么就缩小这个梯度，然后再执行SGD进行反向传播。

30.png

有梯度裁剪和没有梯度裁剪的训练对比如下：

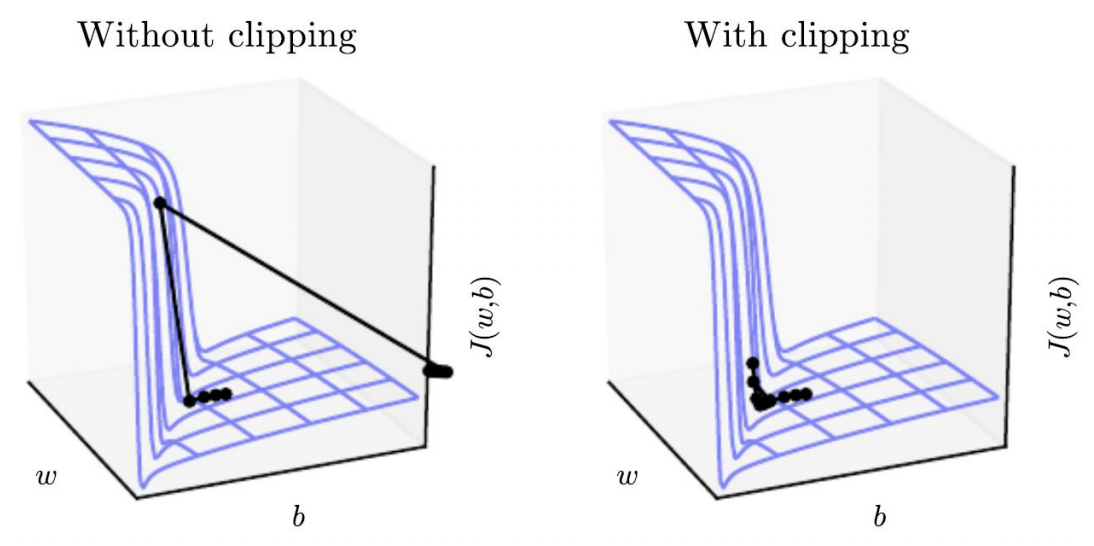
31.png

可见左图中由于没有进行clipping，步进长度过大，导致损失函数更新到一个不理想的区域，而右图中进行clipping后每次步进减小，能更有效的达到极值点区域。

但梯度爆炸不是最重要的问题，因为这个好解决，真正的问题还是梯度消失 gradient vanishing

那么有什么好的优化的思路嘛？

我的直觉就是，因为RNN去找前面节点的信息，就只能去一个个找，因为隐藏层是按照时间步长的串行，那如果这些信息和长度能单独的存储单元存呢？

好吧这就是LSTM的初衷。

如果能进一步建立词与词更加直接的联系就好了。

好吧，这就是attention和残差网络。

我们下面就开始吧！RNN就到这里先~

参考

https://zhuanlan.zhihu.com/p/651410752
https://zhuanlan.zhihu.com/p/63397627
https://web.stanford.edu/class/cs224n/slides/cs224n-spr2024-lecture05-rnnlm.pdf
https://www.bilibili.com/video/BV18Y411p79k/?p=6&spm_id_from=pageDriver&vd_source=de334f24ee86583df2785811808ca76b

0 评论