说实话进阶课开局来两小时的概念叙述属实感觉硬核，，
咱对那些概念不是很了解，对着概念去理解而学习，也总感觉不自然
干脆不听讲了，找看博客，等有一定理解了再听y总讲课会好一点，

首先我得去知道网络流是个什么东西，，，，

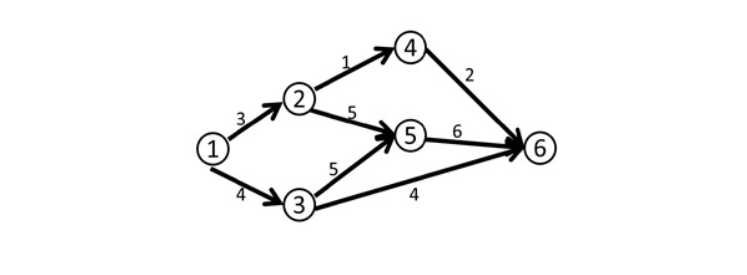
如图 网络流大概长这个样子

数字代表边的权重

有的博客把这些边比作水管 那么这些权值就是这个水管的最大流量值 诶，注意了，这里是允许的最大流量值，，

这不就是堆水管吗，好说

而且这些水管是有性质的呢，，，，

首先图上的边 上的数字代表的是 这个管内最大的流量

之所以称它为最大 是因为 边上的数字可以比它小，，，至于小到多少，，看自己分配

对于图上的每一个点，出边的权值和 要等于 入边的权值和 这里的边的权值都是自己之后规定的 和图中边上的数字不一样，，

诶，我对网络流有了初步的认知，特定的限制条件 ，一组有特殊关系的边， 自己可以分配每条边的流量

首先就是这些边与边直接都是你死我活的关系，，

诶，如果从源点到汇点有条通路
那么这条路上的边就都要拼个你死我活，，，好，，有争斗了，那么就会有损伤，甚至这条路上有的边太弱小了当场去世

这部分等我有空了再写### 鸽鸽鸽

这个入门介绍太长了，写起来没意思，我们直接上大招，

对于建图中 f数组的理解，正向边就是最大容量没什么好说的，那反向边呢？？为什么正向边减少的同时反向边要增加

$\color{#32CD32}{反向边是什么？}$
我们先来看两种情况

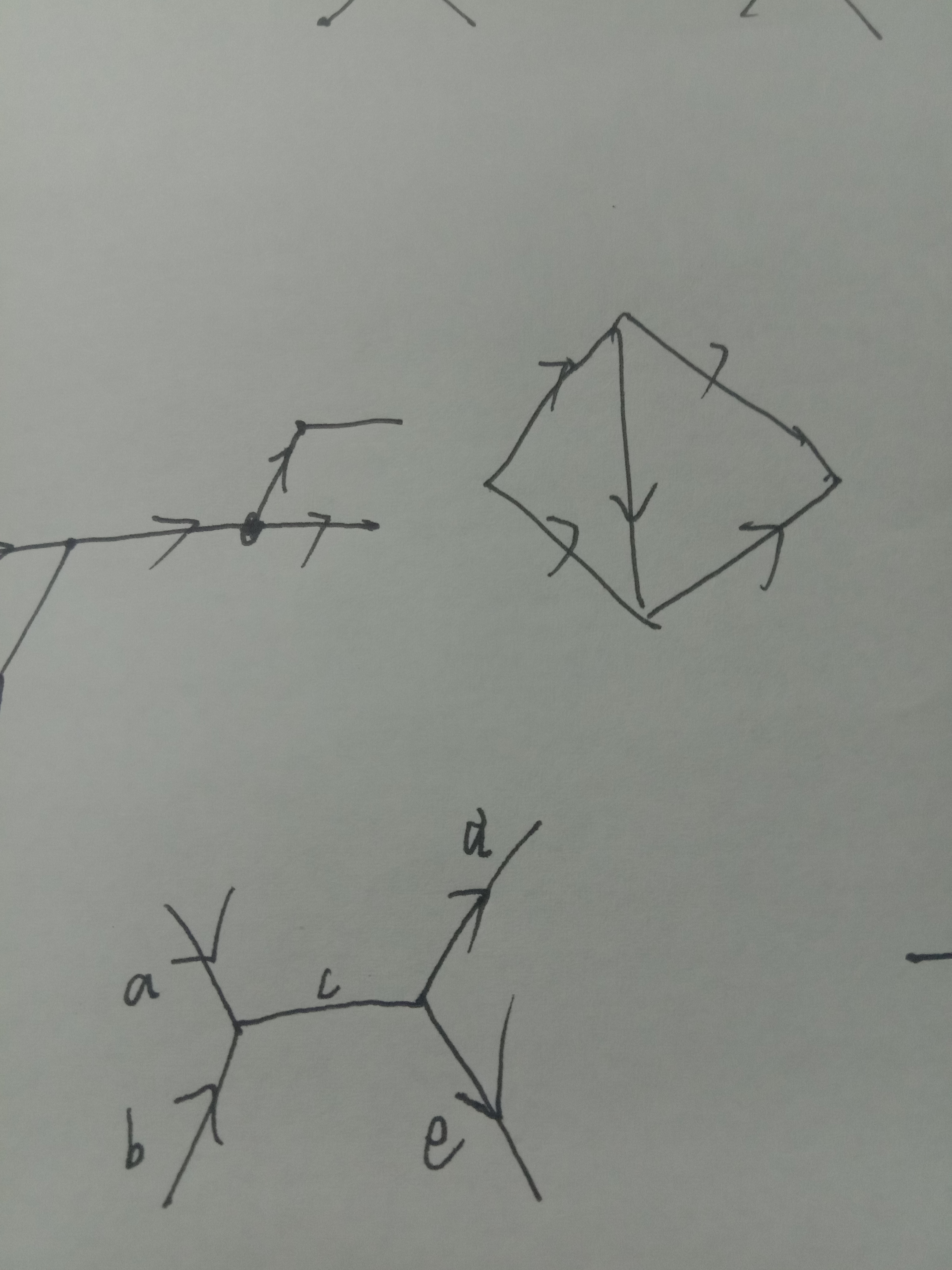
我发现这个图片传到acwing上会有点爆炸

c这条边 在a->c->d 和b ->c ->d 用了两次，， 是公共边

所以这种情况不存在 由于遍历的顺序不同会导致结果不同，， 因为c的流量不管给谁都发挥同样大的作用，

再来看另一种情况

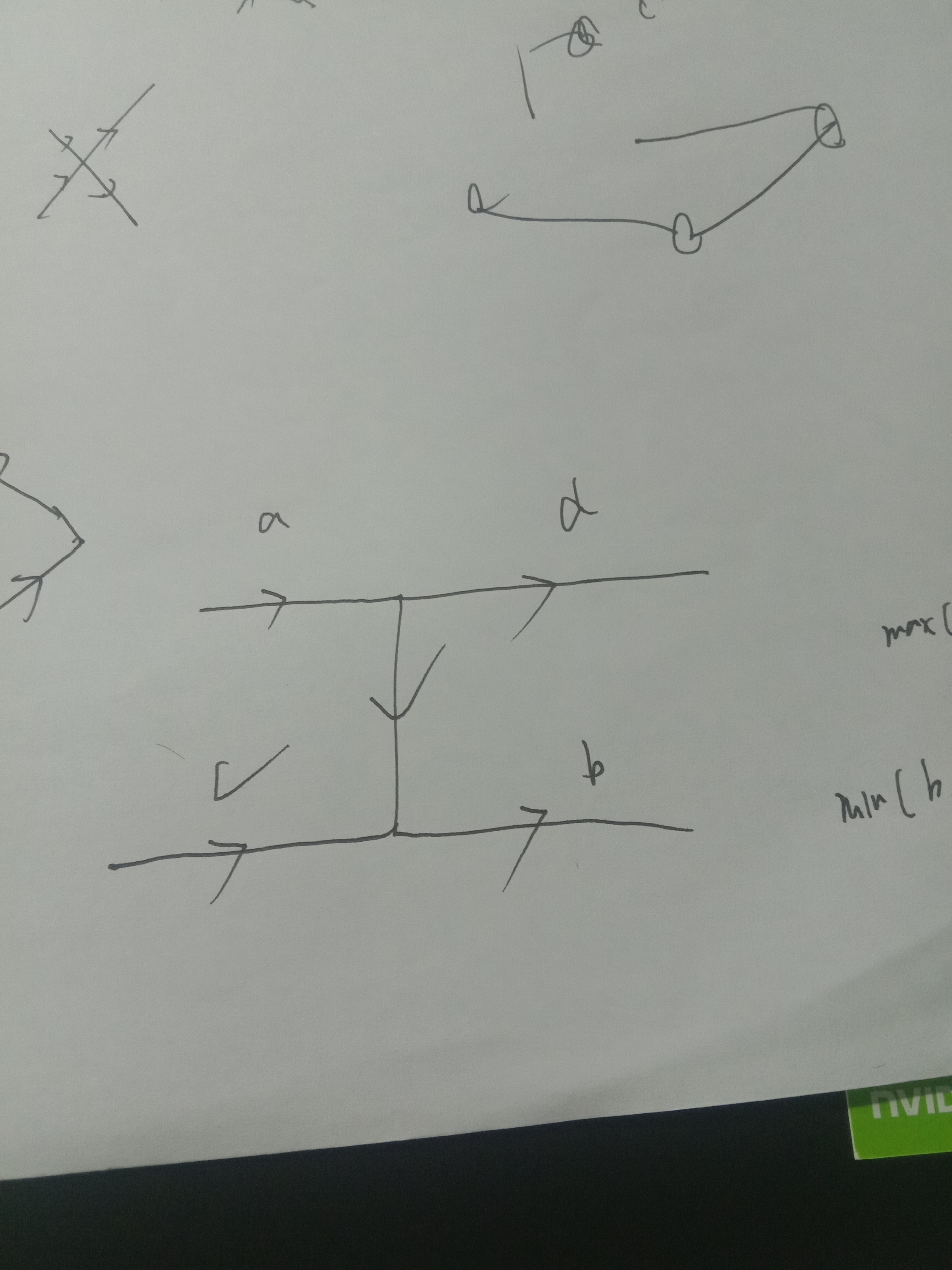
这个图片再次爆炸，，
这里就不一样了，，把中间的那条边叫做e

这里有 a->d c->b

和 a->e ->d

**结论就是 如果aed这条边的 e 有了给S 到 T的贡献 那么 这个贡献会小于等于 a和b的最小值
也就是说 单独把这个贡献 的数值拿出来跟a或者d或者e打一架 a 或d 都还能活着，，
那么 你让这个贡献去和d 或c 打一架 肯定能剩一个ad这条边 或 cb这条边的贡献

然后你再看 e这条边 先被a 穿过后被 b穿过，， e的反向边 先被c穿过 后被 d穿过
如果说e的正向边 被用了的话，，，之后如果再用到了 e的反向边 （能用到说明有通路）
也就是说 横跨在e 至少有两条路，， ad 和cb

你增加了一个反向边，，不论搜索顺序，ad和cb 与 aeb 的对汇点的贡献大的那一方都会被考虑到

这样就避免了，先搜到aed然后 a或b当场去世 之后 ad不通或者 cb不通 从而有可能减少给汇点的贡献的情况，

第一次用到e 是a和b 损失了一些权值
第二次用到e的反向 就是 c和d 损失了一些权值
相当于 ad 这条边 然后 再是 cb这条边

贼nb的反悔机制，而且仔细想想 第二次 的ced 给c和d损失的值不会超过 走ad 和 cb 下 c 和d 损失的值，
$\color{#32CD32}{pefect}$

至此，我们理解了反向边的意义

后面还会更新y总说的 有源汇上下界最大最小流的 新建的S T图上 不能直接跑小s 和小t 的最大流的问题
睡觉睡觉，，，，