树状数组：

树状数组是一个查询和修改复杂度都为$log(n)$的数据结构。
主要用于数组的单点修改和区间求和.
另外一个拥有类似功能的是线段树.

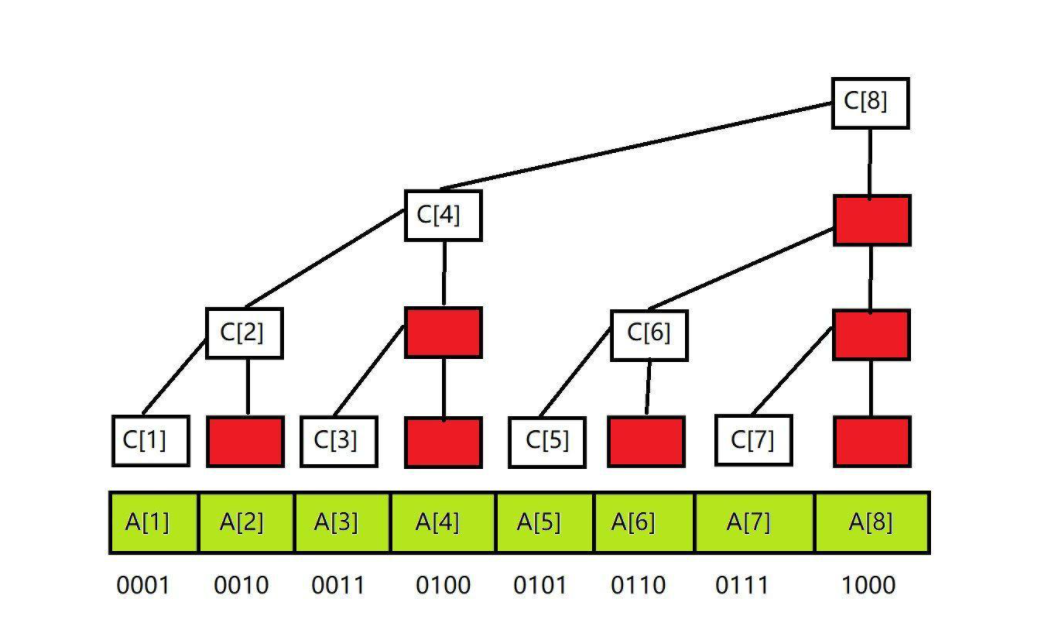
$1=(001) C[1]=A[1]$; $lowbit$结果为1，故只有一项
$6=(110) C[6]=A[6]+A[5]$;
由上图可知：C[i]有几项取决于$lowbit$结果

$lowbit(x)$= x & -x 操作返回在二进制表示下最低位1及后面的0构成的数值

$lowbit(44)$ = $lowbit(101100)$ = $(100)$(二进制)= $4$

//注意 x 直接以十进制输入

int lowbit(int x)
{
    return x&(-x);
}

单点修改 + 区间查询

单点更新

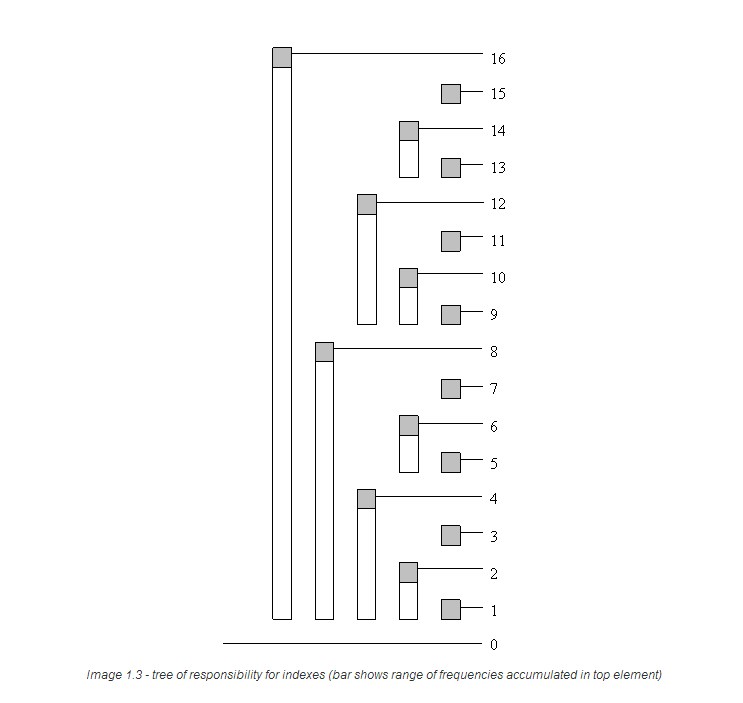
//读入一个点，就修改相关区间的数值
void update(int i,int val){
    while(i<=n){
        C[i]+=val;
        i+=lowbit(i);  //由叶子节点向上更新C数组 
    }
}//更新(从小到大)是查询(从大到小)的逆过程 
  //得到每个C[i]的值

求前缀和（单点更新的逆操作）

int summ(int i){//求区间[1,i]所有元素的和 
    int sum=0;
    while(i>0){
        ret+=C[i];
        i-=lowbit(i);
    }
    return sum;
} 
/*若 i 是7，sum+=C[7];
  7-1=6,sum+=C[6]
  6-2=4,sum+=C[4]
  4-4=0,break;
*/

区间查询

先构造好$C[i]$数组 （undate函数）
$summ(R)-summ(l-1)$; (summ函数)

【模板题目： HDU-1166 敌兵布阵 】

/*1
10
1 2 3 4 5 6 7 8 9 10
Query 1 3
Add 3 6
Query 2 7
Sub 10 2
Add 6 3
Query 3 10
End 
*/

#include<bits/stdc++.h>
using namespace std;
int t,n,a,k;
const int N=500005;
int C[N];

int lowbit(int x){
    return x&(-x);
}
void update(int a,int b){
    while(a<=n){
        C[a]+=b;
        a+=lowbit(a);
    }
}

int summ(int i){
    int sum=0;//在这里赋值为0 
    while(i>0){
        sum+=C[i];
        i-=lowbit(i);
    }
    return sum;
}
int main(){
    cin >> t;
    while(t--){
        k++;
        cin >> n;
        memset(C,0,sizeof(C));
        for(int i=1;i<=n;i++){//记得从 1 开始
            cin>>a;
            update(i,a); 
        }
        cout << "Case " << k << ":" <<endl;
        int x,y;
        string s;
        while(cin >> s){
            cin>>x>>y;
            if(s=="END") break;
            else if(s=="Add") update(x,y);
            else if(s=="Sub") update(x,-y);
            else if(s=="Query") cout<<summ(y)-summ(x-1)<<endl;

        }
    }

    return 0;
}

【应用：求逆序对 】

/*
求交换的次数
单点修改，查询区间(a+1,n)有多少个 1，区间查询：summ(n)-sum(a);
4 
4 2 3 1

*/
#include <bits/stdc++.h>
using namespace std;
int t,n,k;
const int N=500005;
int sum[N];

int lowbit(int x){
    return x&(-x);
}

void update(int x,int y){
    while(x <= n){
        sum[x]+=y;
        x+=lowbit(x);
    }
}

int summ(int i){
    int ans=0;
    while(i>0){
        ans+=sum[i];
        i-=lowbit(i);
    }
    return ans;
}
int main(){
    int a;
    while(cin >> n){
        int cnt=0;
        for(int i=1;i<=n;i++){//从 1 开始
            cin>>a;
            update(a,1);//注意这里数值于=与上一题的差别
            cnt+=summ(n)-summ(a);//每一轮有多少逆序对
    }   cout<<cnt<<endl;
    }
    return 0;
}

区间修改(看作左右两个端点修改)+单点查询

【模板题目：Color the ball(前缀和) 】

/*
涂气球（求每个气球被涂的次数）
输入:
3
1 1
2 2
3 3
3
1 1
1 2
1 3
0
输出：
1 1 1
3 2 1
*/
#include <bits/stdc++.h>
using namespace std;
int t,n,k;
const int N=500005;
int sum[N];
int s[N];

int lowbit(int x){
    return x&(-x);
}

void update(int x,int y){
    while(x <= n){
        sum[x]+=y;//差分数组
        x+=lowbit(x);
    }
}

int summ(int i){
    int ans=0;
    while(i>0){
        ans+=sum[i];
        i-=lowbit(i);
    }
    return ans;
}
int main(){
    while(scanf("%d",&n)!=EOF){

        memset(sum,0,sizeof(sum));//原本都是0 不用表示差分数组
        for(int i=1;i<=n;i++){//
            int a,b;
            cin >> a>> b;//区间修改
            update(a,1);
            update(b+1,-1);
        }
        printf("%d",summ(1));  
        for(int i=2;i<=n;i++)  
        {  
            printf(" %d",summ(i));  
        }  
        printf("\n");  
    }  
    return 0;  
}  

区间修改 + 区间查询

区间修改

void update(int x,int y){
    for(int i=x; i <= n ;i+=lowbit(i)){//要用for,因为 x 的值sum1，sum2会用到
        sum1[i] += x;
        sum2[i] += x*p;
    }
}
void summ(int l ,int r, int x){
    update(l,x);
    update(r+1,-x);
}

区间查询

int ask(int x){
    int ans=0;
    for(int i = p;i ;i-=lowbit(i)){
        ans += (x+1) * sum1[i]-sum2[i];
    }
    return ans;
}
int range_ask(int l,int r){
    return ask(r) - ask(l-1);
}

参考资料
https://blog.csdn.net/bestsort/article/details/80796531