布隆过滤器(一)
背景
在平常生活中,包括在设计计算机软件时,我们经常要判断一个元素是否在一个集合中。比如在 FBI,一个嫌疑人的名字是否已经在嫌疑名单上;在网络爬虫里,一个网址是否被访问过等等。
最直接的方法就是将集合中全部的元素存在计算机中,遇到一个新元素时,将它和集合中的元素直接比较即可。一般来讲,计算机中的集合是用哈希表(hash table)来存储的。它的好处是快速准确,缺点是浪费存储空间。那有没有 更优化的数据结构呢?
简介
布隆过滤器(Bloom Filter)是1970年由布隆提出的。它实际上是由一个很长的bit数组和一系列哈希函数组成的。布隆过滤器可以用于检索一个元素是否在一个集合中。
原理
数组的每个元素都只占1bit空间,并且每个元素只能为0或1。
布隆过滤器还拥有k个哈希函数,当一个元素加入布隆过滤器时,会使用k个哈希函数对其进行k次计算,得到k个哈希值,并且根据得到的哈希值,在维数组中把对应下标的值置位1。
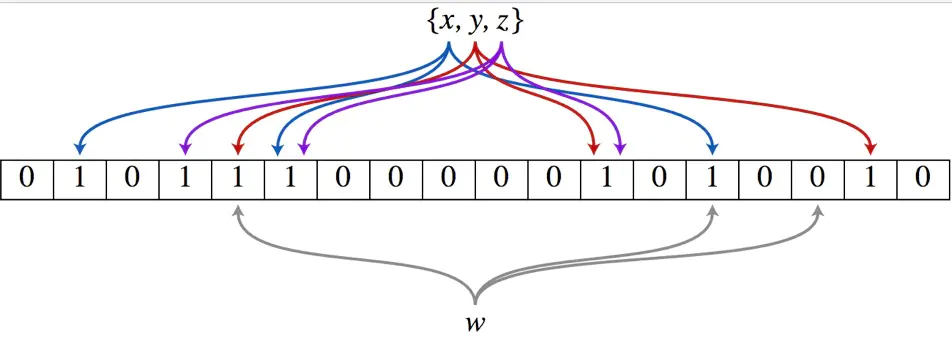
判断某个数是否在布隆过滤器中,就对该元素进行k次哈希计算,得到的值在位数组中判断每个元素是否都为1,如果每个元素都为1,就说明这个值在布隆过滤器中。
布隆过滤器的工作过程
- 初始化

- 插入geeks单词
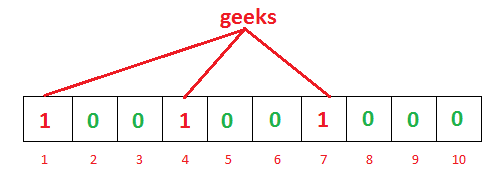
- 插入nerd
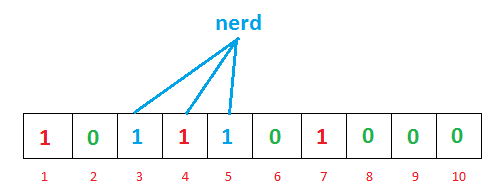
- 查询cat
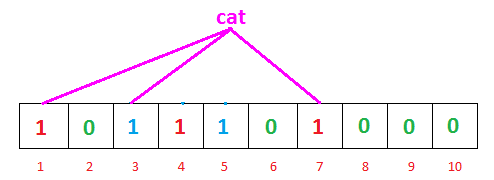
cat这个单词并不存在,但是此时1,3,7号位均为1,表示查询到了cat这个单词。此时需要去后台数查询。这个情况就是出现了误差。
布隆过滤器的误差率是指由于hash冲突,导致原本不再布隆过滤器中的数据,查询时显示在里面。
False positives 概率 (误差率)
推导
假设 Hash 函数以等概率条件选择并设置 Bit数组中的某一位,m 是该位数组的大小,k 是 Hash 函数的个数,n插入bit数组中的元素的个数。
数组中某一特定的位在进行元素插入时的 Hash 操作中没有被置位1的概率是:
$1-\frac{1}{m}$
那么在所有 k 次 Hash 操作后该位都没有被置 “1” 的概率是:
$\left(1-\frac{1}{m}\right)^{k}.$
如果我们插入了 n 个元素,那么某一位仍然为 “0” 的概率是:
$\left(1-\frac{1}{m}\right)^{kn}$
因而该位为 “1”的概率是:
$1-\left(1-\frac{1}{m}\right)^{kn}.$
现在检测某一元素是否在该集合中。标明某个元素是否在集合中所需的 k 个位置都按照如上的方法设置为 “1”,但是该方法可能会使算法错误的认为某一原本不在集合中的元素却被检测为在该集合中(False Positives),该概率由以下公式确定:
$\left(1-\left[1-\frac{1}{m}\right]^{kn}\right)^{k}$
m 是该位数组的大小,n插入bit数组中的元素的个数。在实际应用中m和n都非常大(我们希望在任何情况下,确定一个k值,使误报率最小)。所以我们需要一个$m\rightarrow+\infty $ 时 k 的函数(n视为一个常数,因为与n无关)
以下为推导过程:
${\because 当x\rightarrow0,(1+x)^{\frac{1}{x}}\rightarrow e} $ ①
又有 $(1-[1-\frac{1}{m}]^{kn})^{k}=(1-[1-\frac{1}{m}]^{-m\times\frac{-kn}{m}})^{k} \\$ ②
$\because m\rightarrow+\infty $ $\therefore-\frac{1}{m}\rightarrow0$
此时可以将$\frac{-1}{m}$当成公式①中的X,那么原公式可推导出
$(1-[1-\frac{1}{m}]^{kn})^{k}\rightarrow(1-e^{-\frac{n}{m}k})^{k}$
不难看出,随着m (位数组大小)的增加,假阳性(False Positives)的概率会下降,同时随着插入元素个数 n 的增加,False Positives的概率又会上升。
对于给定的m,n,如何选择Hash函数个数 k ?
根据我们推导出的误判率函数 $$f(k)=\left(1-e^{-\frac{nk}{m}}\right)^k$$。我们希望误判率最小,问题变为求 $f(k)$ 的最小值
以下为推导过程:
设:$$\mathbf{b}=\mathrm{e}^{\frac{n}{m}}$$,则函数变为$$f(k)=(1-b^{-k})^{k}$$
两边取对数:$$lnf(k)=k\cdot ln(1-b^{-k})$$
$$\begin{aligned}\frac{1}{f(k)}\cdot f^{\prime}(k)&=ln(1-b^{-k})+k\cdot\frac{1}{1-b^{-k}}\cdot(-b^{-k})\cdot lnb\cdot(-1)\\&=ln(1-b^{-k})+k\cdot\frac{b^{-k}\cdot lnb}{1-b^{-k}}\end{aligned}$$
下面求最值:
$$ln(1-b^{-k})+k\cdot\frac{b^{-k}\cdot lnb}{1-b^{-k}}=0$$
$$(1-b^{-k})\cdot ln(1-b^{-k})=-k\cdot b^{-k}\cdot lnb$$
$$(1-b^{-k})\cdot ln(1-b^{-k})=b^{-k}\cdot lnb^{-k}$$
$$1-b^{-k}=b^{-k}$$
$$b^{-k}=\frac{1}{2}$$
$$\mathrm{e}^{\frac{kn}{m}}=\frac{1}{2}$$
$\frac{kn}{m}=ln2$
则误判率最低时,得出k值:
$$k=ln2\cdot\frac{m}{n}\approx0.7\frac mn$$
把k代入误判率公式,得出:
$$P(error)=\left(1-\frac{1}{2}\right)^{k}=2^{-k}=2^{-in2\cdot\frac{m}{n}}$$
而对于给定的False Positives概率 p,如何选择最优的位数组大小 m 呢?
把k代入误判率公式,得出m值:
$$P=2^{-\mathrm{in2}\:\frac{m}{n}}\Longrightarrow\mathrm{lnp}=\mathrm{ln2}\cdot(-\mathrm{ln2})\cdot\frac{\mathrm{m}}{\mathrm{n}}\Longrightarrow\mathrm{m}=-\frac{n\cdot lnp}{(ln2)^{2}}$$
Hash函数选定
上文提及误差率主要是由于hash冲突导致的,所以选定一个好的hash函数至关重要。本文囊括了常见的hash函数,并从时间和冲突率统计各类hash函数测试结果
- 测试数据
- 随机字符串:约1000000
- 模拟app账号:2~28个字符,约45000
- 视频素材主键:1~9个字符的整型,约40000
- 测试结果
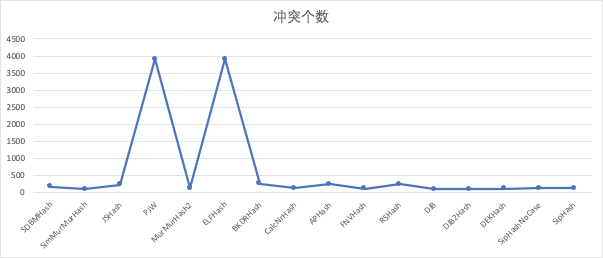
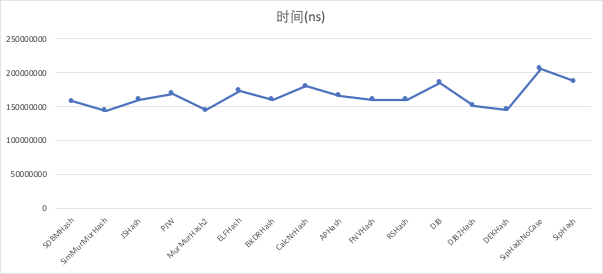
- 随机字符
| 哈希函数 | 时间(ns) | 冲突个数 | 总个数 |
|---|---|---|---|
| SDBMHash | 158062897 | 180 | 1000000 |
| SimMurMurHash | 144356292 | 108 | 1000000 |
| JSHash | 160829523 | 230 | 1000000 |
| PJW | 169142421 | 3901 | 1000000 |
| MurMurHash2 | 144678973 | 129 | 1000000 |
| ELFHash | 173966075 | 3901 | 1000000 |
| BKDRHash | 160517055 | 258 | 1000000 |
| CalcNrHash | 180425843 | 124 | 1000000 |
| APHash | 166644369 | 245 | 1000000 |
| BPHash | 144647091 | 920005 | 1000000 |
| FNVHash | 160584860 | 109 | 1000000 |
| RSHash | 160316468 | 240 | 1000000 |
| DJB | 185411123 | 97 | 1000000 |
| DJB2Hash | 151799803 | 97 | 1000000 |
| DEKHash | 145856752 | 119 | 1000000 |
| SipHashNoCase | 205930199 | 126 | 1000000 |
| SipHash | 187972639 | 126 | 1000000 |
- 视频素材主键
哈希函数时间(ns)冲突个数总个数
| 哈希函数 | 时间(ns) | 冲突个数 | 总个数 |
|---|---|---|---|
| SDBMHash | 1527902 | 0 | 40000 |
| SimMurMurHash | 1346732 | 0 | 40000 |
| JSHash | 1575731 | 0 | 40000 |
| PJW | 1482411 | 38 | 40000 |
| MurMurHash2 | 1396543 | 0 | 40000 |
| ELFHash | 1516443 | 38 | 40000 |
| BKDRHash | 1568576 | 0 | 40000 |
| CalcNrHash | 1900336 | 1 | 40000 |
| APHash | 1631107 | 0 | 40000 |
| BPHash | 1388693 | 9227 | 40000 |
| FNVHash | 1540261 | 1 | 40000 |
| RSHash | 1547968 | 0 | 40000 |
| DJB | 1969460 | 0 | 40000 |
| DJB2Hash | 1438242 | 1 | 40000 |
| DEKHash | 1359623 | 25 | 40000 |
| SipHashNoCase | 1727340 | 0 | 40000 |
| SipHash | 1480105 | 0 | 40000 |
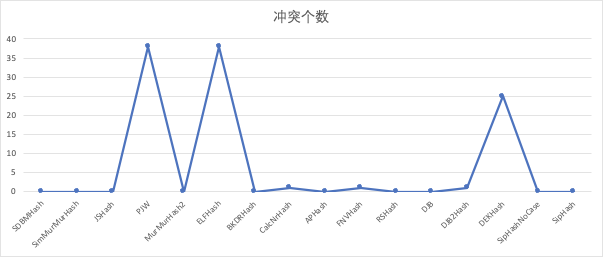
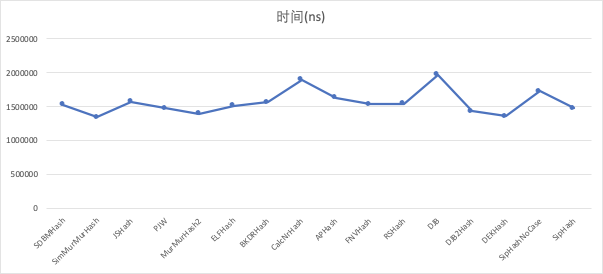
- 模拟app账号
哈希函数时间(ns)冲突个数总个数
| 哈希函数 | 时间(ns) | 冲突个数 | 总个数 |
|---|---|---|---|
| SDBMHash | 1900195 | 1 | 45402 |
| SimMurMurHash | 1949347 | 0 | 45402 |
| JSHash | 1904775 | 5 | 45402 |
| PJW | 2026217 | 170 | 45402 |
| MurMurHash2 | 1937634 | 0 | 45402 |
| ELFHash | 2047954 | 170 | 45402 |
| BKDRHash | 1905460 | 0 | 45402 |
| CalcNrHash | 2084442 | 0 | 45402 |
| APHash | 1961953 | 1 | 45402 |
| BPHash | 1893523 | 29253 | 45402 |
| FNVHash | 1888491 | 0 | 45402 |
| RSHash | 1929489 | 0 | 45402 |
| DJB | 2351529 | 30 | 45402 |
| DJB2Hash | 1867887 | 0 | 45402 |
| DEKHash | 1861001 | 17 | 45402 |
| SipHashNoCase | 2291959 | 29 | 45402 |
| SipHash | 2037517 | 0 | 45402 |
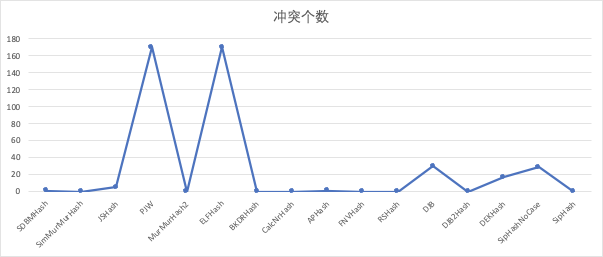
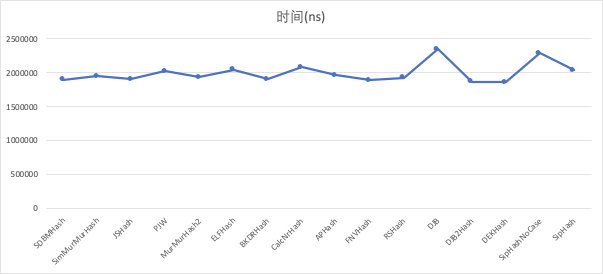
最终我们选择了MurMurHash2
布隆过滤器实战
接口设计
class BloomFilterPolicy final : public FilterPolicy {
public:
explicit BloomFilterPolicy(int bits_per_key) : bits_per_key_(bits_per_key) {
// We intentionally round down to reduce probing cost a little bit
k_ = static_cast<size_t>(bits_per_key * 0.69); // 0.69 =~ ln(2)
if (k_ < 1) k_ = 1;
if (k_ > 30) k_ = 30;
}
const char* Name() const override { return "BloomFilter2"; }
void CreateFilter(const std::string* keys, int n,
std::string* dst) override {
// Compute bloom filter size (in both bits and bytes)
size_t bits = n * bits_per_key_;
// For small n, we can see a very high false positive rate. Fix it
// by enforcing a minimum bloom filter length.
if (bits < 64) bits = 64;
size_t bytes = (bits + 7) / 8;
bits = bytes * 8;
const size_t init_size = dst->size();
dst->resize(init_size + bytes, 0);
dst->push_back(static_cast<char>(k_)); // Remember # of probes in filter
char* array = &(*dst)[init_size];
for (int i = 0; i < n; i++) {
//BloomFilter理论是通过多个hash计算来减少冲突,
//double-hashing的方式来达到同样的效果。
//double-hashing的理论如下:
//1、计算hash值;
//2、hash值的高15位,低17位对调
//3、按k_个数来存储当前hash值。
//3-1、计算存储位置;
//3-2、按bit存;
//3-3、累加hash值用于下次计算
// Use double-hashing to generate a sequence of hash values.
// See analysis in [Kirsch,Mitzenmacher 2006].
uint32_t h = hash_func_.MurMurHash2(keys[i].c_str(), keys[i].size());
const uint32_t delta = (h >> 17) | (h << 15); // Rotate right 17 bits
for (size_t j = 0; j < k_; j++) {
const uint32_t bitpos = h % bits;
array[bitpos / 8] |= (1 << (bitpos % 8));
h += delta;
}
}
}
bool KeyMayMatch(const std::string& key,
const std::string& bloom_filter) override {
const size_t len = bloom_filter.size();
if (len < 2) return false;
const char* array = bloom_filter.data();
const size_t bits = (len - 1) * 8;
// Use the encoded k so that we can read filters generated by
// bloom filters created using different parameters.
const size_t k = array[len - 1];
if (k > 30) {
// Reserved for potentially new encodings for short bloom filters.
// Consider it a match.
return true;
}
uint32_t h = hash_func_.MurMurHash2(key.c_str(), key.size());
const uint32_t delta = (h >> 17) | (h << 15); // Rotate right 17 bits
for (size_t j = 0; j < k; j++) {
const uint32_t bitpos = h % bits;
if ((array[bitpos / 8] & (1 << (bitpos % 8))) == 0) return false;
h += delta;
}
return true;
}
// Return a new filter policy that uses a bloom filter with approximately
// the specified number of bits per key. A good value for bits_per_key
// is 10, which yields a filter with ~ 1% false positive rate.
private:
size_t bits_per_key_;
size_t k_;
HashFunc hash_func_;
};
} // namespace hard_core
测试程序
class BloomTest final {
public:
BloomTest(uint32_t bit_per_key = 10)
: policy_(std::make_unique<BloomFilterPolicy>(bit_per_key)) {}
~BloomTest() {}
void Reset() {
keys_.clear();
filter_.clear();
}
void SetData(std::vector<std::string>&& keys) { keys_ = std::move(keys); }
void SetData(const std::vector<std::string>& keys) { keys_ = (keys); }
void Add(const std::string& s) { keys_.emplace_back(s); }
void Build() {
filter_.clear();
policy_->CreateFilter(&keys_[0], static_cast<int>(keys_.size()), &filter_);
keys_.clear();
}
size_t FilterSize() const { return filter_.size(); }
bool Matches(const std::string& s) {
if (!keys_.empty()) {
Build();
}
return policy_->KeyMayMatch(s, filter_);
}
double FalsePositiveRate(const std::vector<std::string>& data) {
double result = 0;
for (const auto& item : data) {
if (Matches(item)) {
result++;
}
}
return result / 10000.0;
}
double FalsePositiveRate(const std::string& data) {
double result = 0;
{
if (Matches(data)) {
result++;
}
}
return result / 10000.0;
}
private:
std::unique_ptr<FilterPolicy> policy_;
std::string filter_;
std::vector<std::string> keys_;
};
结果统计
| bit_per_key = 10 | ||||
|---|---|---|---|---|
| 数据集 | 原始数据空间占用 | bf空间占用 | 空间压缩比 | 误差率(/万) |
| 视频素材主键 | 710519 | 100001 | 0.8592564 | 0.0827 |
| 模拟app账号 | 363646 | 56754 | 0.84393064 | |
| bit_per_key = 15 | ||||
| 数据集 | 原始数据空间占用 | bf空间占用 | 空间压缩比 | 误差率(/万) |
| 视频素材主键 | 710519 | 150001 | 0.78888531 | 0.0074 |
| 模拟app账号 | 363646 | 85130 | 0.7658987 | |
| bit_per_key = 20 | ||||
| 数据集 | 原始数据空间占用 | bf空间占用 | 空间压缩比 | 误差率(/万) |
| 视频素材主键 | 710519 | 200001 | 0.71851421 | 0.0006 |
| 模拟app账号 | 363646 | 113506 | 0.68786677 |
布隆过滤器使用场景
- 黑名单校验
- 快速去重
- 爬虫URL校验
- leveldb/rocksdb快速判断数据是否已经block中,避免频繁访问磁盘
- 解决缓存穿透问题
重点讲解一下缓存穿透
缓存穿透
- 概念
缓存穿透是指查询一个数据库中不一定存在的数据;正常流程是依据key去查询value,数据查询先进行缓存查询,如果key不存在或者key已经过期,再对数据库进行查询,并把查询到的对象,放进缓存。如果数据库查询对象为空,则不放进缓存。
如果每次都查询一个不存在value的key,由于缓存中没有数据,所以每次都会去查询数据库,对db造成很大的压力。
- 解决方案
- 缓存空值
将数据库中的空值也缓存到缓存层中,这样查询该空值就不会再访问DB,而是直接在缓存层访问就行。
-
缺点:空值过期时间不太好确定
-
使用布隆过滤器
-
构建方法
- 使用redis的module加载外部so文件
- 优点:操作简单
- 缺点:
- 需要高版本的redis
- 容易形成大key
- 借助bitmap来实现,k个hash函数,创建n个bitmap(推荐)
- 优点:操作简单
- 缺点:
- 由于redis的字符串要求最大为512M,所以需要拆分多个key
- 扩容稍微复杂
- 可以自己本地来实现布隆过滤器的计算,计算完之后在存入redis
- 优点:自己操作更灵活
- 缺点:
- 流程复杂
- 需要额外服务重启或当机之后布隆过滤器丢失问题
优点
- 节省内存空间
- 插入和查询时间复杂度都为O(1)
缺点
- 布隆过滤器不支持删除
- 由于哈希冲突的原因,可能会出现假阳性
思考
- 布隆过滤器多适用于数据更新较少的场景,如果海量数据模式下,数据量又频繁变化,如何高效构建布隆过滤器呢?
- 使用mapreduce来并行执行
- 布隆过滤器如何支持删除操作呢?
- 计数布隆过滤器
- 布谷鸟过滤器

