import torch
from d2l.torch import d2l
from torch import nn

from padding import comp_conv2d


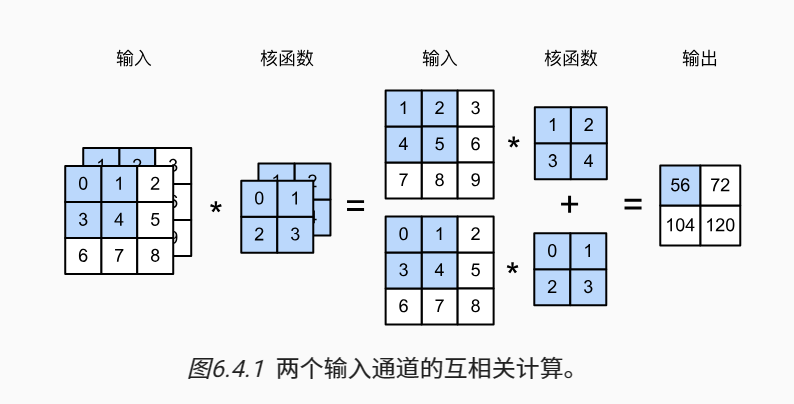
# 多输入通道的互相关运算
def corr2d_multi_in(X, K):
    # 先遍历X和K的第0个维度(通道维度), 再把它们加载一起
    return sum(d2l.corr2d(x, k) for x, k in zip(X, K))


X = torch.tensor([[[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]],
                  [[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]]])

K = torch.tensor([[[0.0, 1.0], [2.0, 3.0]],
                  [[1.0, 2.0], [3.0, 4.0]]])

print(corr2d_multi_in(X, K))


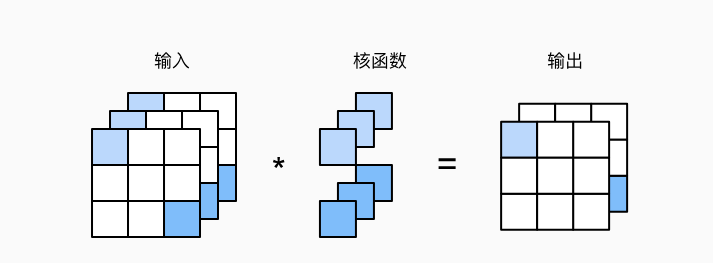
# 计算多个通道的输出的互相关函数
def corr2d_multi_in_out(X, K):
    return torch.stack([corr2d_multi_in(X, k) for k in K], 0)  # torch.stack函数将所有结果堆叠起来，形成一个多通道的输出张量。


K = torch.stack((K, K + 1, K + 2), 0)  # K被定义为一个包含三个卷积核的张量，其中每个卷积核与原始K张量的元素值递增1。
print(K.shape)
print(corr2d_multi_in_out(X, K))

1x1卷积，也称为网络中网络（NiN）操作，是一个在计算机视觉和深度学习中广泛使用的技术。其主要作用有两个方面：

连接通道：1x1卷积核的主要作用是实现跨通道的交互和信息整合，相当于全连接层的作用。对于输入特征图的每一个位置，通过1x1卷积核可以得到输出通道特征图的每一个位置，也就是说对于每一个位置，其可以看作是输入通道的线性组合。

调整维度：1x1卷积可以用来调整网络层之间的通道数目。比如，将256个通道的特征图转变成64个通道的特征图，减少参数数量，降低计算复杂度。

# 1x1卷积
def corr2d_multi_in_out_1x1(X, K):
    c_i, h, w = X.shape  # 输入通道数
    c_o = K.shape[0]  # 输出通道数
    X = X.reshape(c_i, h * w)
    K = K.reshape(c_o, c_i)
    # 全连接层中的矩阵乘法
    Y = torch.matmul(K, X)
    return Y.reshape(c_o, h, w)


X = torch.normal(0, 1, (3, 3, 3))
K = torch.normal(0, 1, (2, 3, 1, 1))

Y1 = corr2d_multi_in_out_1x1(X, K)
Y2 = corr2d_multi_in_out(X, K)
assert float(torch.abs(Y1 - Y2).sum()) < 1e-6

首先，根据X的形状，我们可以得知输入通道数c_i，以及图片的高和宽h，w。

然后，我们将X的形状从(c_i，h，w)转化为(c_i，h*w)。简单来说，就是将三维变量X调整为二维，方便进行线性代数运算。

同样的，我们也将K的形状从(c_o，c_i, 1, 1)转化为(c_o,c_i)，也就是将四维变量K调整为二维。

接着，我们使用torch.matmul(K, X)进行矩阵乘法。K作为第一个参数，代表矩阵乘法的左操作数；X作为第二个参数，代表矩阵乘法的右操作数。

最后，我们将得到的结果Y调整为所需的输出形状(c_o, h, w)。

代码的最后部分是对比1x1卷积和普通卷积的计算结果是否一致。如果一致，那么我们可以认为corr2d_multi_in_out_1x1函数的实现是正确的。