已完结www
AcWing116. 飞行员兄弟
由于每个把手最多只可能进行一次操作,所以我们可以枚举每个把手是否操作。
为了方便枚举,我们可以把 $+$ 当成 $1$,$-$ 当成 $0$,然后二进制枚举 $0$ 到 $2^{16} - 1$,然后判断该操作是否合法。
假设对于 $0000\ 0100\ 0000\ 0000$ 的 $1$ 进行了操作,那么我们应该把第 $2, 5, 6, 7, 8, 10, 14$ 位进行改变。
我们可以预处理出一个 $row_i$ 表示对于第 $i$ 行的所有数 $k_1,k_2,k_3,k_4$,令 $row_i = 2^{k_1} + 2^{k_2} + 2^{k_3} + 2^{k_4}$,同样的再预处理出维护列的 $col_i$,那么如果我们对第 $i$ 位进行了操作,那么我们只需要做 t ^= row[i / 4] + col[i % 4] - (1 << i) 即可。
时间复杂度为:$O(2^{16} \times 16)$
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 10, M = 16;
int g, ans = 0x3f3f3f3f, ansg;
int row[N], col[N];
int check(int state) {
int ans = 0, t = g;
for (int i = 0; i < M; i ++)
if (state >> i & 1) {
ans ++;
int change = row[i / 4] + col[i % 4] - (1 << i);
t ^= change;
}
for (int i = 0; i < M; i ++)
if (t >> i & 1) ans = 0x3f3f3f3f;
return ans;
}
int main() {
for (int i = 0; i < 4; i ++)
for (int j = 0; j < 4; j ++)
row[i] |= (1 << (i * 4 + j));
for (int j = 0; j < 4; j ++)
for (int i = 0; i < 4; i ++)
col[j] |= (1 << (i * 4 + j));
for (int i = 0; i < 4; i ++)
for (int j = 0; j < 4; j ++) {
char c; cin >> c;
if (c == '+') g |= 1 << (i * 4 + j);
}
for (int i = 0; i < 1 << M; i ++) {
int r = check(i);
if (ans > r) ans = r, ansg = i;
}
cout << ans << endl;
for (int i = 0; i < M; i ++)
if (ansg >> i & 1)
cout << i / 4 + 1 << ' ' << i % 4 + 1 << endl;
return 0;
}
AcWing117. 占卜DIY
双端队列模拟,没什么好写的。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 15;
deque<int> q[15];
int cnt[N];
int main() {
for (int i = 1; i <= 13; i ++) {
for (int j = 1; j <= 4; j ++) {
char c; cin >> c;
if (c == 'J') q[i].push_back(11);
else if (c == 'Q') q[i].push_back(12);
else if (c == 'K') q[i].push_back(13);
else if (c == 'A') q[i].push_back(1);
else q[i].push_back(c == '0' ? 10 : c - '0');
}
}
int die = 0, u = q[13].front();
q[13].pop_front();
while (die < 4) {
if (u == 13) {
die ++;
u = q[13].front();
q[13].pop_front();
continue;
}
q[u].push_front(u);
int now = u;
u = q[u].back();
q[now].pop_back();
if (cnt[now] < 4) cnt[now] ++;
}
int res = 0;
for (int i = 1; i <= 13; i ++)
res += cnt[i] == 4;
cout << res << endl;
return 0;
}
AcWing118. 分形
找规律,我们可以发现第 $i$ 层一共有 $3^{i - 1}$ 行,并且可以用五个上一层的图形进行拼接而成。
我们找到每个图形的左上角坐标,分别为 $(1, 1),(1, 3^{i - 2}\times 2 + 1),(3^{i - 2} + 1,3^{i - 2} + 1),(3^{i - 2}\times 2 + 1, 1), (3^{i - 2}\times 2 + 1, 3^{i - 2}\times 2 + 1)$
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 800;
char g[N][N][8];
int pow3(int x) {
int res = 1;
for (int i = 1; i <= x; i ++) res *= 3;
return res;
}
void work(int k, int x1, int y1) {
for (int i = 1; i <= pow3(k - 2); i ++)
for (int j = 1; j <= pow3(k - 2); j ++)
g[x1 + i - 1][y1 + j - 1][k] = g[i][j][k - 1];
}
int main() {
for (int k = 1; k <= 7; k ++)
for (int i = 1; i <= pow3(k - 1); i ++)
for (int j = 1; j <= pow3(k - 1); j ++)
g[i][j][k] = ' ';
g[1][1][1] = 'X';
for (int i = 2; i <= 7; i ++) {
work(i, 1, 1);
work(i, 1, pow3(i - 2) * 2 + 1);
work(i, pow3(i - 2) + 1, pow3(i - 2) + 1);
work(i, pow3(i - 2) * 2 + 1, 1);
work(i, pow3(i - 2) * 2 + 1, pow3(i - 2) * 2 + 1);
}
int n;
while (cin >> n && ~n) {
for (int i = 1; i <= pow3(n - 1); i ++, puts(""))
for (int j = 1; j <= pow3(n - 1); j ++)
printf("%c", g[i][j][n]);
puts("-");
}
return 0;
}
AcWing119. 袭击
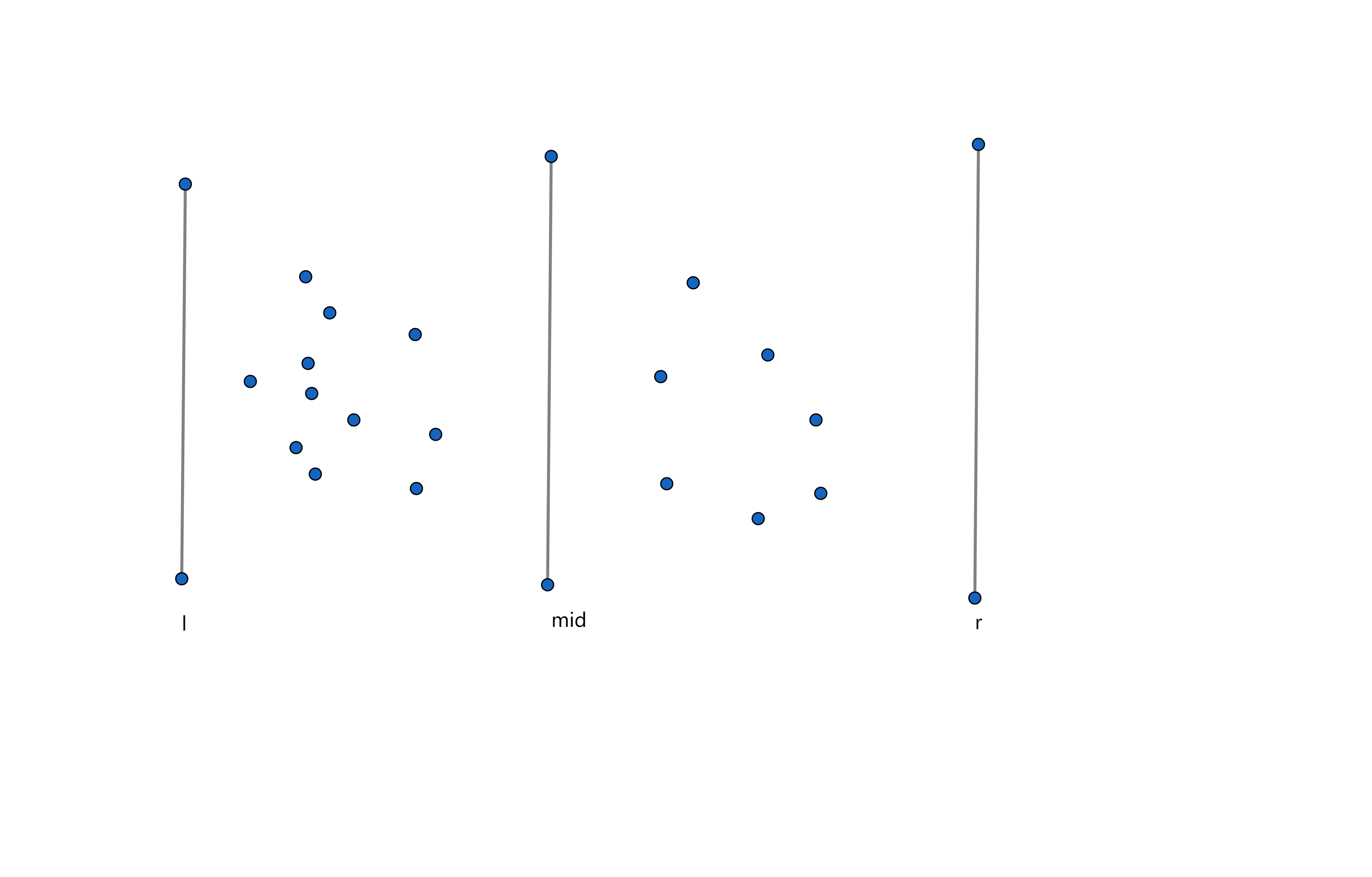
如上图,我们可以把区间根据 $x$ 分为两个部分,这样我们只要能够求出从 $[l,mid]$ 中选出一个点和从 $[mid + 1, r]$ 中选出一个点的最小距离。
首先,我们令当前最小距离 $res = \min(dfs(l, mid), dfs(mid + 1, r))$,如下图
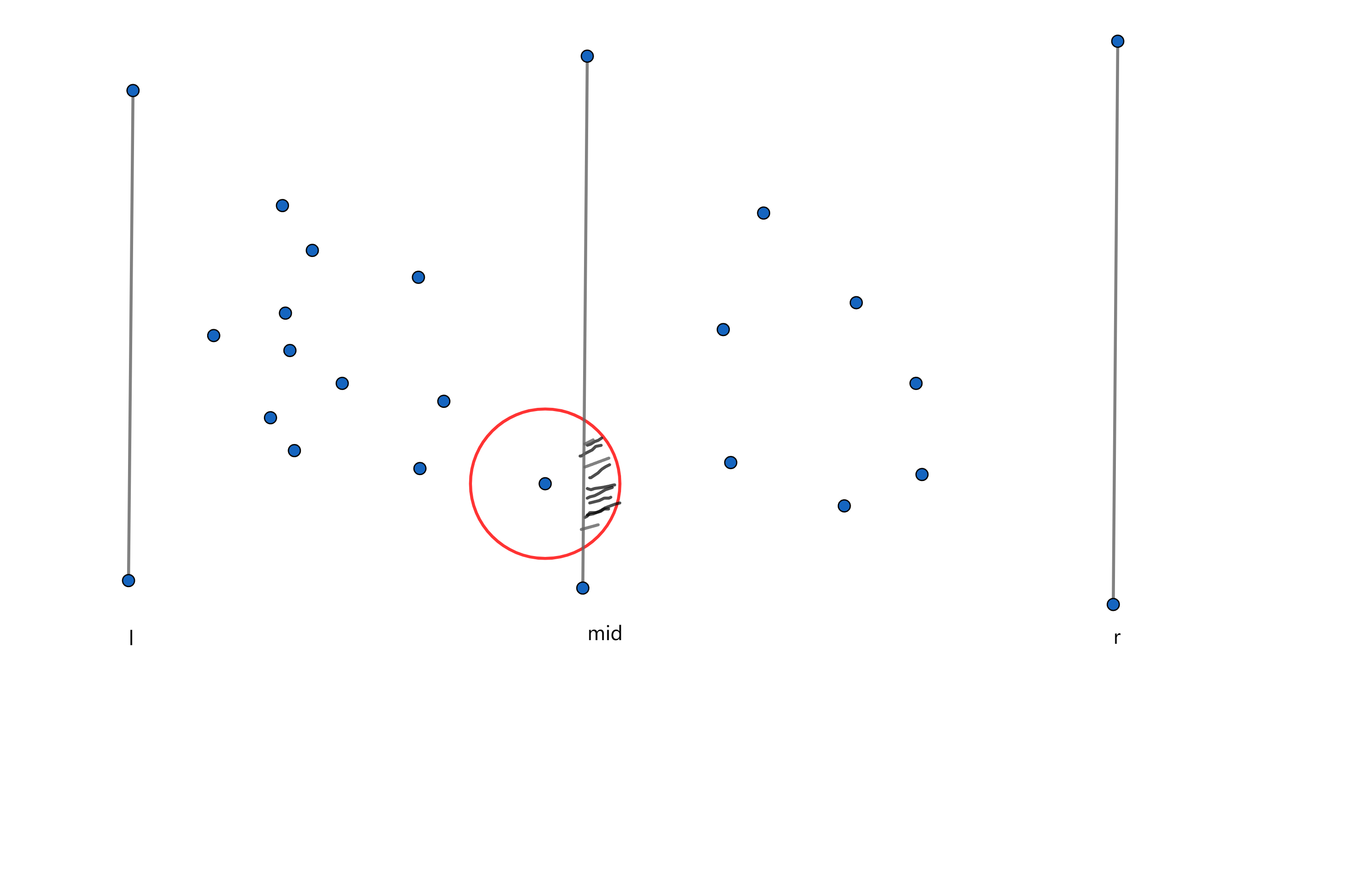
我们只需要求出阴影范围内的点即可。
这里有一个性质:对于一个左边的点,右边最多只有 $6$ 个点会被考虑。
证明:如下图。
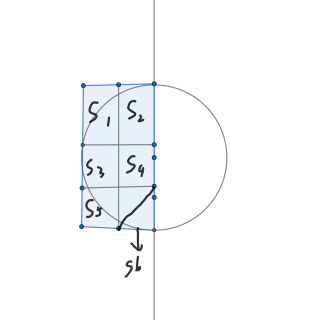
假设当前有 $7$ 个点被考虑,那么根据抽屉原理,一定会有两个点在同一个格子里。我们发现大长方形的宽为 $r$,长为 $2r$,所以小长方形的长为 $\frac{2}{3}r$,宽为 $\frac{1}{2}r$,那么在长方形内部的最长距离也就是对角线长度为 $\sqrt{(\frac{2}{3}r)^2 + (\frac{1}{2}r) ^ 2} = \frac{5}{6}r < r = ans$,所以不可能有 $7$ 个点。
所以我们每次枚举会枚举 $6$ 个点,复杂度为 $O(6n)$,总复杂度为 $O(nlogn)$
由于一些奇怪的有序的数据会使我们的 $sort$ 退化成 $O(n^2)$,所以我们要在排序前先打乱一下数组。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 200010, INF = 0x3f3f3f3f;
int T, n, m;
double ans;
struct node {
double x, y;
int type;
} points[N], tmp[N];
double dist(node a, node b) {
if (a.type == b.type) return INF;
return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}
double dfs(int l, int r) {
if (l == r) return INF;
int mid = l + r >> 1;
double midx = points[mid].x;
double res = min(dfs(l, mid), dfs(mid + 1, r));
int k = 0, i = l, j = mid + 1;
while (i <= mid && j <= r)
if (points[i].y < points[j].y) tmp[k ++] = points[i ++];
else tmp[k ++] = points[j ++];
while (i <= mid) tmp[k ++] = points[i ++];
while (j <= r) tmp[k ++] = points[j ++];
for (int i = l; i <= r; i ++) points[i] = tmp[i - l];
k = 0;
for (int i = l; i <= r; i ++)
if (points[i].x >= midx - res && points[i].x <= midx + res)
tmp[k ++] = points[i];
for (int i = 0; i < k; i ++)
for (int j = i - 1; j >= 0 && tmp[i].y - tmp[j].y < res; j --)
res = min(res, dist(tmp[i], tmp[j]));
ans = min(ans, res);
return res;
}
int main() {
scanf("%d", &T);
while (T --) {
scanf("%d", &n);
for (int i = 0; i < n; i ++) {
scanf("%lf%lf", &points[i].x, &points[i].y);
points[i].type = 0;
}
for (int i = n; i < n * 2; i ++) {
scanf("%lf%lf", &points[i].x, &points[i].y);
points[i].type = 1;
}
n *= 2;
random_shuffle(points, points + n);
sort(points, points + n, [&](node a, node b){
return a.x < b.x;
});
ans = dist(points[0], points[n - 1]);
double res = dfs(0, n - 1);
printf("%.3lf\n", res);
}
return 0;
}
AcWing120. 防线
考虑到防线上最多只有一个奇数防具,所以我们可以二分,如果 $[l,mid]$ 的和为奇数,就代表奇数在这段区间内 $r = mid$,否则 $l = mid + 1$。
那么如何快速计算 $[l,mid]$ 的和呢?我们可以用到前缀和思想。
考虑如何计算 $[mins, x]$ 之间的和。
我们可以枚举每一个等差数列 $p[i]$,如果 $p[i].s \leq x$ 说明两个区间存在交集,那么交集应该为 $[p[i].s, min(p[i].e, x)]$。
根据小学奥数,交集内部的数量就应该为(末项-首项)/ 公差 + 1,即 $(min(p[i].e,x) - p[i].s) \div p[i].d + 1$。
所以 $[l, mid]$ 的和就等于 $calc(mins, mid) - calc(mins, l)$ 。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 200010;
int T, n;
int s[N];
struct node {
int s, e, d;
} p[N];
int calc(int x) {
int res = 0;
for (int i = 1; i <= n; i ++)
if (p[i].s <= x)
res += (min(p[i].e, x) - p[i].s) / p[i].d + 1;
return res;
}
int main() {
scanf("%d", &T);
while (T --) {
int l = 0x3f3f3f3f, r = -0x3f3f3f3f;
scanf("%d", &n);
for (int i = 1; i <= n; i ++) {
scanf("%d%d%d", &p[i].s, &p[i].e, &p[i].d);
l = min(l, p[i].s);
r = max(r, p[i].e);
}
if (calc(r) & 1) {
while (l < r) {
int mid = l + r >> 1;
if ((calc(mid) - calc(l - 1)) & 1) r = mid;
else l = mid + 1;
}
printf("%d %d\n", l, calc(l) - calc(l - 1));
} else {
puts("There's no weakness.");
}
}
return 0;
}
AcWing121. 赶牛入圈
先把 $X,Y$ 坐标离散化,然后计算离散化后的前缀和。接着我们考虑二分正方形边长,该二分正确性显然,因为在满足条件的情况下边长变大答案不可能更优,而不满足条件时边长一定会增大。
考虑如何写 $check$ 函数。
由于我们已经预处理好了前缀和,我们就可以枚举正方形的左上角和右下角,然后通过前缀和来计算答案。一个细节是,因为四叶草的坐标是格子的左下角,所以我们在计算是要用 $x1 - x0 + 1$ 和 $y1 - y0 + 1$(建议画图)。
一个更细节的细节是,我们没必要一定枚举正方形,我们发现如果一个长方形的长和宽都小于等于正方形的边长,并且长方形内的四叶草数量大于等于 $c$,那正方形情况也一定成立。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef pair<int, int> PII;
#define x first
#define y second
const int N = 1010;
int c, n;
int s[N][N];
PII p[N];
vector<int> nums;
int find(int x) {
int l = 0, r = nums.size() - 1;
while (l < r) {
int mid = l + r >> 1;
if (nums[mid] >= x) r = mid;
else l = mid + 1;
}
return l;
}
bool check(int l) {
for (int x0 = 0, x1 = 1; x1 < nums.size(); x1 ++) {
while (nums[x1] - nums[x0 + 1] + 1 > l) x0 ++;
for (int y0 = 0, y1 = 1; y1 < nums.size(); y1 ++) {
while (nums[y1] - nums[y0 + 1] + 1 > l) y0 ++;
if (s[x1][y1] - s[x1][y0] - s[x0][y1] + s[x0][y0] >= c)
return true;
}
}
return false;
}
int main() {
scanf("%d%d", &c, &n);
nums.push_back(0);
for (int i = 1; i <= n; i ++) {
scanf("%d%d", &p[i].x, &p[i].y);
nums.push_back(p[i].x);
nums.push_back(p[i].y);
}
sort(nums.begin(), nums.end());
nums.erase(unique(nums.begin(), nums.end()), nums.end());
for (int i = 1; i <= n; i ++) {
int x = find(p[i].x), y = find(p[i].y);
s[x][y] ++;
}
for (int i = 1; i < nums.size(); i ++)
for (int j = 1; j < nums.size(); j ++)
s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
int l = 1, r = 10000;
while (l < r) {
int mid = l + r >> 1;
if (check(mid)) r = mid;
else l = mid + 1;
}
printf("%d\n", l);
return 0;
}
AcWing122. 糖果传递
七夕祭缩减版。推导过程不再写了。
#include <iostream>
#include <cstring>
#include <algorithm>
typedef long long LL;
using namespace std;
const int N = 1000010;
int n, a[N], w[N], s[N];
int main() {
scanf("%d", &n);
LL avg = 0;
for (int i = 1; i <= n; i ++) {
scanf("%d", &a[i]);
avg += a[i];
}
avg /= n;
for (int i = 1; i <= n; i ++)
w[i] = a[i] - avg;
for (int i = 1; i <= n; i ++)
s[i] = s[i - 1] + w[i];
sort(s + 1, s + 1 + n);
int k = n + 1 >> 1;
long long res = 0;
for (int i = 1; i <= n; i ++)
res += abs(s[i] - s[k]);
printf("%lld\n", res);
return 0;
}
AcWing123. 士兵
很容易发现我们可以把 $x$ 和 $y$ 分开来做。
首先考虑 $y$ 轴,排序后就是货仓选址。
再考虑 $x$ 轴,此处有一个性质是最优情况下,排序后士兵间的相对顺序和最后走到最终位置的相对顺序不会改变。
比如最左边的点走到 $p_1 = k$,则第 $i$ 个人走到 $p_i = k + (i - 1)$。
所以第 $i$ 个士兵(设其坐标为 $x_i$)要走的距离就是 $|x_i - [(k + (i - 1))]| = |x_i - (i - 1) - k|$
所以问题又变为了货仓选址,我们只需要给每个 $x_i - i$ 即可。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef pair<int, int> PII;
#define x first
#define y second
const int N = 10010;
int n, c[N];
PII p[N];
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i ++)
scanf("%d%d", &p[i].x, &p[i].y);
sort(p + 1, p + 1 + n, [&](PII a, PII b) {
return a.y < b.y;
});
int k = p[n + 1 >> 1].y;
int res = 0;
for (int i = 1; i <= n; i ++)
res += abs(p[i].y - k);
sort(p + 1, p + 1 + n, [&](PII a, PII b) {
return a.x < b.x;
});
for (int i = 1; i <= n; i ++)
p[i].x -= i - 1;
sort(p + 1, p + 1 + n, [&](PII a, PII b) {
return a.x < b.x;
});
k = p[n + 1 >> 1].x;
for (int i = 1; i <= n; i ++) {
res += abs(p[i].x - k);
}
printf("%d\n", res);
return 0;
}
AcWing124. 数的进制转换
高精度 + 模拟进制转换,没什么好写的,注意细节就行了。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 500;
int n, m, T;
string s, t;
int get(char c) {
if (c >= '0' && c <= '9') return c - '0';
else if (c >= 'A' && c <= 'Z') return c - 'A' + 10;
else return c - 'a' + 36;
}
char reget(int c) {
if (c <= 9) return c + '0';
else if (c < 36) return c - 10 + 'A';
else return c - 36 + 'a';
}
vector<int> div(vector<int> A, int b, int &r) {
vector<int> C;
r = 0;
for (int i = A.size() - 1; i >= 0; i --) {
r = r * n + A[i];
C.push_back(r / b);
r %= b;
}
reverse(C.begin(), C.end());
while (C.back() == 0 && C.size() > 0) C.pop_back();
return C;
}
int main() {
cin >> T;
while (T --) {
cin >> n >> m >> s;
cout << n << ' ' << s << endl << m << ' ';
vector<int> res, ans;
for (int i = s.size() - 1; i >= 0; i --)
res.push_back(get(s[i]));
while (res.size()) {
int r;
res = div(res, m, r);
ans.push_back(r);
}
for (int i = ans.size() - 1; i >= 0; i --)
cout << reget(ans[i]);
cout << endl << endl;
}
return 0;
}
AcWing125. 耍杂技的牛
将 $s + w$ 进行排序,证明类似国王游戏,这里不过多赘述。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 50010;
int n;
struct node {
int s, w;
} a[N];
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i ++)
scanf("%d%d", &a[i].w, &a[i].s);
sort(a + 1, a + 1 + n, [&](node a, node b) {
return a.w + a.s < b.w + b.s;
});
long long res = -0x3f3f3f3f, sum = 0;
for (int i = 1; i <= n; i ++) {
res = max(res, sum - a[i].s);
sum += a[i].w;
}
printf("%d\n", res);
return 0;
}
AcWing126. 最大的和
我们先预处理矩阵的前缀和,朴素思路是枚举矩阵的左上角和右下角,这样时间复杂度是 $O(n^4)$。
我们考虑优化,只枚举矩阵的起始行和结尾行,即 $x_1$ 和 $x_2$,然后用类似最长连续子段和的思路从 $1$ 开始枚举列,找到最大连续列的和。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 110;
int n, g[N][N];
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i ++)
for (int j = 1; j <= n; j ++) {
scanf("%d", &g[i][j]);
g[i][j] += g[i - 1][j];
}
int res = -0x3f3f3f3f;
for (int i = 1; i <= n; i ++)
for (int j = i; j <= n; j ++) {
int last = 0;
for (int k = 1; k <= n; k ++) {
last = max(last, 0) + g[j][k] - g[i - 1][k];
res = max(res, last);
}
}
printf("%d\n", res);
return 0;
}
AcWing127. 任务
我们发现时间对收入的影响比级别多的多的多,所以我们以时间为第一关键字,收入为第二关键字从大到小排序任务和机器。
我们从 $1$ 到 $n$ 枚举每个任务,接着寻找每个可以使用的机器,并且使用其中级别最小的机器。
因为任务排过序,所以如果一台机器能满足当前任务的时间,就一定能满足之后所有任务的时间,但级别却不一定满足,所以我们需要使用可行机器里级别最小的。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <set>
using namespace std;
typedef long long LL;
const int N = 100010;
int n, m;
struct node {
int x, y;
} a[N], b[N];
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++)
scanf("%d%d", &a[i].x, &a[i].y);
for (int i = 1; i <= m; i ++)
scanf("%d%d", &b[i].x, &b[i].y);
sort(a + 1, a + 1 + n, [&](node a, node b) {
return a.x > b.x || a.x == b.x && a.y > b.y;
});
sort(b + 1, b + 1 + m, [&](node a, node b) {
return a.x > b.x || a.x == b.x && a.y > b.y;
});
multiset<int> S;
LL res = 0, cnt = 0;
for (int i = 1, j = 1; i <= m; i ++) {
while (j <= n && b[i].x <= a[j].x)
S.insert(a[j ++].y);
auto it = S.lower_bound(b[i].y);
if (it != S.end()) {
cnt ++;
res += b[i].x * 500 + b[i].y * 2;
S.erase(it);
}
}
printf("%lld %lld\n", cnt, res);
return 0;
}



不是亲,您初二了,时间咋这么多。是fzyz给你布置的作业太少了吗。
我现在每天 16:50 放学www
啊,你是yyzm啊,我说怎么会知道我在fzyz
fzyz作业确实少awa,我一般数学课和英语课写作业,很多在学校就写完了www
你们没有四五节辅导课的?
那个可以自己报名的,我只去数学和物理awa