众数问题

朴素方法：

对n的范围以及集合中元素的数值范围进行讨论
1 < n < 1000000;-1000000 < ai < 1000000

#include<iostream>
using namespace std;

const int N = 1e6+10;
int a[2*N];
int main(){
    int n;
    cin >> n;
    for(int i = 0;i < n;i ++){
        int x;
        scanf("%d",&x);
        a[(x+2*N) %(2*N)] ++;
    }
    int res = 0,index = -1; 
    for(int i = 0;i < 2*N;i ++){
        if(res < a[i]) {
            res = a[i];
            index = i > N ? i-2*N : i;  // 分正数和负数两种情况进行讨论
        }
    }
    cout<< index <<" "<< res <<endl;
    return 0;
}

时间复杂度O(N)空间复杂度O(N)
方法的缺点分析：集合元素的数值范围不能太大，集合元素的值域被限制在整数集中

分治法求解

时间复杂度分析O(nlogn)
空间复杂度O(n)
基本思路：划分集合，求独立子集上的众数，最后合并结果

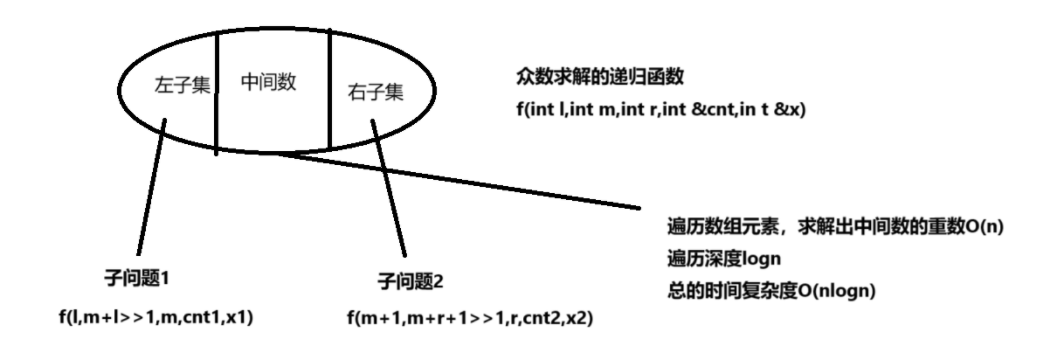
#include<iostream>
using namespace std;

const int N=1e6+10;
int a[N];
void func(int l,int r,int* cnt,int* x){
    if(l >= r) {
        *cnt=1,*x=a[r];
        return;
    }
    int m = l+r >>1; //划分集合
    int cnt1,x1,cnt2,x2;
    func(l,m-1,&cnt1,&x1);
    func(m+1,r,&cnt2,&x2);
    int val = a[m];
    *cnt=0,*x=val;
    // 求解基准数的重数
    for(int i = l;i <= r;i++)
        if(a[i] == val) (*cnt)++;
    if(cnt1 > *cnt) *cnt = cnt1,*x = x1;
    if(cnt2 > *cnt) *cnt = cnt2,*x = x2;
}



int main(){
    int n;
    cin>>n;
    for(int i=0;i<n;i++)
        scanf("%d",&a[i]);
    int cnt,x;
    // 确定集合中元素重数最大的数值，计算机数值的重数需要重新遍历集合
    func(0, n-1, &cnt, &x);
    cnt = 0;
    for(int i = 0;i < n;i ++){
        if(a[i] == x) cnt += 1;
    }
    cout << endl;
    cout<<x<<" "<<cnt<<endl;
    return 0;
}

测试数据

9
6 1 2 2 2 3 5 2 3