图论一小部分算法正确性证明/理解 (暂空)
非题解,只是给自己理解记忆用,log一下
图的遍历的问题感觉需要100道题.熟记于心,理解掌握.
10道经典题,90道技巧和练习.
100小时? (划掉,前一百小时只是感觉,猜测1000+hrs才勉强做够)
目录:
慢慢更新: 基础课dfs✅, bfs✅,三大问题✅ + 提高课(提高课图论就随便写十题就好, 今年先不用太纠结,当消遣就好)
lyd 0x60 图论 (竞赛级,≈ 或 大于 提高课难度)
1. DFS 深度优先搜索
DFS 暴力枚举 $O(N!)$ (第一位置$O(N)$,第二位置$O(N - 1)$,以此类推 N*(N-1)*(N-2)*...*1次计算)
这个递归的原理还是有点不理解。 $\color{pink}{我想应该是循环嵌套的逻辑,一层标记一个,恢复一个步骤}$(中间还要干事和进入下一层)
疑问: dfs这个state每次循环是怎么变化的。
迭代可以理解为按顺序循环,而递归的话还挺反直觉。
终止条件√ 这个可以理解: u 等于n时即第n步,已经把n个位置填完,输出
$\color{pink}{回溯过程}$ × 不太能理解: u 小于n步时:
经典DFS- 全排列问题:
我们需要填n个数。输出所有排列方案。
我想要按 顺序 枚举
根节点分叉有n个的数:
第一个数填1,第二个数填(2, 3, 4,…n) 【选择列表】
第一个数填2,第二个数填(1, 3, 4,…n)
每一(i-th)层表示第i个数填的东西
y总回溯算法模板:(即dfs)
void dfs(int u)
{
if 终止条件 return
for (int i = 1; i <= n; i++)
if (st[i] == false)
{
path[u] = i; //操作,因题而异
st[i] = true; //标记这个点已填过
dfs(u + 1); //进入下一步(填下一个数)
// 等递归结束后,把之前标记的填过的清空
//【这个递归还是挺难理解的】
path[u] = 0;
st[i] = false;
}
}
结论前置:
按照一颗多叉树来理解dfs回溯算法:每一层填第i位的数字。
path[u]即这一位(层)上填的数字,值为i,并将i的state标记为1 已填过,进入下一层,直到到底,然后一层层恢复状态.
例: 恢复一层以后 所有都还只有一种,继续上一重嵌套,再恢复一个现场,现在有两个位置了,又可以换顺序了,会有另外一种即dfs(n-1)层 i = 某值(n应该) 的state是0,可以填。(结合最后这两个位置来看即互换)
干完后继续恢复上一重,释放dfs(n-2)层
然后释放dfs(n - 3)
一直回溯到dfs(0)
开始最外围大循环的下一重i = 2. 第一个数填2,以此类推。((后面情况一样的)===> 此Theorem可将所有排列组合枚举到)数学归纳法表示n理论上可以是正整数的很大一个值,所以算法题都可以dfs。(我感觉应该达不到无穷,有限数和极限还是法则不太一样)
给自己的草稿,非讲解
模拟一遍吧:
首先 dfs(0)
进入循环 for里i从1到n
i = 1
st[1] = 0 (默认是否)
path[0] = 1
st[1] = true
dfs(1)
进入下一步
dfs(1)
i = 1, st[1] = 1不执行
i = 2, st[2] = 0 执行 (※)
path[1] = 2
dfs(2)
进入下一步,
i = 1, st[1]= 1
i = 2, st[2] = 1
i = 3, st[3] = 0执行
path[2] = 3
st[3] = 1
dfs(3)
进入下一步
3 == n 直接终止 输出 path[0, 1, 2]
恢复现场st[2] = 0, path[2] = 0
回到第二重嵌套循环内
承接(※)
dfs(1)里还剩一个
i = 3, st[3] = 0 执行
path[1] = 3
st[3] = 1
dfs(2)
进入下一步
i = 1, st[1] = 1
i = 2, st[2] = 0 执行
path[2] = 2
st[2] = 1
dfs(3) 3 == n 直接终止这一重循环
i = 3, st[3] = 1 不执行
恢复现场st[2] = 0
恢复现场st[1] = 0, path[1] = 1
回到第一重循环
dfs(0)
i = 2
一个套路。
然后十
i = 3
一样选法套路。
通过数学归纳法可以将这个理论扩展【泛化Without loss of Generalisation】到 n ∈ 正整数R* (如果不溢出的话)
$\huge{\color{cyan}{核心:}}$ 把选过的数从选择列表中删除,这样进入下一层(步)dfs时就会跳过已选的数
当所有选完后 dfs(u+1)后面的path[u] = 0, st[i] = false开始执行。将一路上选过的痕迹$\underline{一层一层}$恢复回初始的样子(毕竟只改了path和state两个数组,改回0就好啦)
而巧妙的在于一次只回溯到一层上,即如果_1 _ _ 除了12以外还可以填别的话,在这一层还可以继续保留第一位1 搜dfs(1)的剩下的循环。(i = 3的情况)
i = 1; i <= n; i++ 所有n重循环(和之中的(n-1)重和其中的(n-2)重…都会执行)
八皇后搜索原理一致。
使用递归Recursion和回溯来实现一条走到底的深搜。
并加入了下标状态转换(为截距)。
void dfs(int u)
{
if (u == n) {ans.push_back(path), return;} //题意要求输出棋盘(方案)
for (int i = 0; i < n; i ++)
{
if (!col[i] && !diag[u - i + n) && udiag[u + i]){
col[i] = diag[u - i + n] = udiag[u + i] = true;
path[u][i] = 'Q';
dfs(u + 1);
path[u][i] = '.';
col[i] = diag[u - i + n] = udiag[u + i] = false;
}
}
}
2. BFS:
情景 二维矩阵遍历:
使用队列,每次枚举四个方向。
首先队头head存上一个点的信息,队尾加入这一层的四个方向的信息。q[tail] = {x, y} 然后tail +=1 。
这样队列里的顺序就是一层一层的来。(每一层挨在一起)。
题目一般是①全都能走;②有些能走有些不能走。(障碍物),加进if判断就好。
二维用向量(偏移量来实现向四周遍历)
dx[4] = {-1, 0, 1, 0}; dy[4] = {0, 1, 0, -1}; // 上右下左
走路的时候 x + dx[i]; y + dy[i] 这样既可
3. 树和图的存储方式
| 有向图 | 无向图 |
|---|---|
| a -> b | a __ b |
| a -> b | |
| b -> a |
所以考虑有向图即可 $ a -> b $
方法:
① 邻接矩阵 g[a, b] 就开个二维数组,存 a -> b 这条边的信息,如果有权重就是权重,否则就是bool,true即有,false没有。
如果有重边,就保留其中一条即可。
② 邻接表 【单链表】Linked-List
如果有n个点,就开n个单链表。 【与拉链法存哈希表同方法】
存这个点可以走到哪个点 (路径)

例子:
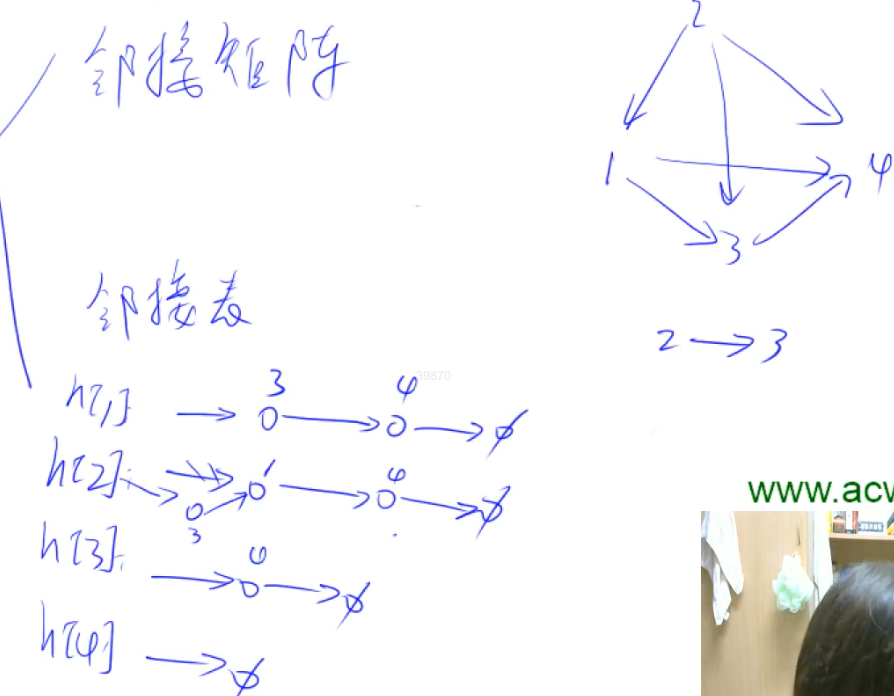
* 插入 add(int a, int b)* 函数即
将h[a] 的后面指向b,然后将b后面指向原来的a.next
(2-1-4-∅) 变为 (2-3-1-4-∅)
h 存所有链表头。 e 存所有节点的值, ne 存他的下一个(next指针)节点, index 序号, 到了哪个点了;
插入 a -> b
void add(int a, int b)
{
//在a所对应的单链表里插入一个节点b
e[index] = b; //节点b的值赋上。
ne[index] = h[a]; // 然后将next指针指向a的头结点
h[a] = index ++; //头结点更新为当前点,并序号到下一个点
}
后续慢慢更新
最短路问题,最小生成树,等

