最少费用购物问题

Dp求解问题

分析输入数据中仅仅包括n=2个物品情况，对于n=3、4、5……状态转移、状态表示方式类似
使用DP分析法：

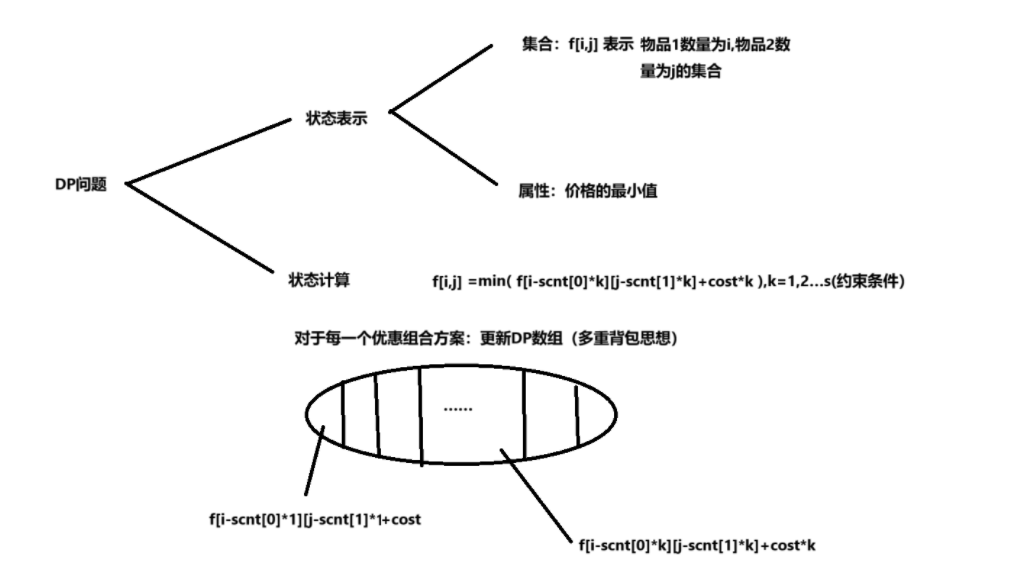
时间复杂度分析（联系多重背包问题）

#include<iostream>
#include<cstring>
using namespace std;

const int N=15;
int f2[N][N];
int seq[N],cnt[N],cost[N];  // 物品的编号，数量，花费
int scnt[N];

int find(int u){
    for(int i = 0;i < N;i ++){
        if(seq[i] == u) return i;
    }
    return -1;
}
int main(){
    int n,m;
    cin >> n;
    for(int i=0;i<n;i++){
        scanf("%d%d%d",&seq[i],&cnt[i],&cost[i]);
    }
    // 用朴素价格初始化状态数组
    switch(n){
        case 1:
            cout<<"error"<<endl;
            break;
        case 2:
            for(int i0=0;i0<=cnt[0];i0++)
                for(int i1=0; i1 <=cnt[1];i1++)
                    f2[i0][i1] = cost[0]*i0 + cost[1]*i1;
            break;
        case 3:
            cout<<"error"<<endl;
            break;
        case 4:
            cout<<"error"<<endl;         
            break;
        case 5:
            cout<<"erroe"<<endl;
    }
    for(int i=0;i<=cnt[0];i++){
        for(int j=0;j<=cnt[1];j++)
            cout<<f2[i][j]<<" ";
        cout<<endl;
    }
    cin >> m;
    while(m--){
        int k,cost;
        cin >> k;   // 优惠组中物品类型数
        memset(scnt,0,sizeof scnt);
        for(int i = 0,num,u;i < k;i ++){
            scanf("%d%d",&u,&num);
            int t = find(u);
            scnt[t] = num;
        }
        scanf("%d",&cost);  // 优惠组的总价值
        for(int j = 1,flag = 1; ;j ++){
            for(int i = 0;i < n;i ++){
                if(cnt[i] < j*scnt[i]) {
                    flag = 0;
                    break;
                }
            }
            if(!flag) break;    // 优惠组的条件不满足，跳出循环
            // 更新状态数组方式有问题，需要使用多重循环实现
            switch(n){
                case 1:
                    cout<<"error"<<endl;
                    break;
                case 2:
                    for(int i0=0;i0<=cnt[0];i0++)
                        for(int i1=0; i1 <=cnt[1];i1++)
                            if(i0>=j*scnt[0] && i1>=j*scnt[1]){
                                    f2[i0][i1] = min(f2[i0][i1],f2[i0-j*scnt[0]][i1-j*scnt[1]]+cost*j);
                                }
                    break;
                case 3:
                    cout<<"error"<<endl;
                    break;
                case 4:
                    cout<<"error"<<endl;         
                    break;
                case 5:
                    cout<<"error"<<endl;    
                    break;
            }


        }
    }
    // 输出所有物品的最小费用
    cout<<f2[cnt[0]][cnt[1]]<<endl;
    return 0;
}

输入数据

2
7 3 2
8 2 5
2
1 7 3 5
2 7 1 8 2 10