整数变化问题

深度优先遍历解空间搜索最优解

关于整数i的变换f和g定义如下：f(i)=3i; g(i)=i/2。
试设计一个算法，对于给定的2个整数n和m，用最少的f和g变换次数将n变换为m。
例如，可以将整数15用4次变换将它变换为整数4：4 = gfgg(15)。
并考虑当整数n不可能变换为整数m时，算法应该如何处理？(遍历所有的状态节点)

输入                     
15 4                      
输出                          
4
gfgg

分析思路如下：

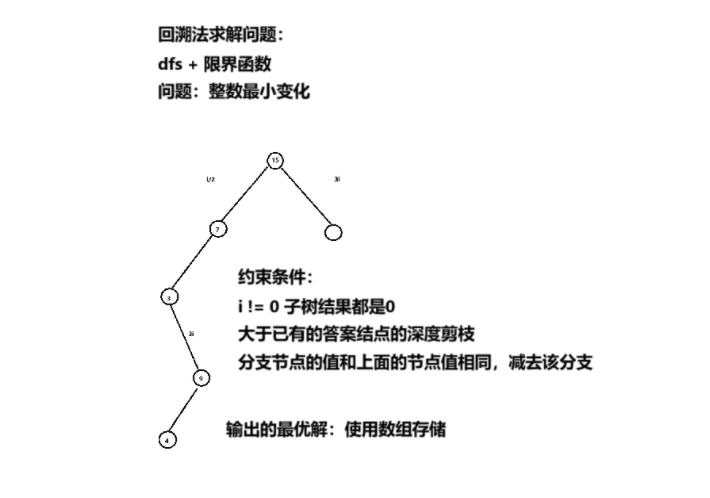
#include <iostream>
#include <cstring>
#include <set>

using namespace std;
const int N=110;
int source,target,L=0x3f3f3f3f;
int res[N],ans[N];   // 解数组
set<int> q;

void dfs(int u,int x){
    // 深度优先遍历递归终止条件
    if(x == 0 || u >= L) {
        // 整数变化为0或者不比当前解更优，需要进行剪枝
        return;
    }
    else if(x == target){
        L = u;  // 更新当前的最优解
        for(int i=0;i<u;i++)    ans[i]=res[i];
        return;
    }
    // 将数值x加入到遍历集合之中，用于冗余分支的剪枝
    q.insert(x);
    // 规定左子树进行i/2操作，右子树进行3*i操作
    if(!q.count(x/2)) {
        res[u] = 0;
        dfs(u+1,x/2);
    }
    if(!q.count(3*x)) {
        res[u] = 1;
        dfs(u+1,3*x);
    }
    q.erase(x); // 循环结束之后需要将该分支根节点上的数字删除，防止限制其他分支得纵深搜索
}  


int main(){
    cin>>source>>target;
    dfs(0,source);
    cout<<L<<endl;  // 实现最优解值计算
    // 构造最优解
    for(int i=0;i<L;i++)
        if(!ans[i]) cout<<"g";
        else cout<<"f";
    cout<<endl;
    return 0;
}