算法模板
目录
1. 排序
2. 二分
3. 高精度
(1) 高精度加
(2) 高精度减
(3) 高精度乘
(4) 高精度除
4. 前缀和与差分
(1) 一维前缀和
(2) 二维前缀和
(3) 一维差分
(4) 二维差分
5. 数据结构
(1) kmp
(2) Trie
(3) 并查集
(4) 堆
6. 搜索与图论
(1) DFS
(2) BFS
(3) Dijkstra朴素版
(4) Dijkstra堆优化版
(5) Bellman ford
(6) spfa求最短路
(7) spfa求负环
(8) Prim
(9) Kruskal
(10) 染色法判定二分图
(11) 匈牙利算法
7. 数学
(1) 判定质数
(2) 分解质因数
(3) 线性筛
(4) 求约数
(5) 约数个数
(6) 约数之和
(7) 最大公约数
(8) 欧拉函数
(9) 筛法求欧拉函数
(10) 快速幂
算法
排序
1. 快排
void quick_sort(int q[], int l, int r)
{
if(l >= r) return ;
int x = q[(l + r) / 2]; // 基准点
int i = l - 1, j = r + 1;
while(i < j)
{
do i++;while(q[i] < x);
do j--;while(q[j] > x);
if(i < j) swap(q[i] , q[j]);
}
quick_sort(q, l, j), quick_sort(q, j + 1, r);
}
2. 归并
void merge_sort(int l, int r)
{
if(l >= r) return ;
int mid = (l + r) / 2;
merge_sort(l, mid), merge_sort(mid + 1, r);
int i = l, j = mid + 1, k = 0;
while(i <= mid && j <= r)
{
if(q[i] <= q[j]) temp[k ++] = q[i ++];
else{
//cnt += mid - i + 1; 附加:cnt为逆序对数量
temp[k ++] = q[j ++];
}
}
while(i <= mid) temp[k ++] = q[i ++];
while(j <= r) temp[k ++] = q[j ++];
for(int i = l, j = 0; i <= r; i ++, j ++) q[i] = temp[j];
}
二分
while(l < r)
{
int mid = l + r >> 1;
if(q[mid] >= x) r = mid;
else l = mid + 1;
}
while(l < r)
{
int mid = l + r + 1 >> 1; //上取整
if(q[mid] <= x) l = mid;
else r = mid - 1;
}
高精度
1. 高精度加
vector<int> add(vetor<int> &A, vetor<int> &B)
{
int t = 0;
vector<int> C
for(int i = 0; i < A.size() || i < B.size(); i ++)
{
if(i < A.size()) t += A[i];
if(i < B.size()) t += B[i];
C.push_back(t % 10);
t /= 10;
}
if(t) C.push_back(1);
return C;
}
2. 高精度减
bool cmp(vector<int> &A, vector<int> &B)
{
if(A.size() != B.size()) return A.size() > B.size();
for(int i = A.size() - 1; i >= 0; i --)
if(A[i] != B[i])
return A[i] > B[i];
return true;
}
void sub(vector<int> &A, vector<int> &B) //这里前面需要判断A > B
{
int t = 0;
for(int i = 0; i < A.size(); i ++) // 由低位到高位
{
t = A[i] - t;
if(i < B.size()) t -= B[i];
C.push_back((t + 10) % 10); // 都默认进位10
if(t < 0) t = 1; // 如果为负,则说明前面确实进位了
else t = 0;
}
while(C.size() > 1 && C.back() == 0) C.pop_back(); // 去除前导0
}
3. 高精度乘
vector<int> mul(vector<int> A, int b)
{
vector<int> C;
int t = 0;
for(int i = 0; i < A.size() || t; i ++)
{
if(i < A.size()) t += A[i] * b;
C.push_back(t % 10);
t /= 10;
}
while(C.size() > 1 && C.back() == 0) C.pop_back(); //除去前导0
return C;
}
4. 高精度除
vector<int> div1(vector<int> A, int b, int &r) // A 是被除数, b是除数, r是余数
{
vector<int> C;
for(int i = A.size() - 1; i >= 0; i --)
{
r = r * 10 + A[i];
C.push_back(r / b);
r %= b;
}
reverse(C.begin(), C.end());
while(C.size() > 1 && C.back() == 0) C.pop_back(); // 高位可能会是0
return C;
}
前缀和
1.一维前缀和
for(int i = 1 ; i <= n ; i++) s[i] = s[i - 1] + q[i];
2.二维前缀和
// 构造方式
s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
// 求某一区间和方式
s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]
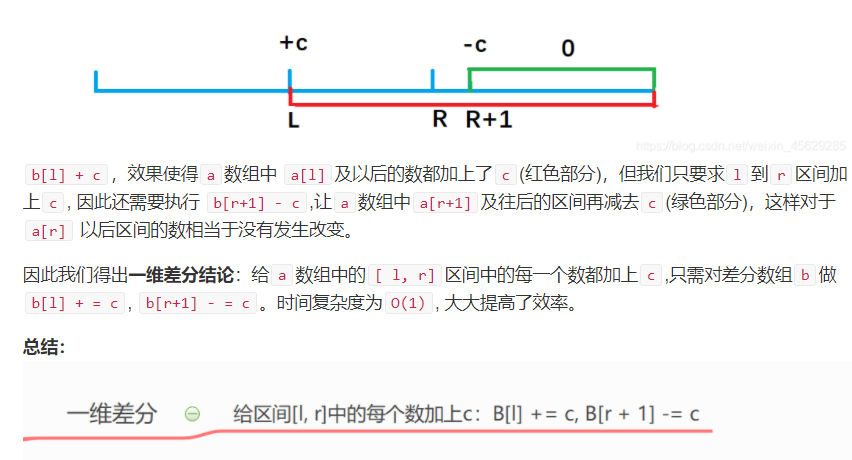
3.一维差分
// 构造方式
b[i] = a[i] - a[i - 1]; //构建差分数组
// 求解方式
b[l] += c; //将序列中[l, r]之间的每个数都加上c
b[r + 1] -= c;
// 得到处理以后的数组(前缀和)
a[i] = b[i] + a[i - 1];
引用一张题解大佬的图 题解
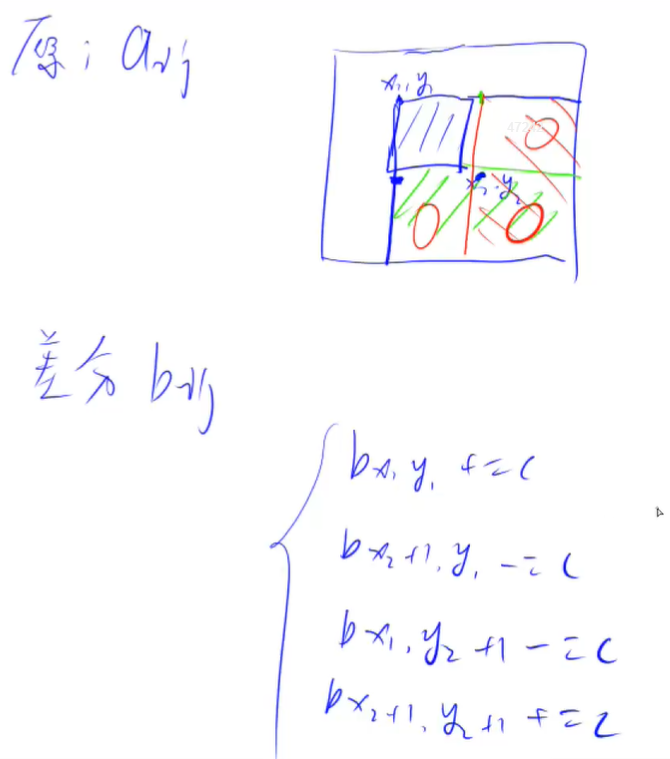
4.二维差分
// 差分函数
void insert(int x1, int y1, int x2, int y2, int c)
{
b[x1][y1] += c;
b[x1][y2 + 1] -= c;
b[x2 + 1][y1] -= c;
b[x2 + 1][y2 + 1] += c;
}
// 构造原数组
insert(i, j, i, j, a[i][j]);
// 构造差分数组
insert(x1, y1, x2, y2, c); //x1,y1为左上角,x2,y2为右下角
// 前缀和求解数组
b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
数据结构
1. kmp
//构造next数组
for(int i = 2, j = 0; i <= n; i ++)
{
while(j && p[j + 1] != p[i]) j = ne[j];
if(p[j + 1] == p[i]) j ++;
ne[i] = j;
}
//字符串匹配
for(int i = 1, j = 0; i <= m; i ++)
{
while(j && p[j + 1] != s[i]) j = ne[j];
if(p[j + 1] == s[i]) j ++;
if(j == n)
{
printf("%d ", i - n);
j = ne[j];
}
}
2. Trie
Trie树实际上是一颗多叉树,又叫字典树,是专门做字符串匹配的数据结构,用来 解决一组字符串中快速查找某个字符串的问题。
Trie字符串统计
// 变量定义
int son[N][26], idx; //q的一维是指该节点字母对应的asii码,二维是该节点所连接的结点,整体是指结点数
int cnt[N]; //存储每个结点的个数
char str[N];
// 建树
void insert(char str[])
{
int p = 0; //根结点,是空结点
for(int i = 0; str[i]; i ++)
{
int u = str[i] - 'a'; //将字母转换为对应的数字
if(!son[p][u]) son[p][u] = ++ idx; //新建一个结点
p = son[p][u];
}
cnt[p] ++; //该节点加一
}
// 查询
int query(char str[])
{
int p = 0;
for(int i = 0; str[i]; i ++)
{
int u = str[i] - 'a';
if(!son[p][u]) return 0;
p = son[p][u];
}
return cnt[p];
}
3. 并查集
int find(int x)
{
if(p[x] != x) p[x] = find(p[x]);
return p[x];
}
// p[find(a)] = find(b); 合并b成为父结点
//最重要是路径压缩才能使时间复杂度达到近乎O(1)
//也就是第一次查找后,会使每个节点的父节点变成祖宗节点
4.堆
//小根堆
//结点下移
void down(int u)
{
int t = u;
if(u * 2 <= cnt && h[u * 2] < h[t]) t = u * 2;
if(u * 2 + 1 <= cnt && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
if(u != t){
swap(h[u] , h[t]);
down(t);
}
}
//结点上移
void up(int u)
{
while(u / 2 && h[u / 2] > h[u])
{
swap(h[u / 2] , h[u]);
u /= 2;
}
}
//建堆
for(int i = n / 2; i ; i--) down(i);
搜索与图论
1. DFS
void dfs(int u){
st[u]=true; // 标记一下,记录为已经被搜索过了,下面进行搜索过程
for(int i=h[u];i!=-1;i=ne[i]){
int j=e[i];
if(!st[j]) {
dfs(j);
}
}
}
2. BFS
void bfs(PII u)
{
queue<int> q;
q.push(u);
st[u] = true;
int dx[]={-1,0,1,0}, dy[] = {0, 1, 0, -1};
while(q.size())
{
auto t = q.front();
q.pop();
for(int i = 0; i < 4; i ++)
{
int x = t.x + dx[i], y = t.y + dy[i];
// 判断扩展的点是否符合条件...
}
}
}
3.Dijkstra(朴素版)O($n^2$)
// dijkstra算法是求无负权边的最短路算法,它的算法思想是:更新每个点到起点的最短距离,那么,每次枚举除最后一// 个点以外的所有点,从中找到当前未确定的最短距离的点中距离最短的点,用它们更新其他点的最短距离
int dijkstra()
{
memset(dist , 0x3f , sizeof dist);
dist[1] = 0;
for(int i = 0 ; i < n - 1 ; i++){//因为最后更新的边距离是最远的,它无法用来更新其他点的距离
int t = - 1;
for(int j = 1 ; j <= n ; j++){
if(!st[j] && (t == -1 || dist[t] > dist[j]))
//如果当前点未更新过且该点到起始点的距离大于其他点到起始点的距离
t = j;
}
// 用找出的点来更新其他点到起点的最短距离
for(int j = 1 ; j <= n ; j++){
dist[j] = min(dist[j] , dist[t] + grah[t][j]); //当前j点与t点+权作比较
}
st[t] = true;
}
if(dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
4.Dijkstra(堆优化版)
贴一张题解区大佬的图

int dijkstra()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
priority_queue<PII, vector<PII>, greater<PII>> heap; //维护当前未在st中标记过且离源点最近的点
heap.push({0, 1});
while (heap.size())
{
//1、找到当前未在s中出现过且离源点最近的点
auto t = heap.top();
heap.pop();
int ver = t.second, distance = t.first;
if (st[ver]) continue;
//2、将该点进行标记
st[ver] = true;
//3、用t更新其他点的距离
for (int i = h[ver]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[ver] + w[i])
{
dist[j] = dist[ver] + w[i];
heap.push({dist[j], j});
}
}
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
5.Bellman_ford
struct edges{
int a, b, w;
}edge[M];
int dist[N], backup[N];
int bellman_ford()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
for(int i = 0; i < k; i++)
{
// 例如在1->2->3, 1->3 这个例子中,要是用dist[a]更新将会导致最后结果为2,但是走了两条边
memcpy(backup, dist, sizeof dist); //备份下,防止串联
for(int j = 0; j < m; j++)
{
int a = edge[j].a, b = edge[j].b, w = edge[j].w;
dist[b] = min(dist[b], backup[a] + w); //更新每个点的最小路径
}
}
if(dist[n] > 0x3f3f3f3f / 2) return -1;
return dist[n];
}
6.spfa求最短路
int spfa()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
queue<int> q;
q.push(1);
st[1] = true;
while(q.size())
{
auto t = q.front();
q.pop();
st[t] = false;
// 对松弛操作进行了优化
for(int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if(dist[j] > dist[t] + w[i]) // 找到更新过的值去更新其他点
{
dist[j] = dist[t] + w[i];
if(!st[j]){
st[j] = true;
q.push(j);
}
}
}
}
if(dist[n] == 0x3f3f3f3f) return -1;
else return dist[n];
}
7.spfa求负环
bool spfa()
{
queue<int> q;
dist[1] = 0;
// 该题是判断是否存在负环,并非判断是否存在从1开始的负环,因此需要将所有的点都加入队列中,更新周围的点
for(int i = 1; i <= n; i++)
{
st[i] = true;
q.push(i);
}
// cnt[x] 记录当前x点到虚拟源点最短路的边数
while(q.size())
{
auto t = q.front();
q.pop();
st[t] = false;
for(int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if(dist[j] > dist[t] + w[i])
{
dist[j] = dist[t] + w[i];
cnt[j] = cnt[t] + 1;
if(cnt[j] >= n) return true;
if(!st[j])
{
st[j] = true;
q.push(j);
}
}
}
}
return false;
}
8.prim
// 算法思想:将每个点到集合的距离初始化为正无穷
// 迭代n次,选出到集合距离最小的点,用它来更新其他点到集合的距离
int prim()
{
memset(dist, 0x3f, sizeof dist);
for(int i = 0; i < n; i ++)
{
int t = -1;
for(int j = 1; j < n; j ++)
if(!st[j] && (t == -1 || dist[t] > dist[j])
t = j;
if(i && dist[t] == INF) return INF; // 如果不是第一个点并且离集合最短的点不是正无穷
if(i) res += dist[t]; // 更新生成树权重,不能在更新其他点后面写,因为如果存在自环,dist[t]会更新
for(int j = 1; j < n; j ++)
dist[j] = min(dist[j], g[t][j]);
st[t] = true;
}
return res;
}
9.Kruskal
算法思想:1. 将所有边按照权重从小到大排序 O(mlog(m))
2. 枚举每条边(a, b, 权重c) O(m)
3. 如果a,b不连通,将a,b加入集合中
struct Edge{
int a , b , w;
bool operator<(const Edge& W) const{
return w < W.w;
}
}Edges[N];
int p[N];
int find(int x)
{
if(p[x] != x) p[x] = find(p[x]);
return p[x];
}
int kruskal
{
int cnt = 0, res = 0;
sort(Edges, Edges + m);
for(int i = 1; i <= n; i ++) p[i] = i;
for(int i = 0; i < m; i ++)
{
int a = Edges[i].a, b = Edges[i].b, w = Edges[i].w;
a = find(a), b = find(b);
if(a != b)
{
p[a] += b;
res += w;
cnt ++;
}
}
if(cnt < n - 1) return INF;
else return res;
}
10.染色法判定二分图
二分图:一条边的两个点一定属于不同的集合
二分图当且仅当图中不含奇数环
代码思路:
染色可以使用1和2区分不同颜色,用0表示未染色
遍历所有点,每次将未染色的点进行dfs, 默认染成1或者2
由于某个点染色成功不代表整个图就是二分图,因此只有某个点染色失败才能立刻break/return
染色失败相当于存在相邻的2个点染了相同的颜色
void dfs(int u, int c)
{
color[u] = c;
for(int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if(!color[j])//如果没有染上颜色,就染上
{
if(!dfs(j, 3 - c) return false;
}
else if(color[j] == c) return false; //如果染上,就判断是否有矛盾
}
return true;
}
11.匈牙利算法
这直接摘抄题解区dl的模板,感觉非常好理解 题解
//这个函数的作用是用来判断,如果加入x来参与模拟配对,会不会使匹配数增多
int find(int x)
{
//遍历自己喜欢的女孩
for(int i = h[x] ; i != -1 ;i = ne[i])
{
int j = e[i];
if(!st[j])//如果在这一轮模拟匹配中,这个女孩尚未被预定
{
st[j] = true;//那x就预定这个女孩了
//如果女孩j没有男朋友,或者她原来的男朋友能够预定其它喜欢的女孩。配对成功,更新match
if(!match[j]||find(match[j]))
{
match[j] = x;
return true;
}
}
}
//自己中意的全部都被预定了。配对失败。
return false;
}
数学
1. 判定质数O($logn$)
bool is_prime(int x)
{
if(x == 1) return false;
for(int i = 2; i <= x / i; i++)
if(x % i == 0)
return false;
return true;
}
2. 分解质因数
void put_prime(int x)
{
for(int i = 2; i <= x / i; i ++)
if(x % i == 0)
{
int s = 0;
while(x % i == 0)
{
x /= i;
s ++;
}
printf("%d %d\n", i, s);
}
if(x > 1) printf("%d %d\n", x, 1);
puts("");
}
3. 线性筛 $O(n)$
void get_primes(int n)
{
for(int i = 2; i <= n; i ++)
{
if(!st[i]) primes[cnt ++] = i;
for(int j = 0; primes[j] < n / i; j ++)
{
st[primes[j] * i] = true; // 每个合数一定是被它的最小质因子筛掉
//表明primes[j]一定是i的最小质因子,没有必要再遍历,primes要小于等于i的最小质因子
//这样能保证每个数遍历一遍,而没有重复
if(i % primes[j] == 0) break;
}
}
}
4.求约数
vector<int> get(int x)
{
vector<int> res;
for(int i = 1; i <= x / i; i++)
{
if(x % i == 0)
{
res.push_back(i);//加入较小的约数
if(i != x / i) res.push_back(x / i); //加入较大的约数
}
}
sort(res.begin(), res.end());
return res;
}
5.求约数个数
约数个数=$(a_1 + 1)(a_2 + 1)+…+(a_k + 1)$
$N = p_1^{a_1} * p_2^{a_2} * … * p_k^{a_k}$
$d = p_1^{β_1} * p_k^{β_k} * … * p_k^{β_k}$
每个约数对应一个$β_1 ~ β_k$组合,而$β_k$的取法又只有$a_k+1$种,由乘法定理可以得到答案
void get_num(int n)
{
while(n --)
{
int x;
cin >> x;
for(int i = 2; i <= x / i; i ++)
{
while(x % i == 0)
{
x /= i;
primex[i] ++;
}
}
if(x > 1) primes[x] ++;
}
//计算约数个数
ll res = 1;
for(auto prime : primes) res = res * (prime.second + 1) % mod;
printf("%d\n", res);
}
6.约数之和
约数之和=$(p_1^0 + p_1^1 + … + p_1^{a_1}) * … * (p_k^0 + p_k^1 + … + p_k^{a_k})$
//产生质因数
while(n --)
{
int x;
scanf("%d", &x);
for(int i = 2; i <= x / i; i++)
while (x % i == 0)
{
x /= i;
primes[i] ++;
}
if (x > 1) primes[x] ++;
}
//计算约数之和
ll res = 1;
for(auto prime : primes)
{
ll t = 1;
int p = prime.first , a = prime.second;
while(a --) t = (t * p + 1) % mod;
res = (res * t) % mod;
}
7.最大公约数(辗转相除法)
int gcd(int a, int b)
{
return b ? gcd(b, a % b) : a;
}
8.欧拉函数
$φ(N)$ $1-N$中与$N$互质的数的个数
$N = p_1^{a_1} * p_2^{a_2} … p_k^{a_k}$
$φ(N)$ = $N (1 - 1 / p_1)(1 - 1 / p_2)…(1 - 1 / p_k)$
void get_euler()
{
int res = x; // 记得要先乘n
for(int i = 2; i <= x / i; i ++)
{
if(x % i == 0)
{
while(x % i == 0) x /= i;
res = res / i * (i - 1);
}
if(x > 1) res = res / x * (x - 1);
}
}
9.筛法求欧拉函数
摘自 题解

void get_phi(int n)
{
for(int i = 2; i <= n; i ++)
{
if(!st[i])
{
primes[cnt ++] = i;
phi[i] = i - 1;
}
for(int j = 0; primes[j] <= n / i; j ++)
{
st[primes[j] * i] = true;
if(i % primes[j] == 0)
{
phi[i * primes[j]] = phi[i] * primes[j];
break;
}
phi[i * primes[j]] = phi[i] * primes[j] * (1 - 1 / primes[j]);
}
}
}
10.快速幂
int qmi(int a, int k, int p) // a ^ k % p
{
int res = 1;
while(k)
{
if(k & 1) res = (LL)res * a % p;
k >>= 1;
a = (LL)a * a % p;
}
}
11.扩展欧几里德
LL exgcd(int a, int b, int x, int y)
{
if(b == 0)
{
x = 1, y = 0;
return a;
}
LL x1, y1;
LL gcd = exgcd(b, a % b, x1, y1);
x = y1, y = x1 - (a / b) * y1;
return gcd;
}

