背包问题

算法思路：

线性规划一般用于求解出符合各约束条件的目标函数最优解。核心思想为通过组合子问题的解来求解原问题的解。总体而言求解是自上而下的（自原问题向子问题）。即从原问题中分解出子问题，然后列出其中状态转移方程，遍历所有状态，求得最优解。f[i][j]保存i,j处的状态。

时间复杂度：

一般为O(状态数量*转移计算量)。

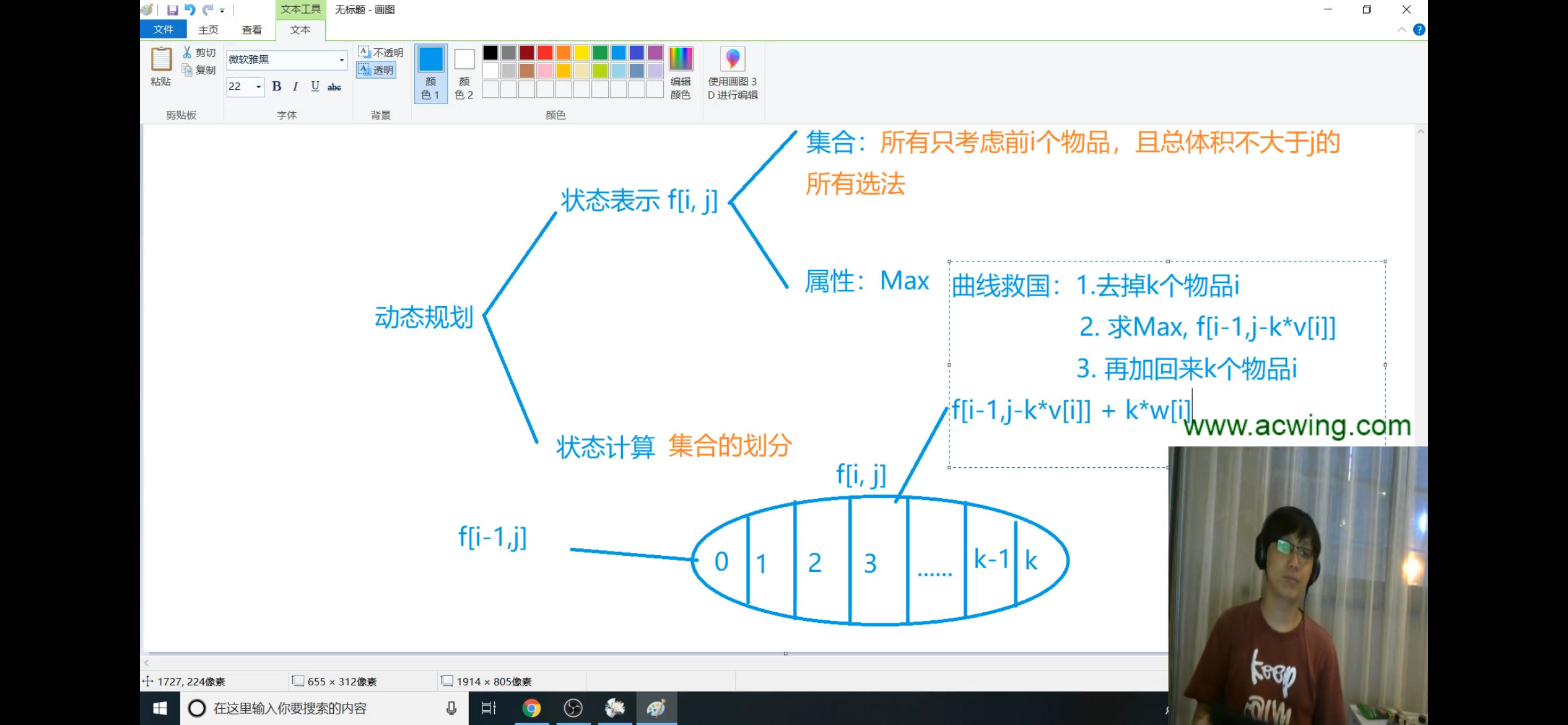
一、01背包

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 10010;

int v[N], w[N];
int f[N];

int main(){

    int n, m;
    cin >> n >> m;

    for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];

    for(int i = 1; i <= n; i++){
        for(int j = m; j >= v[i]; j--){
            f[j] = max(f[j], f[j - v[i]] + w[i]);
        }
    }

    cout << f[m] << endl;

    return 0;
}

二、完全背包

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 1e5;

int n, m;
int v[N], w[N];
int f[N];

int main(){
    cin >> n >> m;
    for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];

    for(int i = 1; i <= n; i++){
        for(int j = v[i]; j <= m; j++){
            f[j] = max(f[j], f[j - v[i]] + w[i]);
        }
    }

    cout << f[m] << endl;
    return 0;
}