图像压缩问题

数据结构

DP数组

算法

动态规划求解

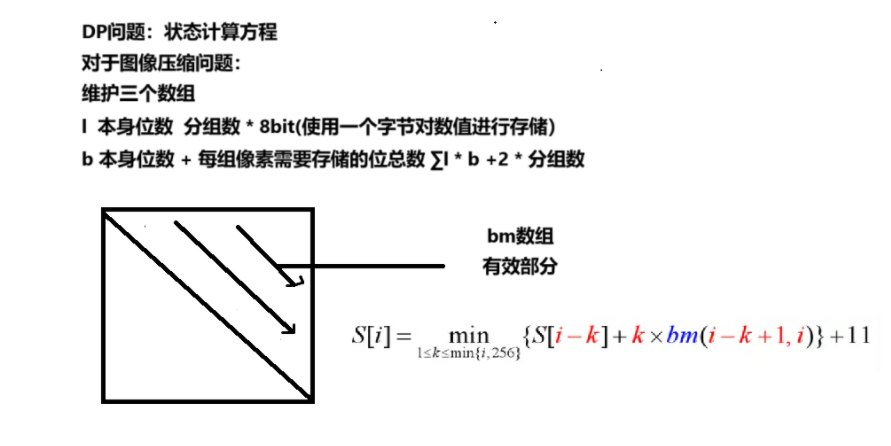
符号说明：

bm[i][j]: 表示从[i,j]区间内图像像素所需的最大表示位数
s[i]: [1,i]区间像素压缩之后的最小比特值
p[i]: 存储像素序号位i的所需的最小比特数
l[i]:存储当前像素需要之前的同一像素段的长度（包括i本身）
b[i]: 当前像素所处像素段的最小比特数

代码

#include<iostream>
#include<cmath>

using namespace std;    
const int N=110,M=11;   // 每个像素段需要使用额外的11bit存储段信息
int s[N],l[N],b[N],p[N];
int bm[N][N];   // bp[i,j] -> [i - j] 像素点编码长度最大值
int n;

int main(){
    cin >> n;
    for(int i=1;i<=n;i++){
        int x;
        scanf("%d",&x);
        p[i] = bm[i][i] = ceil(log2(x+1));  // 像素需要从1开始
    }
    // 初始化bm数组 (上三角部分有效)
    for(int l = 1;l <= n-1;l ++){
        for(int i = 1;i + l <= n;i ++){
            bm[i][i + l] = max(bm[i][i+l-1],p[i + l]);
        }        
    }
    // 更新s数组并维护
    for(int i=1;i<=n;i++){
        b[i] = p[i];
        l[i] = 1;   // 初始化新段的信息header =11;
        s[i]=s[i-1]+bm[i][i];
        for(int k=2 ; k<=i & k < 256;k ++){
            if(s[i] > s[i - k] + k * bm[i-k+1][i]){
                l[i] = k;
                b[i]=bm[i-k+1][i];
                s[i]=s[i - k] + k * bm[i-k+1][i];
            }
        }
        s[i]+=11;    // 3bit段像素长度和8bit长度信息
    }

    cout<<s[n]<<endl;
    // for(int i=1;i<=n;i++){
    //     cout<<l[i]<<" ";
    // }
    // cout<<endl;
    // for(int i=1;i<=n;i++){
    //     cout<<b[i]<<" ";
    // }
    // cout<<endl;
    int i=n;
    while(i > 0){
        cout << "("<<l[i]<<","<<b[i]<<")"<<" ";
        i -= l[i];
    }
    cout<<endl;
    return 0;
}

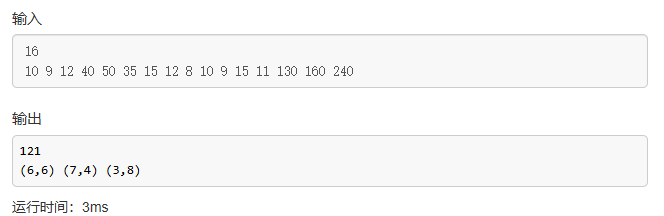
输入数据（复制用）

16
10 9 12 40 50 35 15 12 8 10 9 15 11 130 160 240

测试样例