seq2seq中的attention（一）

作者： 作者的头像   巷港 ,  2024-11-04 21:35:05 ,  所有人可见 ,  阅读 5

0


我们前面学习了seq2seq端到端思想的模型架构，解决了之前分模块优化的耦合问题。但seq2seq也有自己的问题。

我们不难发现，以机器翻译任务为例，encoder最终所有的信息都是集中在最后一个隐藏层，从而输出给decoder作为初始的输入。

但encoder通常是用rnn、lstm、gru等时序架构模型，就会存在梯度消失、信息丢失的问题。

对于较长的句子，我们很难寄希望于将输入的序列转化为定长的向量而保存所有的有效信息，所以随着所需翻译句子的长度的增加，这种结构的效果会显著下降。

那明确了问题，我们问一下自己想要实现什么呢？

  1. 既然原始输入的所有信息很难全部保留下来，那可以就不用全部保留嘛？
  2. 既然不全部保留，那我就得留下对翻译有用的重要信息。
  3. 我咋知道哪些信息对于翻译重要呢？decoder模型在预测每个词的时候，我可以知道重点关注encoder的哪些信息嘛？

感觉通透了很多。总结一下我们需要解决的：

在decoder的每一步，通过与encoder的直接关联来决定当前翻译应关注的源语句的重点部分。

由此，attention来啦！

attention，顾名思义就是注意力，其实参考的就是人类面对问题的思考思路。我们在翻译当前词语时，会去寻找源语句中相对应的几个词语，并结合之前的已经翻译的部分作出相应的翻译。

1.png

我们先直观的看一下attention的过程：

2.png

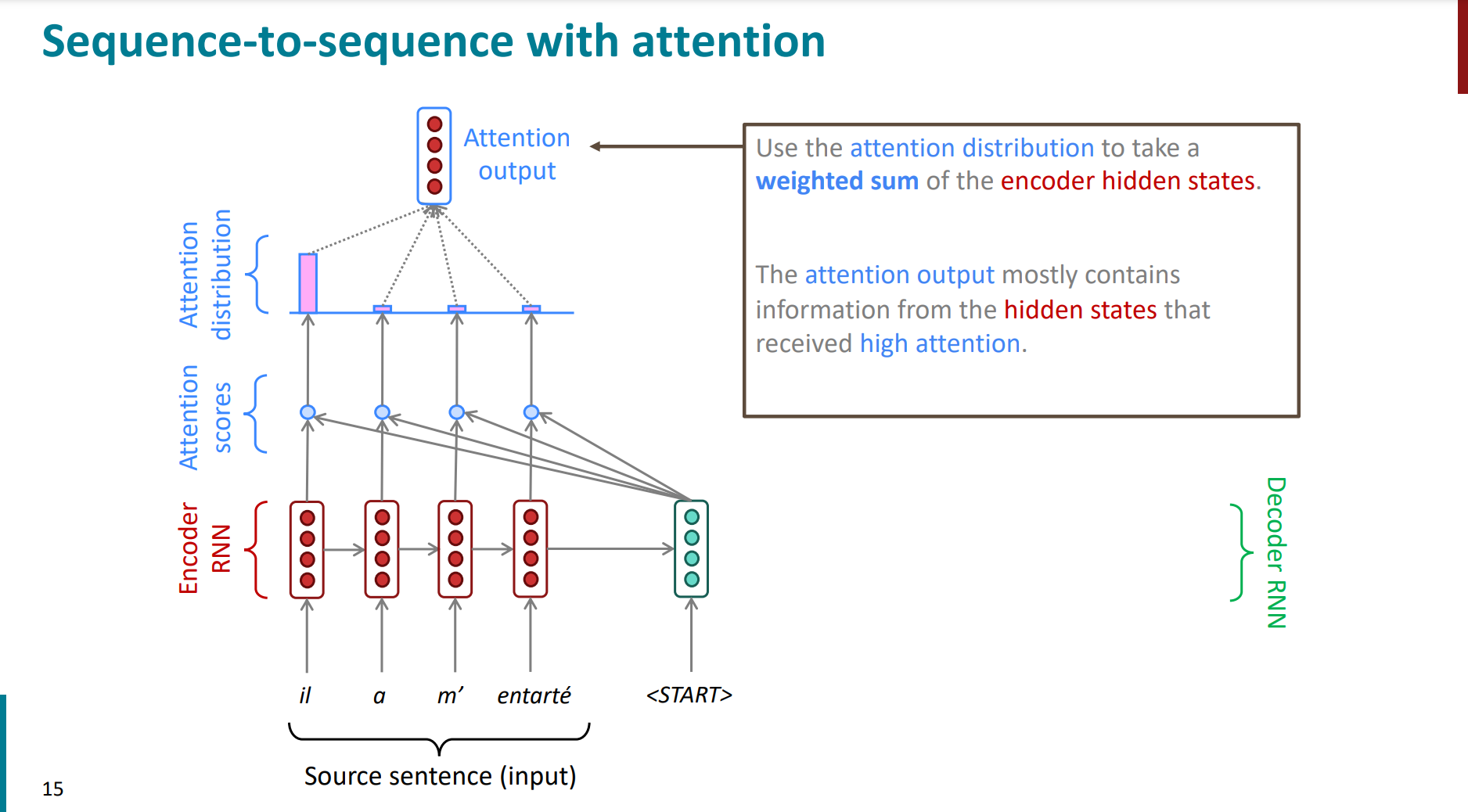
  1. 将decoder与encoder的每个位置做一个类似“点积”的运算
  2. 用softmax得出一个概率分布。
  3. 计算这些概率分布的一个加权得分，并与decoder当前的hidden states进行连接，从而完成当前词的预测结果。

接下来我们结合一下具体的数学符号表示进行attention计算过程的理解。

4.png

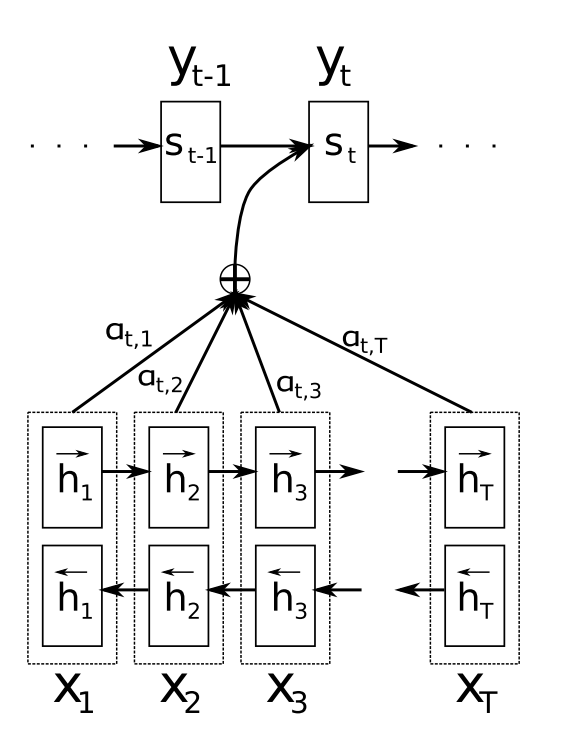
  1. 先拿到encoder的每个隐藏层信息$\textsf{hidden state }(h_1,h_2,\ldots,h_T)$
  2. 假设当前的decoder的隐藏层是$s_{t-1}$。那么就可以计算当前decoder与encoder的每个位置（即每个输入位置$j$与输出位置）的关联性（通常是点积）$e_{tj}=a(s_{t-1},h_j)$，有很多种计算方式（这不是重点）。
  3. 之后对这个关联性进行softmax处理，得到一个概率分布，即attention的分布情况$\overrightarrow{\alpha_t}=softmax(\overrightarrow{e_t})$
  4. 对概率分布进行加权求和，得到attention最终的得分$\overrightarrow{c_t}=\sum_{j=1}^T\alpha_{tj}h_j$。
  5. 这样我们就可以计算decoder的下一个hidden state$s_t=f(s_{t-1},y_{t-1},c_t)$
  6. 根据隐藏层的内容，我们就可以给出该位置预测的输出word：$p(y_t|y_1,\ldots,y_{t-1},\vec{x})=g(y_{i-1},s_i,c_i)$

3.png

这里关键的操作是计算encoder与decoder state之间的关联性的权重，得到Attention分布，从而对于当前输出位置得到比较重要的输入位置的权重，在预测输出时相应的会占较大的比重。

我们发现，attention引入前后最大的区别就是：纯seq2seq，decoder用的信息是ecoder的最后一个hidden state的单一最终向量，所有的信息都指望着浓缩在这个向量中；引入attention的话，我们可以每预测一个词，就去encoder中看看我们应该重点关注哪些信息，有了重点，而且没有丢失信息。

attention引入之后，模型的性能确实有了显著提升。而且因为有了这个注意力矩阵，让模型的可解释性也更强。

我们通过观察attention 权重矩阵的变化，可以更好地知道哪部分翻译对应哪部分源文字

5.png

接下来，我们简单回顾一下attention的关键参数和计算过程：

  1. encoder对应的values；decoder对应的query
  2. 计算attention得分（多种点积计算方法）
  3. 过一个softmax，得到attention的概率分布。
  4. 计算概率分布的加权得分，也叫做context vector

6.png

关于attention中关联性计算得分的方法，有很多种，常见的如下：

7.png

8.png

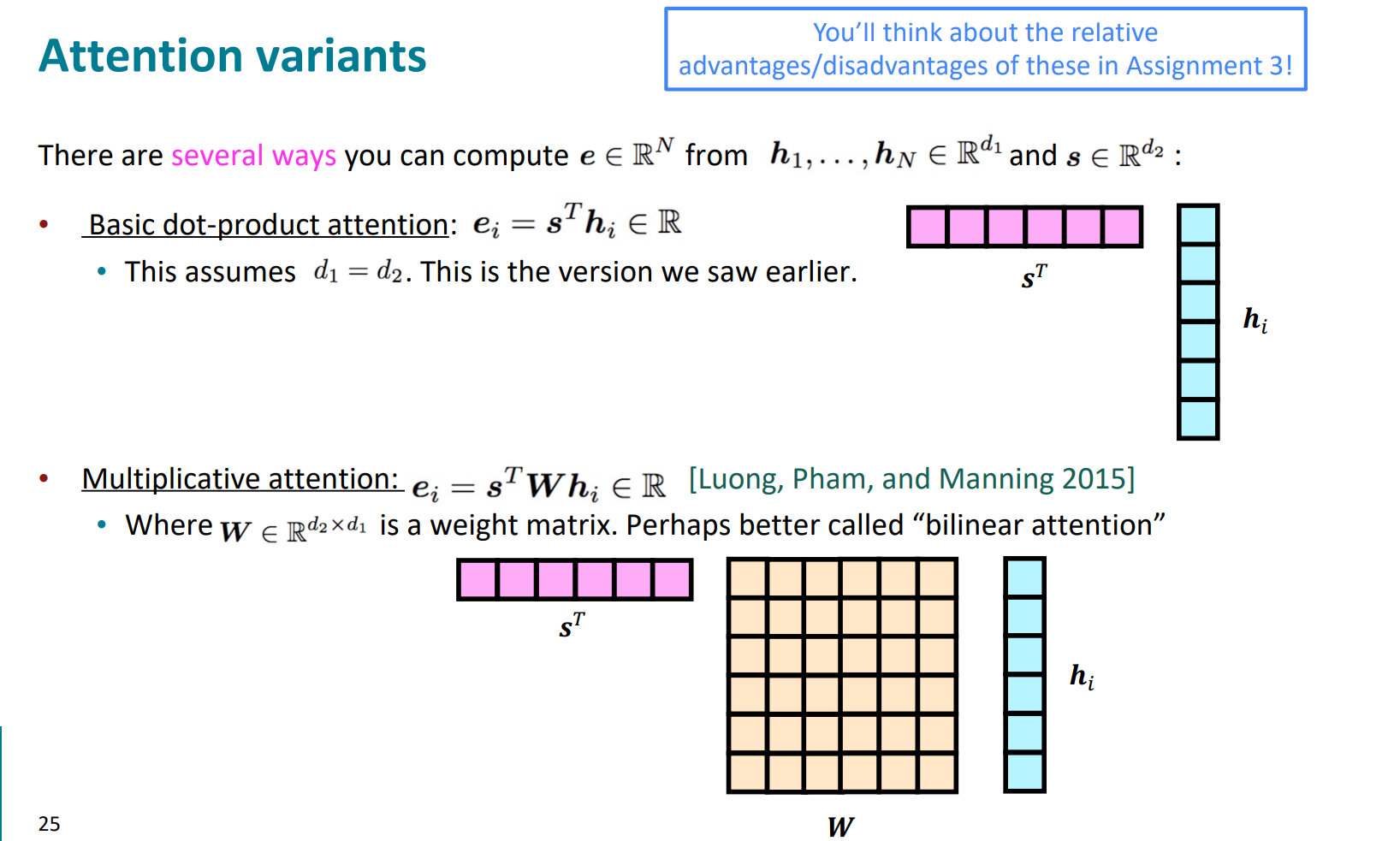
Reduced-rank multiplicative attention对应的$e_i=s^T(U^TV)h_i=(Us)^T(Vh_i)$就是transformer中的方法，我们之后重点去剖析。

attention的效果非常显著，当然也不局限于应用在seq2seq模型架构中。

standford也给出了一个更普适性的attention定义：

对于一个query和系列values，attention就能计算出针对当前query，这些values的一个加权求和的值，这个值代表了query认为这些values中应该重点关注哪些信息。

9.png

10.png

到此，我们就知道在以rnn为基础架构模型的seq2seq中，引入了attention之后的效果变化。

但我们到这里也许会有一个疑问：

这个rnn的架构真的还有必要存在嘛？因为attention本身就已经可以一边预测，一边看到全局信息了，而且rnn还不能并行操作。

我们之后就重点去学习transformer架构的attention机制。

参考致谢

https://web.stanford.edu/class/cs224n/slides/cs224n-spr2024-lecture07-final-project.pdf
https://zhuanlan.zhihu.com/p/47063917

0 评论