T1

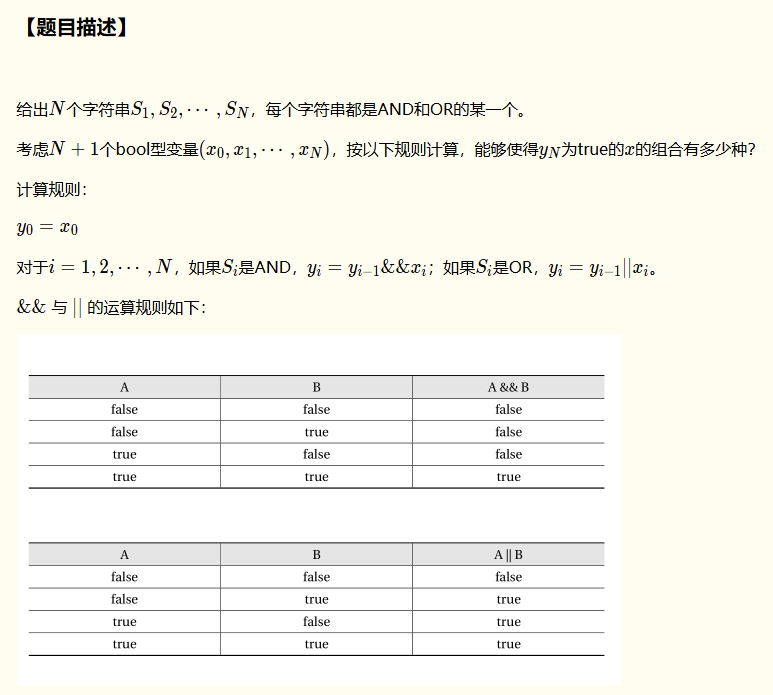
看完题目后发现如果暴力搜索会TLE($2^{60}$ 不爆炸才怪)
所以这道题可以想到用记忆化搜索或DP，其实这两种方法可以灵活运用，这里直讲思路
我们定义 count(p, st) 表示用从$x_1$到逻辑$x_p$得出的状态为st的方法数

count(p, st):
    if (st == 0)
        if (x[p] == AND)
        //有三种情况，分别是(Y, N), (N, Y), (N, N)
        //但是右边的情况不重要，因为右边只有一个值，你想给他定义什么就定义什么，不影响其他值
        // 所以我们只用关心让左边符合情况的方案数，就是count(p - 1, 0或1)
        // 左边有1个Y, 2个N
            return count(p - 1, 0) * 2 + count(p - 1, 1)
        if (x[p] == OR)
            // 只有一种情况，就是(N, N)，左边只有1个N
            return count(p - 1, 0)
    if (st == 1)
        // 同理，不过是反着来
        if (x[p] == AND)
            // (Y, Y), 1个Y
        if (x[p] == OR)
            // (Y, Y), (X, Y), (Y, X), 2个Y, 1个X

AC代码：

#include <bits/stdc++.h>
#define int long long
using namespace std;
string a[65];
typedef pair<int, int> PII;
map<PII, int> v;
int count(int p, int st) {
    if (v[{p, st}]) return v[{p, st}];
    if (p == 0) {
        v[{p, st}] = 1;
        return 1;
    }
    if (!st) {
        if (a[p] == "AND") {
            int num = 0;
            num = num + count(p - 1, 0) * 2;
            num = num + count(p - 1, 1);
            v[{p, st}] = num;
            return num;
        }
        if (a[p] == "OR") {
            int num = count(p - 1, 0);
            v[{p, st}] = num;
            return num;
        }
    }
    else {
        if (a[p] == "AND") {
            int num = count(p - 1, 1);
            v[{p, st}] = num;
            return num;
        }
        if (a[p] == "OR") {
            int num = 0;
            num = num + count(p - 1, 1) * 2;
            num = num + count(p - 1, 0);
            v[{p, st}] = num;
            return num;
        }
    }
}
signed main() {
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    cout << count(n, 1);
    return 0;
}

T2

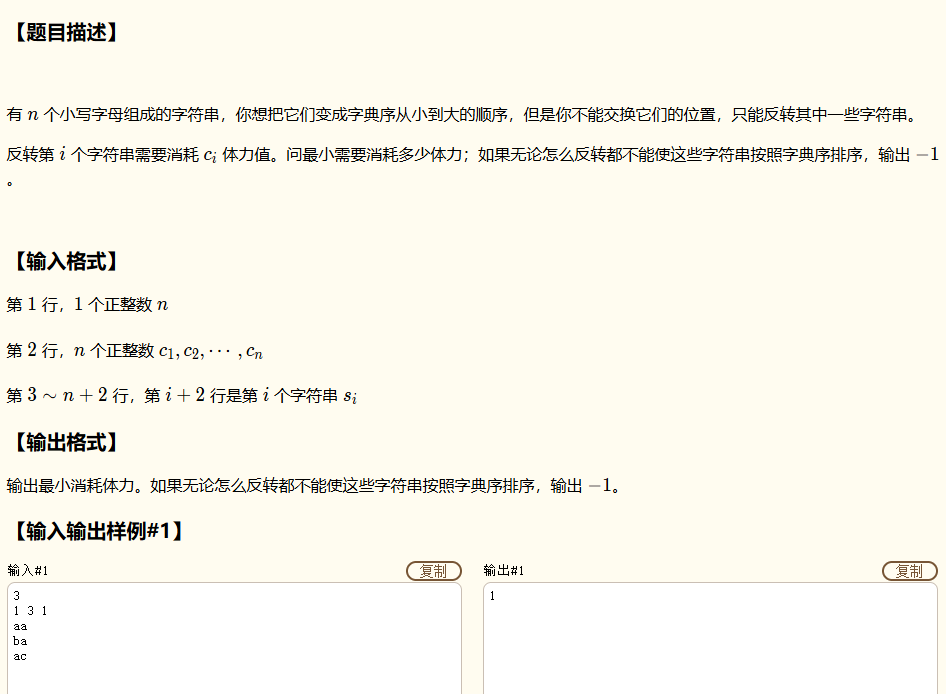
也是DP，但是先咕咕吧，到时候再写题解，这里先贴AC代码

#include <bits/stdc++.h>
#define int long long
using namespace std;
int c[100005], dp[100005][2];
string l[100005], r[100005];
signed main() {
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> c[i];
    for (int i = 1; i <= n; i++) cin >> l[i];
    for (int i = 1; i <= n; i++) r[i] = l[i], reverse(r[i].begin(), r[i].end());
    memset(dp, 0x3f, sizeof dp);
    dp[1][0] = 0; dp[1][1] = c[1];
    for (int i = 2; i <= n; i++) {
        if (l[i - 1] <= l[i]) dp[i][0] = min(dp[i][0], dp[i - 1][0]);
        if (r[i - 1] <= l[i]) dp[i][0] = min(dp[i][0], dp[i - 1][1]);
        if (l[i - 1] <= r[i]) dp[i][1] = min(dp[i][1], dp[i - 1][0] + c[i]);
        if (r[i - 1] <= r[i]) dp[i][1] = min(dp[i][1], dp[i - 1][1] + c[i]);
    }
    int ans = min(dp[n][0], dp[n][1]);
    if (ans < dp[0][0]) cout << ans << endl;
    else cout << -1 << endl;
    return 0;
}