3.2区间的维护和查询

连续和查询问题.给定一个n个元素的数组a1,a2,,,an,你的任务是设计一个数据结构,支持一个查询操作query(l,r)
来计算a[l]+a[l+1]+…+a[r],借助前缀和思想解决,只是如果加了个修改操作就得维护数组,这时候就需
要数据结构
了!!!

树状数组

数状数组注意:类似树,如图
lowbit(x)函数表示为x的二进制表示式中最右边的1所对应的值
灰色结点是BIT中的结点,(),每一层结点的lowbit相同,而且lowbit越大,越靠近根.图中的虚线是BIT中的边.注意编
号为0的点是虚拟结点,它并不是树的一部分,(所以树状数组的下标一定是从1开始).
C数组的表达式为C[i]=A[i-lowbit(i)+1]+A[i-lowbit(i)+2]+…A[i];
换句话说C的每个元素都是A数组中的一段连续和.

经典应用
a:求序列中满足三个数字单调递增,单调递减的组数，或者V型和^型的组数;
楼兰图腾
乒乓比赛
b.区间修改或单点修改和查询区间和

RMQ

RMQ求的是一类区间最值的问题
优点:好写 缺点:不支持修改
一道巧妙的RMQ问题
求解一个区间中连续出现次数最多的数出现的次数
频繁出现的数值
这题的题解很巧妙的化为一个RMQ问题,见下图:

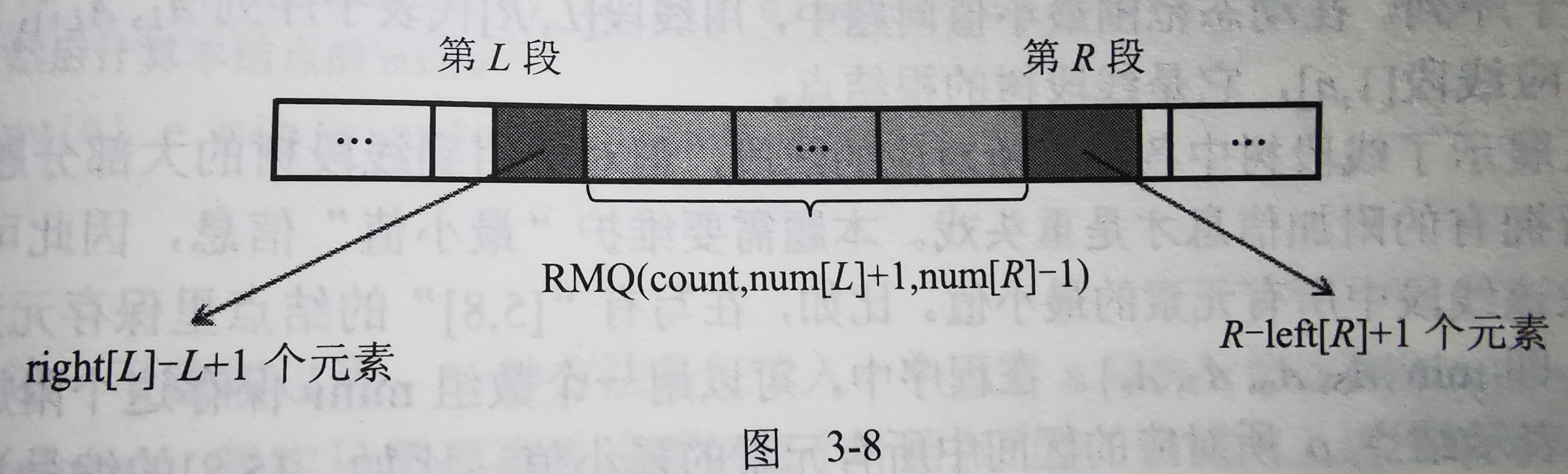
区间是[l,r]!!

首先把a数组划分为cnt段,这cnt段中的所有数都是相同的
用l数组表示某个段中的左端点,r数组表示某个段中的右端点,num记录段的编号
然后区间被划分为三个部分
a.包含l的段num[l]
b.包含r的段num[r]
c.区间中的其它段
这里还有一些分段的特殊情况(接下来会分析)
然后便是上面的图
首先l所在段的频繁出现的次数是r[num[l]]-l+1,
r所在段的频繁出现次数是r-l[num[r]]+1;
中间所在段就可以用rmq来直接求出最大的频繁出现次数!!这个转化真的难qwq
算法流程
f[i][j]表示从i段开始跳$2^j$步所到达的段的频繁出现次数
(1) 预处理出所有num,l,r数组
(2) st表
(3)查询
细节
注意
a.l和r可能处于一个段;
b.l,r可能处于相邻段,不需要rmq;

代码

#include<bits/stdc++.h>
using namespace std;
#define read(x) scanf("%d",&x)
const int N =500010;
int num[N],l[N],r[N];
int f[N][20],n,cnt,m;
void my_clear()
{
    cnt=0;
    memset(l,0,sizeof l);
    memset(r,0,sizeof r);
    memset(f,0,sizeof f);
    memset(num,0,sizeof num);
}
int main()
{
    while(1)
    {
        my_clear();
        read(n);
        if(!n) break;
        read(m);
        int tmp=-2e9;
        for(int i=1;i<=n;i++)
        {   
            int x;
            read(x);
            if(x!=tmp)  r[cnt]=i-1,l[++cnt]=i,tmp=x;//段的左右端点l,r
            //端中的值tmp
            num[i]=cnt;//第i个位置的值在第cnt段
        }

    for(int j=0;(1<<j)<=cnt;j++)//
        for(int i=1;i+(1<<j)-1<=cnt;i++)//i表示起点
        {
            if(!j)  f[i][0]=r[i]-l[i]+1;//预处理f数组
            else    f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
        }

    for(int i=1;i<=m;i++)
    {
        int x,y;
        read(x),read(y);
        if(x>y) swap(x,y);
        if(num[x]==num[y])  printf("%d\n",y-x+1);
        else
        {
            int ans=0;
            if(num[x]+1<=num[y]-1)//这句话很重要
            {
                int ls=num[x]+1,rs=num[y]-1;
                int ll=log(rs-ls+1)/log(2);

                ans=max(f[ls][ll],f[rs-(1<<ll)+1][ll]);
            }
            ans=max(ans,max(r[num[x]]-x+1,y-l[num[y]]+1));
            printf("%d\n",ans);
        }
    }
    }
}

相似题 连续不同的数的最大长度(与众不同)

线段树

主要是单点修改和区间修改
这里就不作赘述了
这里补充一种特殊的信息维护
将区间所有值都设定为同一个值setv
注意这种标记是直接修改为另一个值,而不是想addv一样加上一个值
需要在传标记的时候把原标记直接写成新的标记,然后传到左右儿子,最后清空就好
当我一个子区间中有addv标记和setv标记时,必须优先执行setv标记,因为一旦有setv标记,
原来的addv就清零了!!!(更具体一点,假设setv先传进来,那没啥问题,但setv后传进来,那addv是不是就废了hh,综上所述
setv是优先的)
二维线段树
用二维线段树维护矩阵(当矩阵不大时)r行c列
思路:
每一行都建立一棵线段树,这样就有r棵线段树
然后比如对(x1,y),(x2,y2)子矩阵进行修改只需要枚举x1~x2行,对每一列的y1~y2区间进行修改就好

题目 矩阵修改

对矩阵有两个信息需要维护
a:将(x1,y1,x2,y2)子矩阵全部设置为setv
b:将(x1,y1,x2,y2)子矩阵全部加上为addv
c:询问子矩阵最大值 最小值 和

代码

#include<bits/stdc++.h>
using namespace std;
const int N= 1000005, INF = 0x3f3f3f3f; // -1u/2=INT_MAX

struct Tr{
    struct node {
        int l,r;
        int sumv, maxv, minv;
        int addv, setv;//和标记和设置标记
    };
    node tr[N*4];
    void build(int u, int l, int r)
    {
        tr[u]={l,r,0,0,0,0,-1};
        if (l == r) return;
        int mid=l+r>>1;
        build(u<<1,l,mid),build(u<<1|1,mid+1,r);
    }
    void pushup(int u)
    {
        tr[u].sumv = tr[u<<1].sumv + tr[u<<1|1].sumv;
        tr[u].maxv = max(tr[u<<1].maxv, tr[u<<1|1].maxv);
        tr[u].minv = min(tr[u<<1].minv, tr[u<<1|1].minv);
    }
    void pushdown(int u)
    { // 若setv与addv同时有效，必然set操作在前，因为在set操作时已将addv置0
      //记住就好
        int l=tr[u].l,r=tr[u].r;
        int mid = (l + r) >> 1;
        if (tr[u].setv >= 0) {
            tr[u<<1].setv = tr[u<<1|1].setv = tr[u].setv;
            tr[u<<1].addv = tr[u<<1|1].addv =0; // 处理setv时要将左右儿子addv清零。
            tr[u<<1].sumv = (mid - l + 1) * tr[u].setv;
            tr[u<<1|1].sumv = (r - mid) * tr[u].setv;
            tr[u<<1].minv = tr[u<<1].maxv = tr[u<<1|1].minv = tr[u<<1|1].maxv = tr[u].setv;
            tr[u].setv = -1; // 标记置0
        } // 先处理setv
        if (tr[u].addv) {
            tr[u<<1].addv += tr[u].addv;
            tr[u<<1|1].addv += tr[u].addv;
            tr[u<<1].sumv += (mid - l + 1) * tr[u].addv;
            tr[u<<1|1].sumv += (r - mid) * tr[u].addv;
            tr[u<<1].minv += tr[u].addv;
            tr[u<<1].maxv += tr[u].addv;
            tr[u<<1|1].minv += tr[u].addv;
            tr[u<<1|1].maxv += tr[u].addv;
            tr[u].addv = 0; // 标记置0
        }
    }
    void modify1(int u,int l, int r, int v) // add操作
    {
        if (l <= tr[u].l && tr[u].r<= r) { // setv不变
            tr[u].addv += v;
            tr[u].sumv += (tr[u].r - tr[u].l + 1) * v;
            tr[u].minv += v;
            tr[u].maxv += v;
            return;
        }
        pushdown(u);
        int mid= (tr[u].l+ tr[u].r) >> 1;
        if (l<= mid)
            modify1(u<<1,l,r,v);
        if (r> mid)
            modify1(u<<1|1,l,r,v);
        pushup(u);
    }
    void modify2(int u, int l, int r,int v) // set操作
    {
        if (l<= tr[u].l && r >= tr[u].r) {
            tr[u].addv = 0; // 将addv置0
            tr[u].setv = v;
            tr[u].sumv = (tr[u].r - tr[u].l + 1) * v;
            tr[u].minv = tr[u].maxv = v;
            return;
        }
        pushdown(u);
        int mid = (tr[u].l +tr[u].r) >> 1;
        if (l<= mid)
            modify2(u<<1,l,r,v);
        if (r> mid)
            modify2(u<<1|1,l,r,v);
        pushup(u);
    }
     node query(int u, int l, int r)
    {
        if (tr[u].l>= l && tr[u].r <=r)
            return tr[u];
        pushdown(u);
        int mid= (tr[u].l+tr[u].r)>> 1;
        if(l>mid)  return query(u<<1|1,l,r);
        else if(r<=mid)   return query(u<<1,l,r);
        else
        {
            node ans;
            auto ans1=query(u<<1,l,r);
            auto ans2=query(u<<1|1,l,r);
            ans.sumv=ans1.sumv+ans2.sumv;
            ans.maxv=max(ans1.maxv,ans2.maxv);
            ans.minv=min(ans1.minv,ans2.minv);
            return ans;
        }
    }
};

int main()
{
    int r, c, m;
    while (~scanf("%d%d%d", &r, &c, &m)) {
        Tr* tr= new Tr[r + 1]; // 动态开内存(tree[0]~tree[r])
        for (int i = 1; i <= r; i++)
            tr[i].build(1, 1, c); // 建树
        while (m--) {
            int opt, x1, y1, x2, y2, v;
            scanf("%d%d%d%d%d", &opt, &x1, &y1, &x2, &y2);
            if (opt == 1) {
                scanf("%d", &v);
                for (int i = x1; i <= x2; i++)
                    tr[i].modify1(1,y1,y2,v);
            } else if (opt == 2) {
                scanf("%d", &v);
                for (int i = x1; i <= x2; i++)
                    tr[i].modify2(1,y1,y2,v);
            } else {
                int sum = 0, minn = INF, maxx = -INF;
                for (int i = x1; i <= x2; i++) {
                    auto ans = tr[i].query(1,y1, y2);//对每一行进行询问
                    sum += ans.sumv;
                    minn = min(minn, ans.minv);
                    maxx = max(maxx, ans.maxv);
                }
                printf("%d %d %d\n", sum, minn, maxx);
            }
        }
        delete[] tr; // 释放内存
    }
    return 0;
}