概述
现在我们要解决一些图论问题,例如我们要解决一个将一个1616的正方形逐步划分为4个22的小正方形,然后去填色的问题!!
对于这个问题一般我们把他归结为模拟题,但是用数组去实现需要大量的空间,所以我们这里去用二叉树去解决,或者用四叉树去解决!!(这个就看自己的能力了),所以下面我们来看一下二叉树的简单知识点!
二叉树及其实现
定义(图论):
二叉树是一个连通的无环图,并且每一个顶点的度不大于3。有根二叉树还要满足根节点的度不大于2。有了根节点之后,每个顶点定义了唯一的父节点,和最多2个子节点。然而,没有足够的信息来区分左节点和右节点。如果不考虑连通性,允许图中有多个连通分量,这样的结构叫做森林。
几种特殊的二叉树
- 斜树
所有结点都只有左子树的二叉树叫左斜树,所有结点都只有右子树的二叉树叫右斜树。斜树的每一层都只有一个结点,结点的个数与斜树的深度相同。- 满二叉树
在一棵二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子结点都在同一层上,这样的二叉树称为满二叉树。(上图中所示的二叉树,就是一棵满二叉树)- 完全二叉树
对一棵具有n个结点的二叉树按层序编号,如果编号为i(1≤i≤n)的结点与同样深度的满二叉树中的编号为i的结点在二叉树中的位置完全相同,则这棵二叉树称为完全二叉树。
二叉树的性质
性质1 在二叉树的第i层上,至多有 2^(i-1)个节点(根节点的层数为1 )
性质2 深度为k的二叉树至多有 2^k-1个节点(k >=1)
性质3 一棵二叉树的叶子结点数为n0,度为2的结点数为n2,则n0 = n2 + 1
性质4 具有n个结点的完全二叉树的深度为floor(log2n) + 1
性质5 如果对一棵有n个结点的完全二叉树(其深度为floor(log2n) + 1 )的结点按层序编号,则对任一结点i(1≤i≤n)有:
(1) 如果i = 1,则结点i是二叉树的根,无双亲;如果i > 1,则其双亲PARENT(i)是结点 floor((i)/2)
(2)如果2i > n,则结点i无左孩子;否则其左孩子LCHILD(i)是结点2i
(3)如果2i + 1 > n,则结点i无右孩子;否则其右孩子RCHILD(i)是结点2i + 1
二叉树通常作为数据结构应用,典型用法是对节点定义一个标记函数,将一些值与每个节点相关系。这样标记的二叉树就可以实现二叉搜索树和二叉堆,并应用于高效率的搜索和排序。
注意:这里有一个小的知识点 就是取整函数
ceil(x)返回不小于x的最小整数值(然后转换为double型)。
floor(x)返回不大于x的最大整数值。
round(x)返回x的四舍五入整数值。
#include <math.h>
double ceil(double x);
double floor(double x);
double round(double x);
二叉树的存储
二叉树可以用数组或链接串列来存储,若是满二叉树就能紧凑排列而不浪费空间。如果某个节点的索引为i,(假设根节点的索引为0)则在它左子节点的索引会是2i+1,以及右子节点会是2i+2;而它的父节点(如果有)索引则为[(i-1)/2]。这种方法更有利于紧凑存储和更好的访问的局部性,特别是在前序遍历中。然而,它需要连续的存储空间,这样在存储高度为h的n个节点所组成的一般树时,将浪费很多空间。在最糟糕的情况下,如果深度为h的二叉树其每个节点都只有右孩子,则该存储结构需要占2^h-1用的空间,实际上却有h个节点,浪费了不少空间,是顺序存储结构的一大缺点。
二叉树的基本实现
- 顺序存储结构
/* 二叉树的顺序存储表示 */
#define MAX_TREE_SIZE 100 /* 二叉树的最大节点数 */
typedef TElemType SqBiTree[MAX_TREE_SIZE]; /* 0号单元存储根节点 */
typedef struct
{
int level,order; /* 即节点的层(按[满二叉树]计算) */
}position;
- 链式存储结构
/* 二叉树的二叉联表存储表示 */
typedef struct BiTNode
{
TElemType data;
struct BiTNode *lchild,*rchild; /* 左右儿子指針 */
}BiTNode,*BiTree;
/* 二叉树的三叉链表存储表示 */
typedef struct BiTPNode
{
TElemType data;
struct BiTPNode *parent,*lchild,*rchild; /* 父、左右儿子指針 */
}BiTPNode,*BiPTree;
- 基本实现
//二叉树 节点结构
template<class T>
struct BinaryTreeNode
{
typedef BinaryTreeNode<T>* Treepoint ;
BinaryTreeNode(const T& data)
:_data(data)
, pLeft(NULL)
, pRight(NULL)
{}
T _data;
Treepoint pLeft;
Treepoint pRight;
};
//二叉树的基本操作
template<class T>
class BinaryTree
{
public:
BinaryTree()
:_pRoot(NULL)
{}
BinaryTree(T arr[], size_t sz)
{
size_t index = 0;
_CreatNode(_pRoot, arr, sz, index);
}
BinaryTree(const BinaryTree<T>& t)//拷贝构造
{
_pRoot = _CopyTree(t._pRoot);
}
BinaryTreeNode<T>& operator=(const BinaryTree<T>& t) //赋值运算符重载
{
if (this != &t)
{
_Destroy(this->_pRoot);
this->_pRoot = _CopyTree(t._pRoot);
}
return *this;
}
~BinaryTree() //析构函数
{
if (this != NULL)
{
_Destroy(this->_pRoot);
}
}
private:
BinaryTreeNode<T>* _pRoot;
protected:
void _CreatNode(BinaryTreeNode<T>*& Root, T arr[], size_t sz, size_t& index)//创建
{ //传的是引用 //引用
if (index < sz && arr[index] != '?')
{
//前序遍历 :创建过程 根-左-右
Root = new BinaryTreeNode<T>(arr[index]);
_CreatNode(Root->pLeft, arr, sz, ++index);
_CreatNode(Root->pRight, arr, sz, ++index);
}
}
BinaryTreeNode<T>* _CopyTree(const BinaryTreeNode<T>* Root) //拷贝
{
BinaryTreeNode<T>* NewRoot = NULL;
if (Root != NULL)
{
NewRoot = new BinaryTreeNode<T>(Root->_data);
NewRoot->pLeft = _CopyTree(Root->pLeft);
NewRoot->pRight = _CopyTree(Root->pRight);
}
return NewRoot;
}
void _Destroy(BinaryTreeNode<T>*& Root) //删除顺序 左-右-根
{
if (Root != NULL)
{
_Destroy(Root->pLeft);
_Destroy(Root->pRight);
// _Destroy(Root);
delete Root;
Root = NULL;
}
}
};
二叉树的遍历
二叉树的遍历本质上就是出栈和入栈的过程。遍历的递归方式简单又容易理解,但是效率始终是个问题。
非递归算法可以清楚地知道遍历的每一个细节,但是就不容易理解。
遍历即将树的所有结点访问且仅访问一次。按照根节点位置的不同分为前序遍历,中序遍历,后序遍历。
前序遍历:根节点->左子树->右子树
中序遍历:左子树->根节点->右子树
后序遍历:左子树->右子树->根节点
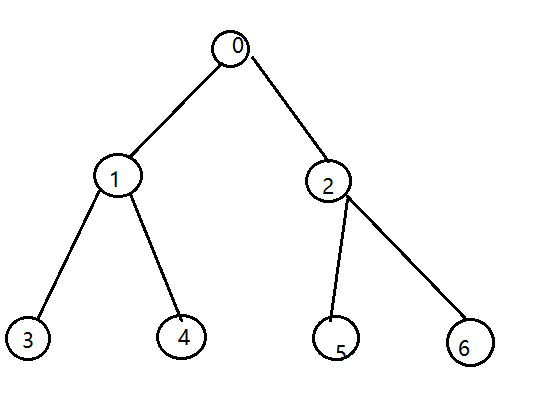
前序遍历:0 134 256
中序遍历:314 0 526
后序遍历:341 562 0
前序 中序 后序遍历
遍历二叉树:L、D、R分别表示遍历左子树、访问根结点和遍历右子树,则先(根)序遍历二叉树的顺序是DLR,中(根)序遍历二叉树的顺序是LDR,后(根)序遍历二叉树的顺序是LRD。还有按层遍历二叉树。这些方法的时间复杂度都是O(n),n为结点个数。
如果T2是由有序树T转换而来的二叉树,那么T中结点的前序就是T2中结点的前序,T中结点的后序就是T2中结点的中序。任何一棵二叉树的叶结点在先序、中序和后序遍历中的相对次序不发改变。设n,m为一棵二叉树上的两个结点,在中序遍历时,n在m前的条件是n在m的左方。前序序列和中序序列相同的二叉树为空树或任一结点均无左孩子的非空二叉树;中序序列和后序序列相同的二叉树为空树或任一结点均无右孩子的非空二叉树;前序序列和后序序列相同的二叉树为空树或仅有一个结点的二叉树。
(简单来说就是访问时是叶节点的访问先后问题)
递归实现
假设我们有一个包含值的data和指向两个子结点的left和right的树结点结构。我们可以写出这样的过程:
void InorderTraversal( BinTree BT )
{
if( BT ) {
InorderTraversal( BT->Left );
/* 此处假设对BT结点的访问就是打印数据 */
printf("%d ", BT->Data); /* 假设数据为整型 */
InorderTraversal( BT->Right );
}
}
这样会用前序打印出树中的值。在前序,每个结点在访问它的子结点之前访问。类似地,如果打印语句在最后,每个结点在访问他的子节点之后访问,树中的值会用后序来打印。在这两种情况中,左子树中的值比右子树中得值先打印。
void PreorderTraversal( BinTree BT )
{
if( BT ) {
printf("%d ", BT->Data );
PreorderTraversal( BT->Left );
PreorderTraversal( BT->Right );
}
}
最后,上面的中序遍历,每个结点在访问左子树和右子树之间访问。这在遍历二叉搜索树时很常用,因为它能用递增的顺序来遍历所有的值。
为什么呢?如果n是二叉搜索树的结点,那么n的左子树的所有结点的值都比n的值要小,而且n的右子树的所有节点的值都比n的值要大。因此,如果我们顺序遍历左子树,然后访问n,然后顺序遍历右子树。我们就已经循序访问了整个树。
后序遍历伪代码如下:
void PostorderTraversal( BinTree BT )
{
if( BT ) {
PostorderTraversal( BT->Left );
PostorderTraversal( BT->Right );
printf("%d ", BT->Data);
}
}
非递归实现
以上的递归算法使用与树的高度成比例的栈空间。如果我们在每个结点中存储指向父结点的指针,那样可以使用反复运算算法,只使用常量空间实现所有这些遍历。然而,指向父结点的指针占用更前序遍历的反复运算算法:
void LevelorderTraversal ( BinTree BT )
{
Queue Q;
BinTree T;
if ( !BT ) return; /* 若是空树则直接返回 */
Q = CreatQueue(); /* 创建空队列Q */
AddQ( Q, BT );
while ( !IsEmpty(Q) ) {
T = DeleteQ( Q );
printf("%d ", T->Data); /* 访问取出队列的结点 */
if ( T->Left ) AddQ( Q, T->Left );
if ( T->Right ) AddQ( Q, T->Right );
}
}
其他的类似!!!
相关运用
输出叶子节点
void PerOrderPintLeaves(BinTree BT){
if(BT){
if(!BT->Left&&!BT->Right)cout<<BT->Data<<endl;
PerOrderPintLeaves(BT->Left);
PerOrderPintLeaves(BT->Right);
}
}
二叉树的高度
void PerOrderPintLeaves(BinTree BT){
int HL,HR,MaxH;
if(BT){
HL=PerOrderPintLeaves(BT->Left);
HR=PerOrderPintLeaves(BT->Right);
MaxH=(HL>HR)?HL:HR;
return (MaxH+1);
}
else return 0;
}
还有的遍历就是DFS与BFS 打开学习的大门
二叉搜索树(查找树)
就是一个二分法的运用!!所以我们不做过多的介绍:
//递归查找
BinTree Find( BinTree BST, ElementType X ){
if(!BST)return NULL;
if(X>BST->Data)return Find(X,BST->Right);
else if(x<BSt->Data)return Find(X,BST->Left);
else return BST;
}
//非递归查找
BinTree IterFind( BinTree BST, ElementType X ){
while(BST){
if(X>BST->Data)return Find(X,BST->Right);
else if(x<BSt->Data)return Find(X,BST->Left);
else return BST;
}
return NULL;
}
//找最小值
Position FindMin(BinTree BST){
if(!BST)return NULL:
else if(!BST->Left)return BST;
else return FindMin(BST->Left);
}
//找最大值
Position FindMax(BinTree BST){
if(!BST)while(BST->Right)BST=BST->Right;
return BST;
}
BinTree Insert( BinTree BST, ElementType X )
{
if( !BST ){ /* 若原树为空,生成并返回一个结点的二叉搜索树 */
BST = (BinTree)malloc(sizeof(struct TNode));
BST->Data = X;
BST->Left = BST->Right = NULL;
}
else { /* 开始找要插入元素的位置 */
if( X < BST->Data )
BST->Left = Insert( BST->Left, X ); /*递归插入左子树*/
else if( X > BST->Data )
BST->Right = Insert( BST->Right, X ); /*递归插入右子树*/
/* else X已经存在,什么都不做 */
}
return BST;
}
BinTree Delete( BinTree BST, ElementType X )
{
Position Tmp;
if( !BST )
printf("要删除的元素未找到");
else {
if( X < BST->Data )
BST->Left = Delete( BST->Left, X ); /* 从左子树递归删除 */
else if( X > BST->Data )
BST->Right = Delete( BST->Right, X ); /* 从右子树递归删除 */
else { /* BST就是要删除的结点 */
/* 如果被删除结点有左右两个子结点 */
if( BST->Left && BST->Right ) {
/* 从右子树中找最小的元素填充删除结点 */
Tmp = FindMin( BST->Right );
BST->Data = Tmp->Data;
/* 从右子树中删除最小元素 */
BST->Right = Delete( BST->Right, BST->Data );
}
else { /* 被删除结点有一个或无子结点 */
Tmp = BST;
if( !BST->Left ) /* 只有右孩子或无子结点 */
BST = BST->Right;
else /* 只有左孩子 */
BST = BST->Left;
free( Tmp );
}
}
}
return BST;
}
二叉树的线索化及其遍历
二叉树的线索化定义
线索二叉树(英语:threaded binary tree,保留遍历时结点在任一序列的前驱和后继的信息):若结点有左子树,则其lchild域指示其左孩子,否则令lchild域指示其前驱;若结点有右子树,则其rchild域指示其右孩子,否则令rchild指示其后继。还需在结点结构中增加两个标志域LTag和RTag。LTag=0时,lchild域指示结点的左孩子,LTag=1时,lchild域指示结点的前驱;RTag=0时,rchild域指示结点的右孩子,RTag=1时,rchild域指示结点的后继。以这种结点结构构成的二叉链表作为二叉树的存储结构,叫做线索链表,其中指向结点前驱和后继的指针叫做线索,加上线索的二叉树称为线索二叉树。对二叉树以某种次序遍历使其变为线索二叉树的过程叫做线索化。若对二叉树进行中序遍历,则所得的线索二叉树称为中序线索二叉树,线索链表称为为中序线索链表。线索二叉树是一种物理结构。
首先对于左子树存在的节点,就不会有前驱;同样,节点的右子树存在,那么不存在后继。那么我就先一直找寻节的左子树,判断左右子树是否为空 , 为空了才会考虑前驱和后继的问题。后继倒是很好找(反正要遍历二叉树),那么前驱的位置呢?如果遇到左子树不存在的节点,怎么才能找到已经已经扫面过得节点呢?所以我们需要创建一个节点指针,每次记住上一次扫描的节点 。 对于右子树就很好办了,如果当前节点的前一个节点不为空且右子树不存在,那么我们就放心大胆的链上吧 。然后循环得了。
个人简化版本:
n个结点的二叉链表中含有n+1个空指针域。利用二叉链表中的空指针域,存放指向结点在某种遍历次序下的前趋和后继结点的指针(这种附加的指针称为”线索”)。
这种加上了线索的二叉链表称为线索链表,相应的二叉树称为线索二叉树(Threaded BinaryTree)。根据线索性质的不同,线索二叉树可分为前序线索二叉树、中序线索二叉树和后序线索二叉树三种。
注意:
线索链表解决了二叉链表找左、右孩子困难的问题,出现了无法直接找到该结点在某种遍历序列中的前趋和后继结点的问题。
/* 二叉树的二叉线索存储表示 */
typedef enum{
Link,Thread
}PointerTag; /* Link(0):指针,Thread(1):线索 */
typedef struct BiThrNode
{
TElemType data;
struct BiThrNode *lchild,*rchild; /* 左右儿子指针 */
PointerTag LTag,RTag; /* 左右标志 */
// ltag和rtag是增加的两个标志域,用来区分结点的左、右指针域是指向其左、右孩子的指针,还是指向其前趋或后继的线索。
}BiThrNode,*BiThrTree;
二叉树转中序线索化
算法与中序遍历算法类似。只需要将遍历算法中访问结点的操作具体化为建立正在访问的结点与其非空中序前趋结点间线索。
该算法应附设一个指针pre始终指向刚刚访问过的结点(pre的初值应为NULL),而指针p指示当前正在访问的结点。结点pre是结点p的前趋,而p是pre的后继。
和中序遍历算法一样,递归过程中对每结点仅做一次访问。因此对于n个结点的二叉树,算法的时间复杂度亦为O(n)。
typedef enum { Link,Thread} PointerTag; //枚举值Link和Thread分别为0,1
typedef struct node{
DataType data;
PointerTag ltag,rtag; //左右标志
Struct node *lchild,*rchild;
} BinThrNode;\\线索二叉树的结点类型
typedef BinThrNode *BinThrTree;
BinThrNode *pre=NULL; //全局量
void lnorderThreading(BinThrTree p)
{//将二叉树p中序线索化
if(p){ //p非空时,当前访问结点是*p
InorderThreading(p->lchild); //左子树线索化
//以下直至右子树线索化之前相当于遍历算法中访问结点的操作
p->ltag=(p->lchild)?Link:Thread; //左指针非空时左标志为Link
//(即0),否则为Thread(即1)
p->rtag=(p->rchild)?Link:Thread;
*(pre){ //若*p的前趋*pre存在
if(pre->rtag==Thread) //若*p的前趋右标志为线索
pre->rchild=p; //令*pre的右线索指向中序后继
if(p->ltag==Thread) //*p的左标志为线索
p->lchild=pre; //令*p的左线索指向中序前趋
} // 完成处理*pre的线索
pre=p; //令pre是下一访问结点的中序前趋
InorderThreeding(p->rehild); //右子树线索化
}//endif
} //InorderThreading
线索化二叉树及遍历
- 无头指针
void InThreading(BiThrTree B,BiThrTree *pre) {
if(!B) return;
InThreading(B->lchild,pre);
if(!B->lchild){ //没有左孩子
B->LTag = Thread; //修改标志域为前驱线索
B->lchild = *pre; //左孩子指向前驱结点
}
if(!(*pre)->rchild){ //没有右孩子
(*pre)->RTag = Thread; //修改标志域为后继线索
(*pre)->rchild = B; //前驱右孩子指向当前结点
}
*pre = B; //保持pre指向p的前驱
InThreading(B->rchild,pre);
}
- 有头指针
在线索二叉链表上添加一个head结点,并令其lchild域的指针指向二叉树的根结点(A),其rchild域的指针指向中序遍历访问的最后一个结点。同样地,二叉树中序序列的第一个结点中,lchild域指针指向头结点,中序序列的最后一个结点rchild域指针也指向头结点。
于是从头结点开始,我们既可以从第一个结点顺后继结点遍历,也可以从最后一个结点起顺前驱遍历。就和双链表一样。
//为线索二叉树添加头结点,使之可以双向操作
Status InOrderThreading(BiThrTree *Thrt,BiThrTree T){
if(!(*Thrt = (BiThrTree)malloc(sizeof(BiThrNode)))) exit(OVERFLOW); //开辟结点
(*Thrt)->LTag = Link;
(*Thrt)->RTag = Thread; //设置标志域
(*Thrt)->rchild = (*Thrt); //右结点指向本身
if(!T) {
(*Thrt)->lchild = (*Thrt);
return OK; //若根结点不存在,则该二叉树为空,让该头结点指向自身.
}
BiThrTree pre; //设置前驱结点
//令头结点的左指针指向根结点
pre = (*Thrt);
(*Thrt)->lchild = T;
//开始递归输入线索化
InThreading(T,&pre);
//此时结束了最后一个结点的线索化了,下面的代码把头结点的后继指向了最后一个结点.
//并把最后一个结点的后继也指向头结点,此时树成为了一个类似双向链表的循环.
pre->rchild = *Thrt;
pre->RTag = Thread;
(*Thrt)->rchild = pre;
return OK;
}
- 非递归遍历
//非递归遍历线索二叉树
Status InOrderTraverse(BiThrTree T) {
BiThrNode *p = T->lchild;
while(p!=T){
while(p->LTag==Link) p = p->lchild; //走向左子树的尽头
printf("%c",p->data );
while(p->RTag==Thread && p->rchild!=T) { //访问该结点的后续结点
p = p->rchild;
printf("%c",p->data );
}
p = p->rchild;
}
return OK;
}
在中序线索树找结点后继的规律是:若其右标志为1,则右链为线索,指示其后继,否则遍历其右子树时访问的第一个结点(右子树最左下的结点)为其后继;找结点前驱的规律是:若其左标志为1,则左链为线索,指示其前驱,否则遍历左子树时最后访问的一个结点(左子树中最右下的结点)为其前驱。
在后序线索树中找到结点的后继分三种情况:
1 若结点是二叉树的根,则其后继为空;
2 若结点是其双亲的右孩子,或是其双亲的左孩子且其双亲没有右子树,则其后继即为双亲结点;
*3 若结点是其双亲的左孩子,且其双亲有右子树,则其后继为双亲右子树上按后序遍历列出的第一个结点。
- 完整代码
如果粘贴复制代码就能学会,那你的就没有任何价值
#include <stdio.h>
#include <stdlib.h>
//函数状态结果代码
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
//Status是函数的类型,其值是函数结果状态代码
typedef int Status;
typedef char TElemType;
typedef enum { Link, Thread } PointerTag;
typedef struct BiThrNode {
TElemType data;
struct BiThrNode *lchild, *rchild;
PointerTag LTag;
PointerTag RTag;
}BiThrNode, *BiThrTree;
//线索二叉树初始化
Status CreateBiThrNode(BiThrTree * B) {
char ch;
scanf("%c", &ch);
if(ch=='#') *B = NULL;
else{
if(!((*B) = (BiThrNode *)malloc(sizeof(BiThrNode)))) exit(OVERFLOW);
(*B)->data = ch;
(*B)->LTag = Link;
(*B)->RTag = Link;
CreateBiThrNode(&(*B)->lchild);
CreateBiThrNode(&(*B)->rchild);
}
return OK;
}
//线索二叉树线索化
void InThreading(BiThrTree B,BiThrTree *pre) {
if(!B) return;
InThreading(B->lchild,pre);
if(!B->lchild){
B->LTag = Thread;
B->lchild = *pre;
}
if(!(*pre)->rchild){
(*pre)->RTag = Thread;
(*pre)->rchild = B;
}
*pre = B;
InThreading(B->rchild,pre);
}
//为线索二叉树添加头结点,使之可以双向操作
Status InOrderThreading(BiThrTree *Thrt,BiThrTree T){
if(!(*Thrt = (BiThrTree)malloc(sizeof(BiThrNode)))) exit(OVERFLOW);
(*Thrt)->LTag = Link;
(*Thrt)->RTag = Thread;
(*Thrt)->rchild = (*Thrt);
if(!T) {
(*Thrt)->lchild = (*Thrt);
return OK; //若根结点不存在,则该二叉树为空,让该头结点指向自身.
}
BiThrTree pre;
//令头结点的左指针指向根结点
pre = (*Thrt);
(*Thrt)->lchild = T;
//开始递归输入线索化
InThreading(T,&pre);
//此时结束了最后一个结点的线索化了,下面的代码把头结点的后继指向了最后一个结点.
//并把最后一个结点的后继也指向头结点,此时树成为了一个类似双向链表的循环.
pre->rchild = *Thrt;
pre->RTag = Thread;
(*Thrt)->rchild = pre;
return OK;
}
//非递归遍历线索二叉树
Status InOrderTraverse(BiThrTree T) {
BiThrNode *p = T->lchild;
while(p!=T){
while(p->LTag==Link) p = p->lchild; //走向左子树的尽头
printf("%c",p->data );
while(p->RTag==Thread && p->rchild!=T) { //访问该结点的后续结点
p = p->rchild;
printf("%c",p->data );
}
p = p->rchild;
}
return OK;
}
int main() {
BiThrTree B,T;
CreateBiThrNode(&B);
InOrderThreading(&T,B);
printf("中序遍历二叉树的结果为:");
InOrderTraverse(T);
printf("\n");
}
当然前序与后序遍历就可以写出来了!!!(自己动手改一遍!)
简单的运用
- (1)在中序线索二叉树中,查找结点*p的中序后继结点
BinThrNode *InorderSuccessor(BinThrNode *p)
{//在中序线索树中找结点*p的中序后继,设p非空
BinThrNode *q;
if (p->rtag==Thread) //*p的右子树为空
Return p->rchild; //返回右线索所指的中序后继
else{
q=p->rchild; //从*p的右孩子开始查找
while (q->ltag==Link)
q=q->lchild; //左子树非空时,沿左链往下查找
return q; //当q的左子树为空时,它就是最左下结点
} //end if
}
// 该算法的时间复杂度不超过树的高度h,即O(h)。
- 在中序线索二叉树中查找结点*p的中序前趋结点
BinThrNode *Inorderpre(BinThrNode *p)
{//在中序线索树中找结点*p的中序前趋,设p非空
BinThrNode *q;
if (p->ltag==Thread) //*p的左子树为空
return p->lchild; //返回左线索所指的中序前趋
else{
q=p->lchild; //从*p的左孩子开始查找
while (q->rtag==Link)
q=q->rchild; //右子树非空时,沿右链往下查找
return q; //当q的右子树为空时,它就是最右下结点
} //end if
}
AVL (平衡树)
平时有的比较多的地方有小根堆,或者拓扑排序中:
代码实现:
typedef struct AVLNode *Position;
typedef Position AVLTree; /* AVL树类型 */
struct AVLNode{
ElementType Data; /* 结点数据 */
AVLTree Left; /* 指向左子树 */
AVLTree Right; /* 指向右子树 */
int Height; /* 树高 */
};
int Max ( int a, int b )
{
return a > b ? a : b;
}
AVLTree SingleLeftRotation ( AVLTree A )
{ /* 注意:A必须有一个左子结点B */
/* 将A与B做左单旋,更新A与B的高度,返回新的根结点B */
AVLTree B = A->Left;
A->Left = B->Right;
B->Right = A;
A->Height = Max( GetHeight(A->Left), GetHeight(A->Right) ) + 1;
B->Height = Max( GetHeight(B->Left), A->Height ) + 1;
return B;
}
AVLTree DoubleLeftRightRotation ( AVLTree A )
{ /* 注意:A必须有一个左子结点B,且B必须有一个右子结点C */
/* 将A、B与C做两次单旋,返回新的根结点C */
/* 将B与C做右单旋,C被返回 */
A->Left = SingleRightRotation(A->Left);
/* 将A与C做左单旋,C被返回 */
return SingleLeftRotation(A);
}
/*************************************/
/* 对称的右单旋与右-左双旋请自己实现 */
/*************************************/
AVLTree Insert( AVLTree T, ElementType X )
{ /* 将X插入AVL树T中,并且返回调整后的AVL树 */
if ( !T ) { /* 若插入空树,则新建包含一个结点的树 */
T = (AVLTree)malloc(sizeof(struct AVLNode));
T->Data = X;
T->Height = 0;
T->Left = T->Right = NULL;
} /* if (插入空树) 结束 */
else if ( X < T->Data ) {
/* 插入T的左子树 */
T->Left = Insert( T->Left, X);
/* 如果需要左旋 */
if ( GetHeight(T->Left)-GetHeight(T->Right) == 2 )
if ( X < T->Left->Data )
T = SingleLeftRotation(T); /* 左单旋 */
else
T = DoubleLeftRightRotation(T); /* 左-右双旋 */
} /* else if (插入左子树) 结束 */
else if ( X > T->Data ) {
/* 插入T的右子树 */
T->Right = Insert( T->Right, X );
/* 如果需要右旋 */
if ( GetHeight(T->Left)-GetHeight(T->Right) == -2 )
if ( X > T->Right->Data )
T = SingleRightRotation(T); /* 右单旋 */
else
T = DoubleRightLeftRotation(T); /* 右-左双旋 */
} /* else if (插入右子树) 结束 */
/* else X == T->Data,无须插入 */
/* 别忘了更新树高 */
T->Height = Max( GetHeight(T->Left), GetHeight(T->Right) ) + 1;
return T;
}
基础知识点
术语
-
节点的度:一个节点含有的子树的个数称为该节点的度;
-
叶节点或终端节点:度为零的节点;
-
非终端节点或分支节点:度不为零的节点;
-
父亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;
-
兄弟节点:具有相同父节点的节点互称为兄弟节点;
-
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
-
树的高度或深度:树中节点的最大层次;
-
堂兄弟节点:父节点在同一层的节点互为堂兄弟;
-
节点的祖先:从根到该节点所经分支上的所有节点;
-
孙:以某节点为根的子树中任一节点都称为该节点的子孙。
-
森林:由m(m>=0)棵互不相交的树的集合称为森林;
-
满二叉树:一棵深度为k,且有2^k-1 (2的k次方减一)个节点称之为满二叉树
-
完全二叉树:完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。叶节点只能出现在最下层和次下层,并且最下面一层的结点都集中在该层最左边的若干位置的二叉树
二叉树的性质
1.在非空二叉树中,第i层的结点总数不超过2^(i-1),i>=1;
2.深度为h的二叉树最多有2^h-1个结点(h>=1),最少有h个结点;
3.对于任意一棵二叉树,如果其叶结点数为N0,而度数为2的结点总数为N2,则N0=N2+1;
4.具有n个结点的完全二叉树的深度为K =[log2n」+1(取下整数)
5.有N个结点的完全二叉树各结点如果用顺序方式存储,则结点之间有如下关系: 若I为结点编号则 如果I>1,则其父结点的编号为I/2;
6.完全二叉树,如果2I<=N,则其左儿子(即左子树的根结点)的编号为2I;若2I>N,则无左儿子; 如果2I+1<=N,则其右儿子的结点编号为2I+1;若2I+1>N,则无右儿子。
7.给定N个节点,能构成h(N)种不同的二叉树。h(N)为卡特兰数的第N项。h(n)=C(2*n,n)/(n+1)。
8.设有i个枝点,I为所有枝点的道路长度总和,J为叶的道路长度总和J=I+2i
二叉树的遍历三种方式,如下:
(1)前序遍历(DLR),首先访问根结点,然后遍历左子树,最后遍历右子树。简记根-左-右。
(2)中序遍历(LDR),首先遍历左子树,然后访问根结点,最后遍历右子树。简记左-根-右。
(3)后序遍历(LRD),首先遍历左子树,然后遍历右子树,最后访问根结点。简记左-右-根。
小结
对于二叉树,我们在算法中运用的比较多,不仅仅如此,我们一些计算机的底层有很多地方用到二叉树!!二叉树知识点可以分为三个部分:AVL,查找二叉,线索二叉树,这些树都有基本的功能实现!我们再将它们细分为各个小的知识点!有任何问题请发评论或者私信我,非常感谢你的阅读,加油!


tql
太强了
orz
棒!