下面来看一种特殊的线段树，即权值线段树
权值线段树经常用于处理区间第 $k$ 小的问题中
假设序列 $A = \{a_1, a_2, \cdots , a_n\} = \{-2, -6, 12, 3\}$
* 先将序列离散化成 $\{2， 1， 4， 3\}$，来看一下如何用线段树找第 $k$ 小

• $\textbf{for} \ \forall i \in [1, n]$，对每个 $i$ 都建立一棵表示区间 $[1, i]$ 的线段树
  在每个 $i$ 上查询区间 $[1, i]$ 的第 $k$ 小，复杂度是 $O(\log n)$
  从前往后扫描序列 $[1, n]$，对于第 $i$ 棵线段树，我们可以将第 $i-1$ 棵线段树复制过来，然后再修改

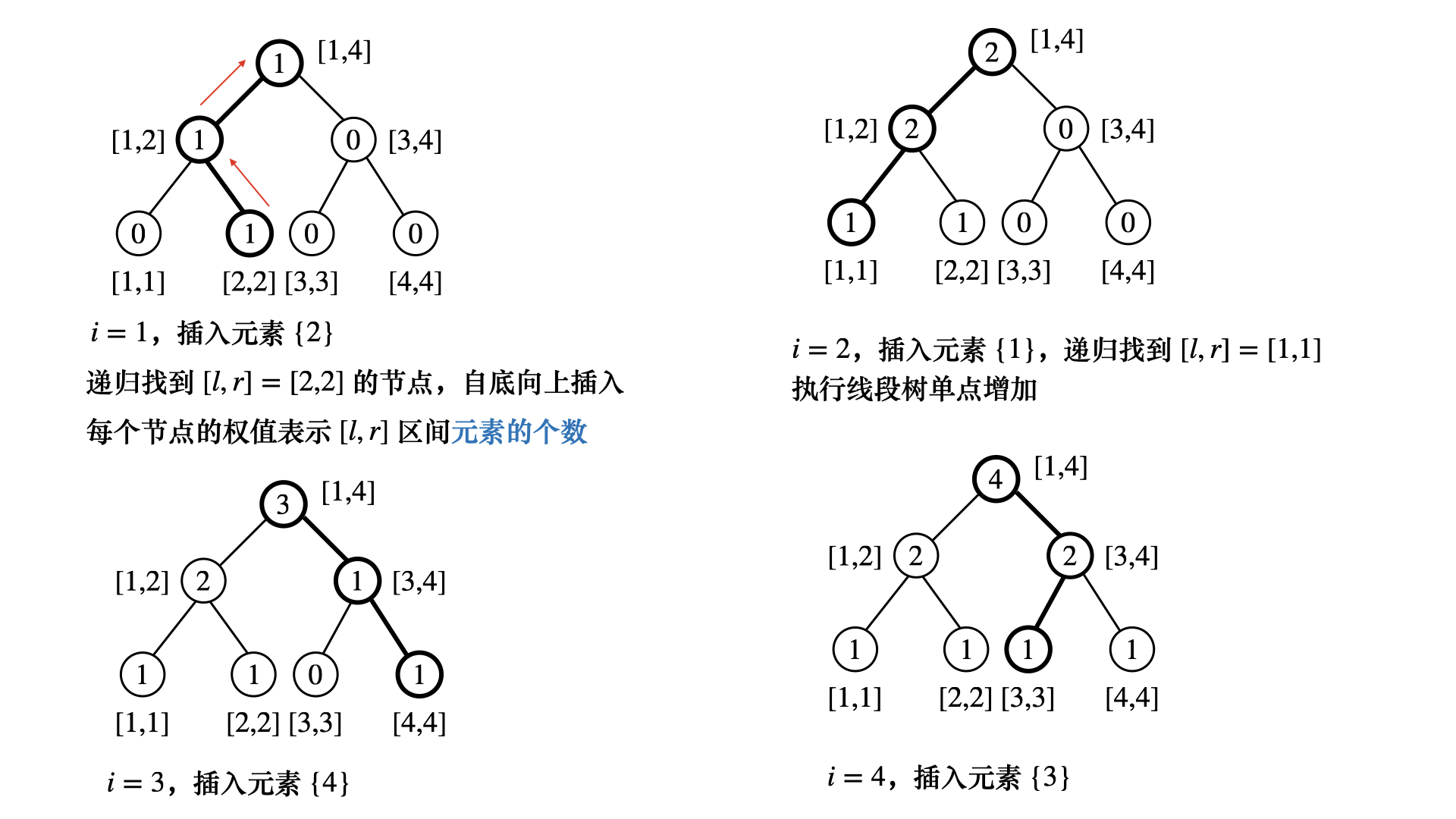
• 对于第 $i$ 棵线段树和第 $j$ 棵线段树 $(i < j)$，二者的拓扑结构完全一样，唯一的区别就是每个点的权值不同
  由于节点权值为： 节点表示的区间 $[l, r]$ 中有多少个元素？
  由前缀和思想，对于询问区间 $[L, R]$，$tree(R) - tree(L-1)$ 就表示 $[L, R]$ 中有多少个元素
  $tree(P) = tree(R)-tree(L-1)$ 仍然为一棵线段树，每个节点的拓扑结构不变，权值相减

• 这样就等于在 $tree(P)$ 上找第 $k$ 小，利用二分思想

• 如果 $tree(P).left$ 中元素个数 $\geqslant K$，递归在 $tree(P).left$ 中找第 $K$ 小

• 否则，令 $K’ = K-cnt(tree(P).left)$，在 $tree(P).right$ 中找第 $K’$ 小

对上述线段树进行可持久化
综上分析可以发现，算法的时间复杂度非常好，但是空间复杂度是 $O(n^2)$
观察这几棵线段树发现，实际上第 $i$ 棵线段树与第 $i-1$ 棵线段树比
只有加粗的部分不一样，剩下的都一样，加粗部分路径即发生修改的路径，
我们只要存储修改路径上的节点就可以了，如下图所示

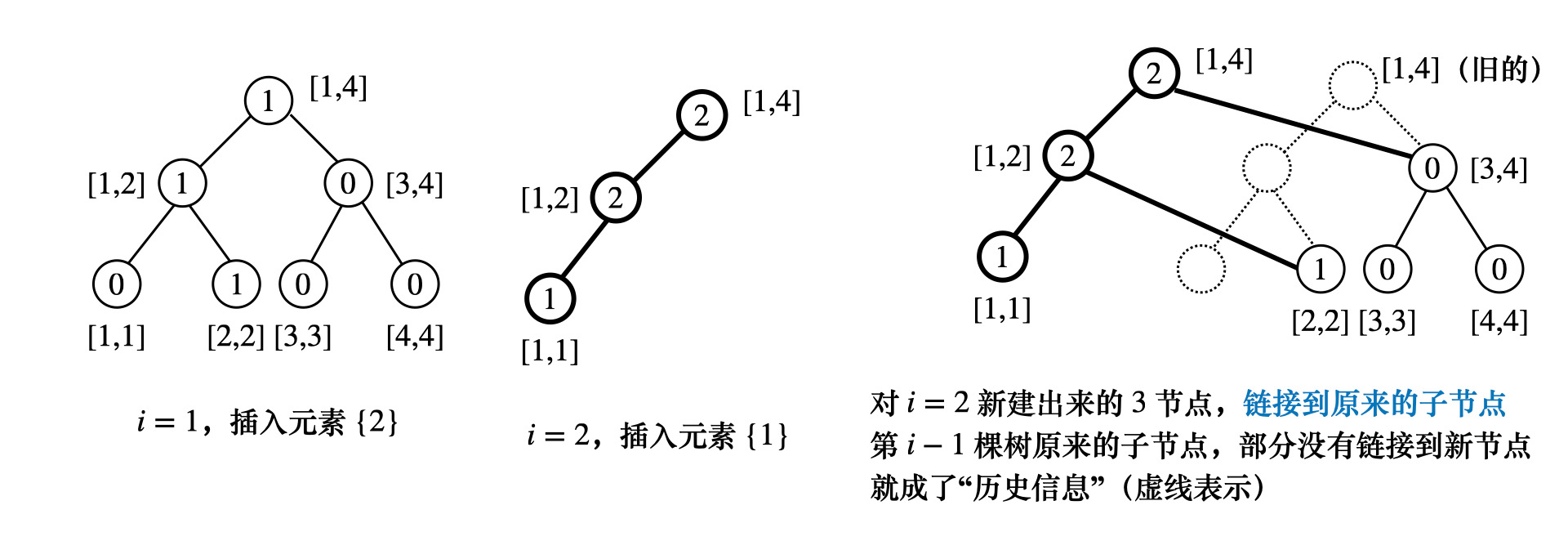
重要的细节
为了方便定位到每一棵线段树，需要建立一个 $root[\cdots]$ 数组
记录第 $i$ 棵线段树根节点的编号（或者说是数组地址）

K-th number
第 K 大数

细节，主席树执行单点修改的时候，是基于历史版本 $pre$
$\textbf{change}(pre, l, r, x), \ t[pre]$ 表示历史版本 $pre$ 的根节点
$t[pre]$ 表示的区间对应于 $[l, r]$，令 $mid \leftarrow (l+r)/2$

• $t[t_{pre}.l]$ 对应于区间 $[l, mid]$

• $t[t_{pre}.r]$ 对应于区间 $[mid+1, r]$

主席树执行单点修改

• 新建一个第 $i$ 阶段版本的新根节点 $t[i]$，基于旧版本 $pre$ 的根节点，对第 $i$ 阶段的新根节点进行修改
  $t[pre] \xrightarrow{\text{update}: \ f(P)} t[i]$，执行 $f(P)$ 操作

• 自顶向下递归历史版本的线段树，递归对 $t_{pre}$ 的子树进行修改

• 如果 $x \leqslant mid$，那么基于历史版本 $t[t_{pre}.l]$，对区间 $[l, mid]$ 执行 $f(P)$ 操作，并且建立新节点 $u$
  递归返回新节点编号 $u$，并且令 $t[i].l = u$

• 如果 $x > mid$，基于历史版本 $t[t_{pre}.r]$ 修改区间 $[mid+1, r]$ 并且建立新节点 $u$
  递归返回，令 $t[i].r = u$

主席树查询区间 $[u, v]$ 第 $k$ 小，利用前缀和思想，令 $u \leftarrow u-1, v \leftarrow v$
考虑 $t[u]$ 和 $t[v]$ 这两棵线段树

• 注意到版本 $u$ 表示的线段树 $t[u]$ 和版本 $v$ 表示的线段树 $t[v]$ ，对区间的划分是相同的
  都表示区间 $[1\cdots n]$，因为我们是从前往后遍历，在区间中执行单点增加

• $t[u]$ 这棵线段树，表示区间是 $[1\cdots u] \cup [u+1 \cdots n]$
  实际上我们只统计了 $[1\cdots u]$ 的信息，对于 $[u \cdots n]$ 中的点，其权值为 $0$
  所以 $t[u]$ 这棵线段树，等价于存储了 $[1\cdots u]$ 区间内一共有多少个点
  其表示的区间为 $[l, r] = [1, n]$（对于 $[u+1, n]$ 中的点，其权值为 $0$，因为在版本 $u$ 并未添加 $u$ 之后的点）

• 同理，$t[v]$ 这棵线段树存储了 $[1\cdots v]$ 区间内一共有多少个点
  $x = t[v] - t[u]$ 表示区间 $[u+1, v]$ 中一共有 $x$ 个点
  （实际上根节点表示的区间一般仍然为 $[1, n]$，只不过 $v$ 之后的点并没有添加，所以 $[v+1, n]$ 的权值为 $0$）

• $x = t_v.sum - t_u.sum$ 表示区间 $[u+1, v]$ 中有 $x$ 个数，那么第 $k$ 小可以用二分思想解决
  由于这两个版本的线段树对于区间的划分完全一致，所以同时递归这两棵线段树
  这两棵线段树根节点表示区间为 $[l, r]=[1,n], \ mid = (l+r)/2$
  根节点的地址为 $u = root(u-1), v = root(v)\quad query(u, v, l, r, K):$
  (是 $u-1$ 不是 $u$，因为我们询问区间 $[u, v]$)

• $t[t_u.l], \ t[t_v.l]$ 表示区间 $[l, mid]$, 其中的元素个数为 $cnt = t[t_v.l].sum - t[t_u.l].sum$
  如果 $K \leqslant cnt$，同时递归左子树，$query(t_u.l, \ t_v.l, \ l, mid, K)$

• $t[t_u.r], t[t_v.r]$ 表示区间 $[mid+1, r]$，如果 $K > cnt$，那么同时递归右子树
  在右子树中找到第 $K - cnt$ 小的元素，$query(t_u.r,\ t_v.r, \ mid+1, r, K-cnt)$

class wsegTree {
public:
    struct node {
        int l, r;
        int sum;
    };

    int n;
    int tot;
    vector<node> t;

    wsegTree() = default;
    wsegTree(int _n) : n(_n) {
        assert(n > 0);
        tot = 0;
        t.resize(n << 5);
    }
    void clear() {
        tot = 0;
        fill(t.begin(), t.end(), node());
    }

    int build(int l, int r) {
        int u = ++tot;
        if (l >= r) return u;
        int mid = (l + r) >> 1;
        t[u].l = build(l, mid);
        t[u].r = build(mid+1, r);
        return u;
    }

    int change(int pre, int l, int r, int x) {
        int u = ++tot;
        t[u] = t[pre];
        t[u].sum = t[pre].sum + 1;
        if (l >= r) return u;

        int mid = (l + r) >> 1;
        if (x <= mid) t[u].l = change(t[pre].l, l, mid, x);
        else t[u].r = change(t[pre].r, mid + 1, r, x);

        return u;
    }

    int query(int u, int v, int l, int r, int K) {
        if (l == r) return l;
        int cnt = t[t[v].l].sum - t[t[u].l].sum;
        int mid = (l + r) >> 1;

        if (K <= cnt) return query(t[u].l, t[v].l, l, mid, K);
        else return query(t[u].r, t[v].r, mid+1, r, K-cnt);
    }
};

const int maxn = 100000 + 10;
wsegTree wseg(maxn);
int n, m, root[maxn], a[maxn], b[maxn];

int main() {
    freopen("input.txt", "r", stdin);
    scanf("%d%d", &n, &m);

    map<int, int> M;
    int idx = 0;
    for (int i = 1; i <= n; i++) scanf("%d", &a[i]), M[a[i]] = 0;
    for (auto &x : M) {
        x.second = ++idx, b[idx] = x.first;
    }

    for (int i = 1; i <= n; i++) {
        root[i] = wseg.change(root[i-1], 1, idx, M[a[i]]);
    }

    while (m--) {
        int u, v, k;
        scanf("%d%d%d", &u, &v, &k);
        int res = wseg.query(root[u-1], root[v], 1, idx, k);
        printf("%d\n", b[res]);
    }
}

主席树代码建议当模版背下来
调用时候直接

wsegTree wseg(maxn);

int main() {
    root[i] = wseg.change(root[i-1], ....)
}