问题描述

在一个神秘的森林里，住着一个小精灵名叫小蓝。有一天,他偶然发现了一个隐藏在树洞里的宝藏，里面装满了闪烁着美丽光芒的宝石。这些宝石都有着不同的颜色和形状，但最引人注目的是它们各自独特的“闪亮度”属性。每颗宝石都有一个与生俱来的特殊能力，可以发出不同强度的闪光。小蓝共找到了N枚宝石，第i枚宝石的“闪亮度”属性值为H,小蓝将会从这N枚宝石中选出三枚进行组合，组合之后的精美程度S可以用以下公式来衡量:

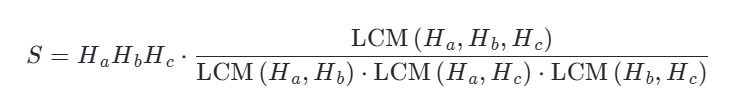
其中LCM示的是最小公倍数函数。
小蓝想要使得三枚宝石组合后的精美程度S可能的高，请你帮他找出精美程
度最高的方案。如果存在多个方案S值相同,优先选择按照H值升序排列后
字典序最小的方案。

输入格式

第一行包含一个整数N表示宝石个数。
第二行包含N个整数表示N个宝石的“闪亮度”。

输出格式

输出一行包含三个整数表示满足条件的三枚宝石的“闪亮度”。

样例输入

5
1 2 3 4 9

样例输出

1 2 3

评测用例规模与约定

对于30%的评测用例:3≤N≤100,1≤Hi≤1000。
对于60%的评测用例:3≤N≤2000。
对于100%的评测用例:3≤N≤10⁵,1≤Hi≤10⁵。

无脑暴力 30%

先进行排序，再找到值最大的符合条件的三个数
注意开long long，不然会爆

C++ 代码

#include <bits/stdc++.h>
using namespace std;
#define int long long
int gcd(int a, int b)
{
    if (b == 0)
        return a;
    return gcd(b, a % b);
}
int lcm(int a, int b)
{
    return a * b / gcd(a, b);
}
int gcd3(int a, int b, int c)
{
    return gcd(gcd(a, b), c);
}
int lcm3(int a, int b, int c)
{
    return lcm(lcm(a, b), c);
}
signed main()
{
    int n;
    cin >> n;
    vector<int> a(n), b(3);
    for (int i = 0; i < n; i++)
        cin >> a[i];
    sort(a.begin(), a.end());
    int ans = 0;
    for (int i = 0; i < n; i++)
    {
        for (int j = i + 1; j < n; j++)
        {
            for (int k = j + 1; k < n; k++)
            {
                int s = a[i] * a[j] * a[k] * lcm3(a[i], a[j], a[k]) / (lcm(a[i], a[j]) * lcm(a[i], a[k]) * lcm(a[j], a[k]));
                if (s > ans)
                {
                    ans = s;
                    b[0] = a[i];
                    b[1] = a[j];
                    b[2] = a[k];
                }
            }
        }
    }
    cout << b[0] << " " << b[1] << " " << b[2];
    return 0;
}

优化暴力 30%

可以将整个公式化简为gcd(a,b,c)
但30%测试数据直接从10个变成2000个了，所以还是过不了
但为后续写法作了铺垫

C++ 代码

#include <bits/stdc++.h>
using namespace std;
#define int long long
int gcd(int a, int b)
{
    if (b == 0)
        return a;
    return gcd(b, a % b);
}
int gcd3(int a, int b, int c)
{
    return gcd(gcd(a, b), c);
}
signed main()
{
    int n;
    cin >> n;
    vector<int> a(n), b(3);
    for (int i = 0; i < n; i++)
        cin >> a[i];
    sort(a.begin(), a.end());
    int ans = 0;
    for (int i = 0; i < n; i++)
    {
        for (int j = i + 1; j < n; j++)
        {
            for (int k = j + 1; k < n; k++)
            {
                int s = gcd3(a[i], a[j], a[k]);
                if (s > ans)
                {
                    ans = s;
                    b[0] = a[i];
                    b[1] = a[j];
                    b[2] = a[k];
                }
            }
        }
    }
    cout << b[0] << " " << b[1] << " " << b[2];
    return 0;
}

逆向思维 100%

由于数据量达到10⁵，所以暴力遍历不可取
寻找abc满足S最大，
反过来想，就是寻找S，存在abc
S=gcd(a,b,c)，说明abc都是S的倍数
假定S为某个值，凑出3个倍数a,b,c

C++ 代码

#include <bits/stdc++.h>
using namespace std;
const int h = 1e5;
int main()
{
    // m记录宝石个数
    int n, m[h + 1] = {}, t, max = 0;
    cin >> n;
    for (int i = 0; i < n; i++)
    {
        // 亮度为t的宝石个数
        cin >> t;
        m[t]++;
        // 精美程度一定小于等于最大的亮度
        if (t > max)
            max = t;
    }
    // 假设精美程度为i，从大到小遍历i的所有可能值
    for (int i = max; i >= 1; i--)
    {
        int ans = 0, cnt = 0, num[3] = {};
        for (int j = i; j <= max; j += i)
        {
            // 若m[j]有值，则找到m[j]个j的宝石
            ans += m[j];
            // 统计找到的宝石，直到三枚
            for (int k = 0; k < m[j] && cnt < 3; k++)
                num[cnt++] = j;
            // 找到了三枚宝石，输出
            if (ans >= 3)
            {
                cout << num[0] << " " << num[1] << " " << num[2];
                return 0;
            }
        }
    }
    return 0;
}