线段树
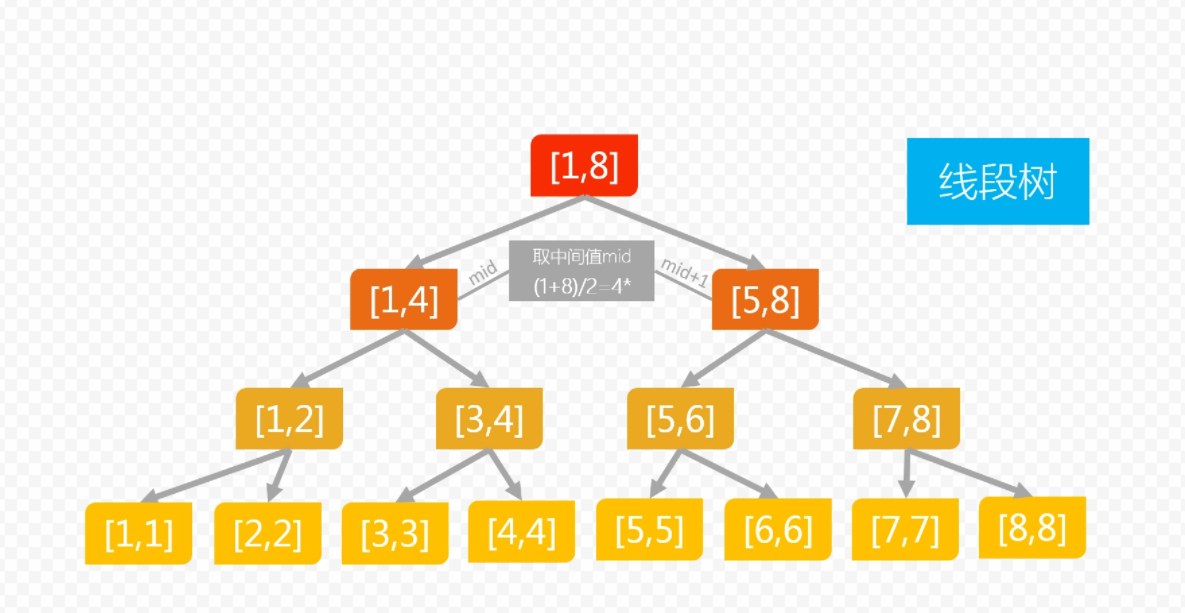
线段树是一种二叉搜索树,与区间树相似,它将一个区间划分成一些单元区间,每个单元区间对应线段树中的一个叶结点。
使用线段树可以快速的查找某一个节点在若干条线段中出现的次数,时间复杂度为$O(logN)$。而未优化的空间复杂度为2N,实际应用时一般还要开$4N$的数组以免越界,因此有时需要离散化让空间压缩。
用结构体数组定义线段树
const int N = 100007;
int A[N];//原始数组
//用结构体数组定义线段树
struct SegTreeNode{
int val;//保存节点值
int lazy;
//懒惰标记,更新节点时可用来节约效率
}SegTree[N<<2];
线段树的构造
//线段树的构造
void PushUp(int rt){//用来求父节点的总和
SegTree[rt].val = SegTree[rt<<1].val+SegTree[rt<<1|1].val;
}
void PushUp(int rt){//求解点最大值
SegTree[rt].val = max(SegTree[rt<<1].val,SegTree[rt<<1|1].val);
}
void build(int l,int r,int rt){// 1 13 1
SegTree[rt].lazy = 0;
if(l == r){
SegTree[rt].val = A[l];
return;//找到最底层后返回更新父节点的和PushUp
}
int m = (l+r) / 2;
build(l,m,rt<*2);
build(m+1,r,rt*2+1);
PushUp(rt);
}
单点更新 A[L] += C
void Update(int L,int C,int l,int r,int rt){
if(l == r){
SegTree[rt].val +=C;//改变每个节点具体的值
return;
}
int m = (l+r)>>1;
if(L <= m) Update(L,C,l,m,rt<<1);
else Update(L,C,m+1,r,rt<<1|1);
PushUp(rt);//回溯 向上更新
}
区间查询
int Query(int L,int R,int l,int r,int rt){
if(L<= l && r<=R)//当前区间包含操作区间
return SegTree[rt].val;
if(L>r || R<l) return 0;
int m = (l+r)>>1;
// int ans=0;
// if(L<=m) ans+=Query(L,R,l,m,rt<<1);
// if(r>m) ans+=Query(L,R,m+1,r,rt<<1|1);
// return ans;
return Query(L,R,l,m,rt<<1)+Query(L,R,m+1,r,rt<<1|1);
}
区间更新(对区间的节点进行操作)
void Update(int L,int R,int C,int l,int r,int rt){
if(L<=l && r<=R){
SegTree[rt].val += C*(r-l+1)//更新父节点数字和
SegTree[rt].lazy+=C;
return;
}
int m = (l+r)>>1;
PushDown(rt,m-l+1,r-m);
if(L<=m) Update(L,R,C,l,m,rt<<1);
if(R > m) Update(L,R,C,m+1,r,rt<<1|1);
PushUp(rt);
}
void PushDown(int rt,int ln,int rn){
if(SegTree[rt].lazy){
SegTree[rt<<1].lazy+=SegTree[rt].lazy;
SegTree[rt<<1|1].lazy+=SegTree[rt].lazy;
SegTree[rt<<1].val+=SegTree[rt].lazy*ln;
SegTree[rt<<1|1].val+=SegTree[rt].lazy*rn;
SegTree[rt].lazy = 0//清空原节点标记
}
}
区间更新的区间查询(询问A[L..R]的和)
int Query(int L,int R,int l,int r,int rt){
if(L<=l && r<=R)
return SegTree[rt].val;
if(L > r || R<l) return 0;
int m =(l+r)>>1;
PushDown(rt,m-l+1,r-m);
return Query(L,R,l,m,rt<<1) + Query(L,R,m+1,r,rt<<1|1);
}
例题补充:
HDU 1002 I Hate It
【问题描述】
很多学校流行一种比较的习惯。老师们很喜欢询问,从某某到某某当中,分数最高的是多少。
这让很多学生很反感。
不管你喜不喜欢,现在需要你做的是,就是按照老师的要求,写一个程序,模拟老师的询问。当然,老师有时候需要更新某位同学的成绩。
【输入形式】
本题目包含多组测试,请处理到文件结束。
在每个测试的第一行,有两个正整数 N 和 M ( 0<N<=200000,0<M<5000 ),分别代表学生的数目和操作的数目。
学生ID编号分别从1编到N。
第二行包含N个整数,代表这N个学生的初始成绩,其中第i个数代表ID为i的学生的成绩。
接下来有M行。每一行有一个字符 C (只取'Q'或'U') ,和两个正整数A,B。
当C为'Q'的时候,表示这是一条询问操作,它询问ID从A到B(包括A,B)的学生当中,成绩最高的是多少。
当C为'U'的时候,表示这是一条更新操作,要求把ID为A的学生的成绩更改为B。
【输出形式】
对于每一次询问操作,在一行里面输出最高成绩。
in
5 6
1 2 3 4 5
Q 1 5
U 3 6
Q 3 4
Q 4 5
U 2 9
Q 1 5
out
5
6
5
9
#include <bits/stdc++.h>
using namespace std;
int t,n,m;
typedef long long ll;
const int N = 100005;
int a[N];
struct node{
int val,lazy;
}e[N<<2];
void pushup(int rt){//求的是最大值
e[rt].val = max(e[rt<<1].val,e[rt<<1|1].val);
}
void build(int l,int r,int rt){
if(l==r) {
e[rt].val = a[l];
return;
}
int m = (l+r)>>1;
build(l,m,rt<<1);
build(m+1,r,rt<<1|1);
pushup(rt);
}
void update(int a,int c,int l,int r,int rt){
if(l == r){
e[rt].val = c;
return;
}
int m =(l+r)>>1;
if(a <= m) update(a,c,l,m,rt<<1);
update(a,c,m+1,r,rt<<1|1);
pushup(rt);
}
ll query(int a,int b,int l,int r,int rt){
if(a>r || b<l) return 0;
if(a<=l && b>=r) return e[rt].val;
// pushdown(rt,l,r);
int mid=(l+r)>>1;
return max(query(a,b,l,mid,rt<<1),query(a,b,mid+1,r,rt<<1|1));
}
int main()
{
char op;
int x,y;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) cin >> a[i];
build(1,n,1);
while(m--){
getchar();
cin >> op;
cin >> x >>y;
if(op=='U')
update(x,y,1,n,1);
else
printf("%lld\n",query(x,y,1,n,1));
}
return 0;
}
HDU-1001 张煊的金箍棒(2)
【问题描述】
张煊的金箍棒升级了!
升级后的金箍棒是由几根相同长度的金属棒连接而成(最开始都是铜棒,从1到N编号);
张煊作为金箍棒的主人,可以对金箍棒施以任意的变换,每次变换操作就是将一段连续的金属棒(从X到Y编号)改为铜棒,银棒或金棒。
金箍棒的总价值计算为N个金属棒的价值总和。其中,每个铜棒价值为1;每个银棒价值为2;每个金棒价值为3。
现在,张煊想知道多次执行操作后的金箍棒总价值。
【输入形式】
输入的第一行是测试数据的组数(不超过10个)。
对于每组测试数据,第一行包含一个整数N(1 <= N <= 100000),表示金箍棒有N节金属组成,第二行包含一个整数Q(0 <= Q <= 100,000),表示执行变换的操作次数。
接下来的Q行,每行包含三个整数X,Y,Z(1 <= X <= Y <= N,1 <= Z <= 3),它定义了一个操作:将从X到Y编号的金属棒变换为金属种类Z,其中Z = 1代表铜棒,Z = 2代表银棒,Z = 3代表金棒。
【输出形式】
对于每组测试数据,请输出一个数字,表示操作后金箍棒的总价值。
in
1
10
2
1 5 2
5 9 3
out
24
#include <bits/stdc++.h>
using namespace std;
const int N = 100005;
typedef long long ll;
ll t,n,m;
struct node{
int val,lazy;
}e[N<<2];
void pushup(int rt){
e[rt].val = e[rt<<1].val+e[rt<<1|1].val;
}
void build(int l,int r,int rt){
if(l==r) {
e[rt].val = 1;
return;
}
int m = (l+r)>>1;
build(l,m,rt<<1);
build(m+1,r,rt<<1|1);
pushup(rt);
}
void pushdown(int rt,int l,int r){
if(e[rt].lazy){
e[rt<<1].lazy=e[rt].lazy;
e[rt<<1|1].lazy=e[rt].lazy;
int mid =(l+r)>>1;
e[rt<<1].val=e[rt].lazy*(mid-l+1);
e[rt<<1|1].val=e[rt].lazy*(r-mid);
e[rt].lazy=0;
}
}
void update(int L,int R,int c,int l,int r,int rt){
if(L>r || R<l) return;
if(L<=l && r<=R){
e[rt].val = c*(r-l+1);
e[rt].lazy = c;
return;
}
pushdown(rt,l,r);
int m =(l+r)>>1;
if(L<=m) update(L,R,c,l,m,rt<<1);
if(R>m) update(L,R,c,m+1,r,rt<<1|1);
pushup(rt);
}
int query(int a,int b,int l,int r,int rt){
if(a>r || b<l) return 0;
if(a<=l && b>=r) return e[rt].val;
pushdown(rt,l,r);//只要会用到下面的节点就需要更新
int mid=(l+r)>>1;
return query(a,b,l,mid,rt<<1)+query(a,b,mid+1,r,rt<<1|1);
}
int main() {
scanf("%lld",&t);
while(t--){
scanf("%lld",&n);
build(1,n,1);
scanf("%lld",&m);
while (m--){
ll x, y,z;
scanf("%lld%lld%lld",&x,&y,&z);
update(x,y,z,1,n,1);
}
printf("%lld\n",query(1,n,1,n,1));
}
return 0;
}


写的真好,一语胜csdn千言
哈哈哈哈哈!