主要讲用Dijkstra算法和SPFA算法求最短路（一些有负环的题就不能用Dij了）。
最短路就是求两点之间的最短路径。
最短路径怎么求呢？
1.更新。
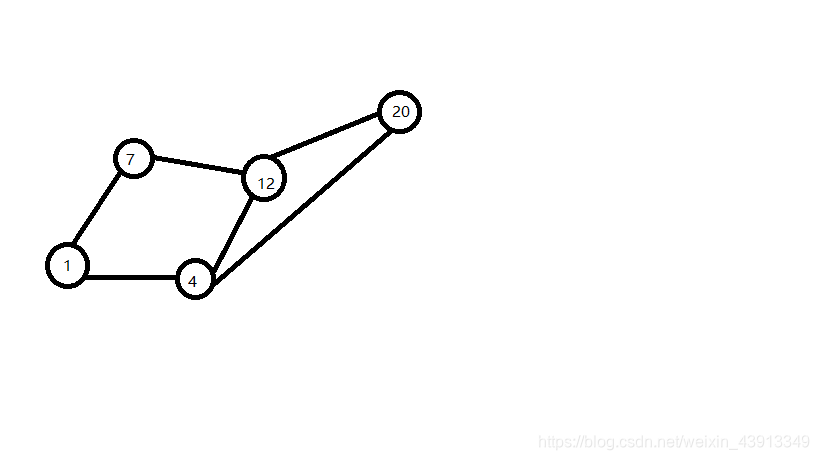先赋予厚望（假设无穷大）
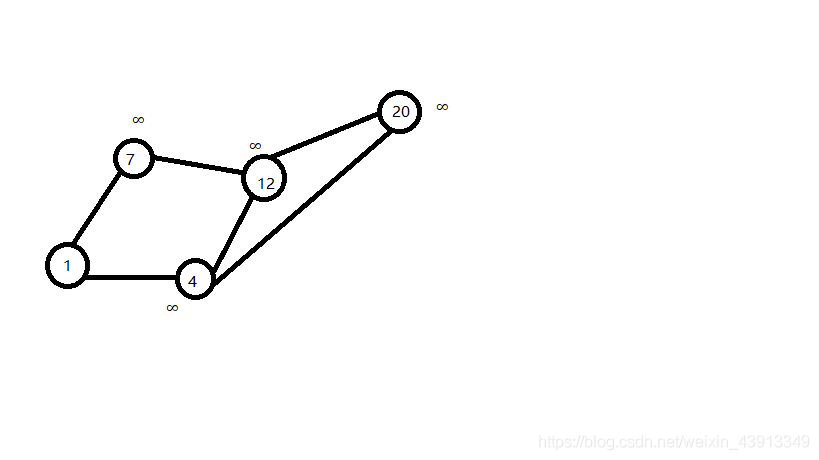然后依次更新
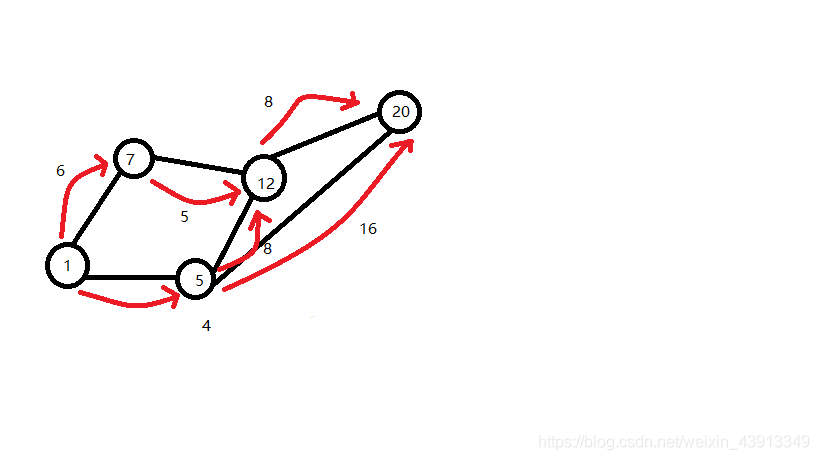
通过起点1来比较哪条路到终点20最短
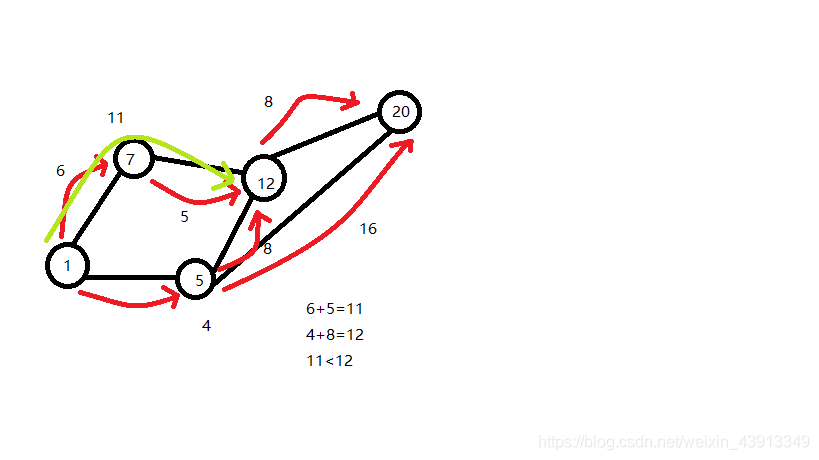暂时选择这条绿色的路
继续比较
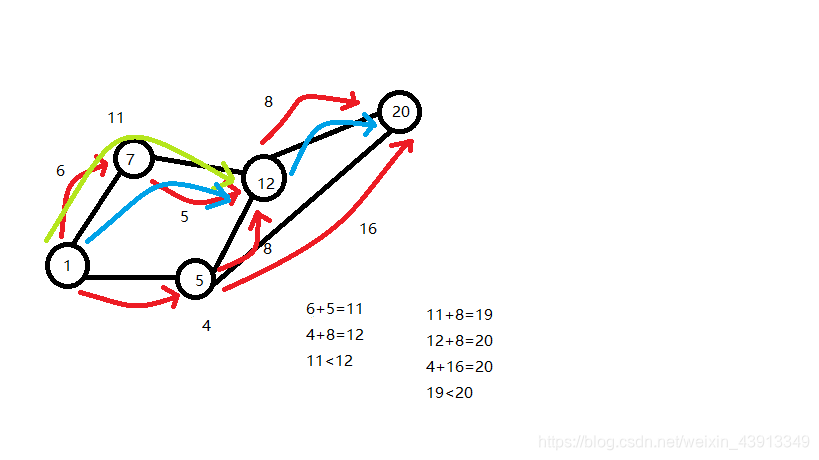
所以蓝色的路是最短的。
然后看一道纯模板题。
骑车比赛
Description
小信准备去参加骑车比赛，比赛在 n 个城市间进行，编号从 1 到 n。选手们都从城市 1 出发，终点在城市 n。
已知城市间有 m 条道路，每条道路连接两个城市，注意道路是双向的。现在小信知道了他经过每条道路需要花费的时间，他想请你帮他计算一下，他这次比赛最少需要花多少时间完成。
Input
第一行输入两个整数 n,m（1≤n≤1,000,1≤m≤5,000），分别代表城市个数和道路总数。接下来输入 m 行，每行输入三个数字 a,b,c（1≤a,b≤n,1≤c≤200），分别代表道路的起点和道路的终点，以及小信骑车通过这条道路需要花费的时间。保证输入的图是连通的。
Output
输出一行，输出一个整数，输出小信完成比赛需要的最少时间。
Sample Input 1
5 6
1 2 2
2 3 3
2 5 5
3 4 2
3 5 1
4 5 1
Sample Output 1
6
典型的最短路
Dijkstra模板：
#include<bits/stdc++.h>
using namespace std;
int n,m;
struct node{//结构体
int v,w;
node(){ };
node(int _v,int _w){
v=_v;
w=_w;
}
};
vector <node> g[10100];
bool vis[10100];
int dst[10100];
void add(int u,int v,int w){//建图
g[u].push_back(node(v,w));
g[v].push_back(node(u,w));
}
void dij(int s){
memset(dst,0x3f,sizeof dst);
int u = s;
dst[u]=0;
vis[u]=1;
int nn=n;
while(nn--){
for(int j=0;j<g[u].size();j++){
int v = g[u][j].v;
int w = g[u][j].w;
dst[v] = min(dst[v],dst[u]+w);
}
int mi=0x3f3f3f3f;//无穷大
for(int j=1;j<=n;j++){
if(!vis[j]&&mi>dst[j]){
mi = dst[j];
u = j;
}
}
vis[u] = 1;
}
}
int main(){
cin >> n >>m;
int u,v,w;
while (m--){
cin >> u >> v >> w;
add(u,v,w);
}
dij(1);
cout << dst[n];
return 0;
}
SPFA模板
#include<bits/stdc++.h>
using namespace std;
const int maxn=1010;
const int inf=0x3f3f3f3f;
int n,m;
struct node{
int v,w;
node(){ }
node(int _v,int _w){
v=_v;
w=_w;
}
};
vector <node> g[maxn];
int dst[maxn];
queue <int> qu;
int inq[maxn];
int add(int u,int v,int w){
g[u].push_back(node(v,w));
g[v].push_back(node(u,w));
}
void spfa(int s){
memset(dst,inf,sizeof dst);
int u=s;
dst[u]=0;
qu.push(u);
inq[u]=1;
while(!qu.empty()){
u=qu.front();
qu.pop();
inq[u]=0;
for(int i=0;i<g[u].size();i++){
int v=g[u][i].v;
int w=g[u][i].w;
if(dst[v]>dst[u]+w){
dst[v]=dst[u]+w;
if(!inq[v]){
qu.push(v);
inq[v]=1;
}
}
}
}
}
int main(){
cin >> n >> m;
int u , v , w;
while (m--){
cin >> u >> v >> w;
add(u,v,w);
}
spfa(1);
cout << dst[n]<<endl;
return 0;
}
迷阵突围
Description
小信陷入了坐标系上的一个迷阵，迷阵上有 n个点，编号从 1 到 n。小信在编号为 1 的位置，他想到编号为 n 的位置上。小信当然想尽快到达目的地，但是他觉得最短的路径可能有风险，所以他会选择第二短的路径。现在小信知道了 n 个点的坐标，以及哪些点之间是相连的，他想知道第二短的路径长度是多少。
注意，每条路径上不能重复经过同一个点。
Input
第一行输入两个整数 n (1≤n≤200) 和 m，表示一共有 n 个点和 m 条边。
接下来输入 n 行，每行输入两个整数 xi,yi (−500≤xi,yi≤500)，代表第 i 个点的坐标。
接下来输入 m 行，每行输入两个整数 pj,qj (1≤pj,qj≤n)，表示点 pj 和点 qj 之间相连。
Output
输出一行，输出包含一个数，表示第二短的路径长度（小数点后面保留两位），如果第一短路径有多条，则答案就是第一最短路径的长度；如果第二最短路径不存在，则输出 -1。
Sample Input 1
3 3
1 1
2 2
3 2
1 2
2 3
1 3
Sample Output 1
2.41
模板改进。（两个dij函数）
#include<bits/stdc++.h>
using namespace std;
int n,m;
struct node{
int v;
double w;
node(){ };
node(int _v,double _w){
v=_v;
w=_w;
}
};
vector <node> g[10100];
bool vis[10100];
double dst[10100];
int x[10100],y[10100];
int pre[10100];
void add(int u,int v,double w){
g[u].push_back(node(v,w));
g[v].push_back(node(u,w));
}
void dij(int s){
memset(vis,0,sizeof vis);
for(int i=1;i<=n;i++){
dst[i]=1e20;
}
int u = s;
dst[u]=0;
vis[u]=1;
int nn=n;
while(nn--){
for(int j=0;j<g[u].size();j++){
int v = g[u][j].v;
double w = g[u][j].w;
if(dst[v]>dst[u]+w){
dst[v]=dst[u]+w;
pre[v]=u;
}
}
double mi=1e20;
for(int j=1;j<=n;j++){
if(!vis[j]&&mi>dst[j]){
mi = dst[j];
u = j;
}
}
vis[u] = 1;
}
}
void dij2(int s,int uu,int vv){
memset(vis,0,sizeof vis);
for(int i=1;i<=n;i++){
dst[i]=1e20;
}
int u = s;
dst[u]=0;
vis[u]=1;
int nn=n;
while(nn--){
for(int j=0;j<g[u].size();j++){
int v = g[u][j].v;
double w = g[u][j].w;
if(uu ==u && vv==v || uu==v && vv == u){
continue;
}
dst[v] = min(dst[v],dst[u]+w);
}
double mi=1e20;
for(int j=1;j<=n;j++){
if(!vis[j]&&mi>dst[j]){
mi = dst[j];
u = j;
}
}
vis[u] = 1;
}
}
int main(){
cin >> n >>m;
int u,v;
double w;
for(int i=1;i<=n;i++){
cin >> x[i] >>y[i];
}
while (m--){
cin >> u >> v;
w=sqrt((x[u]-x[v])*(x[u]-x[v])+(y[u]-y[v])*(y[u]-y[v]));
add(u,v,w);
}
dij(1);
double mi=1e20;
for(int i=n;pre[i]!=0;i=pre[i]){
dij2(1,i,pre[i]);
mi=min(mi,dst[n]);
}
if(mi == 1e20){
cout << "-1"<<endl;
}else{
cout<<fixed<<setprecision(2)<<mi<<endl;
}
return 0;
}
