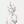朴素版完全背包（三个循环）

错误代码：

#include<bits/stdc++.h>

using namespace std;

const int N=1010;

int n,m,v[N],w[N],dp[N][N];

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>v[i]>>w[i];

    for(int i=1;i<=n;i++)
      for(int j=1;j<=m;j++)
        for(int k=0;k*v[i]<=j;k++)
        {
            dp[i][j]=max(dp[i-1][j],dp[i-1][j-k*v[i]]+k*w[i]);
        }

    cout<<dp[n][m];

    return 0;
}

回顾思维过程：

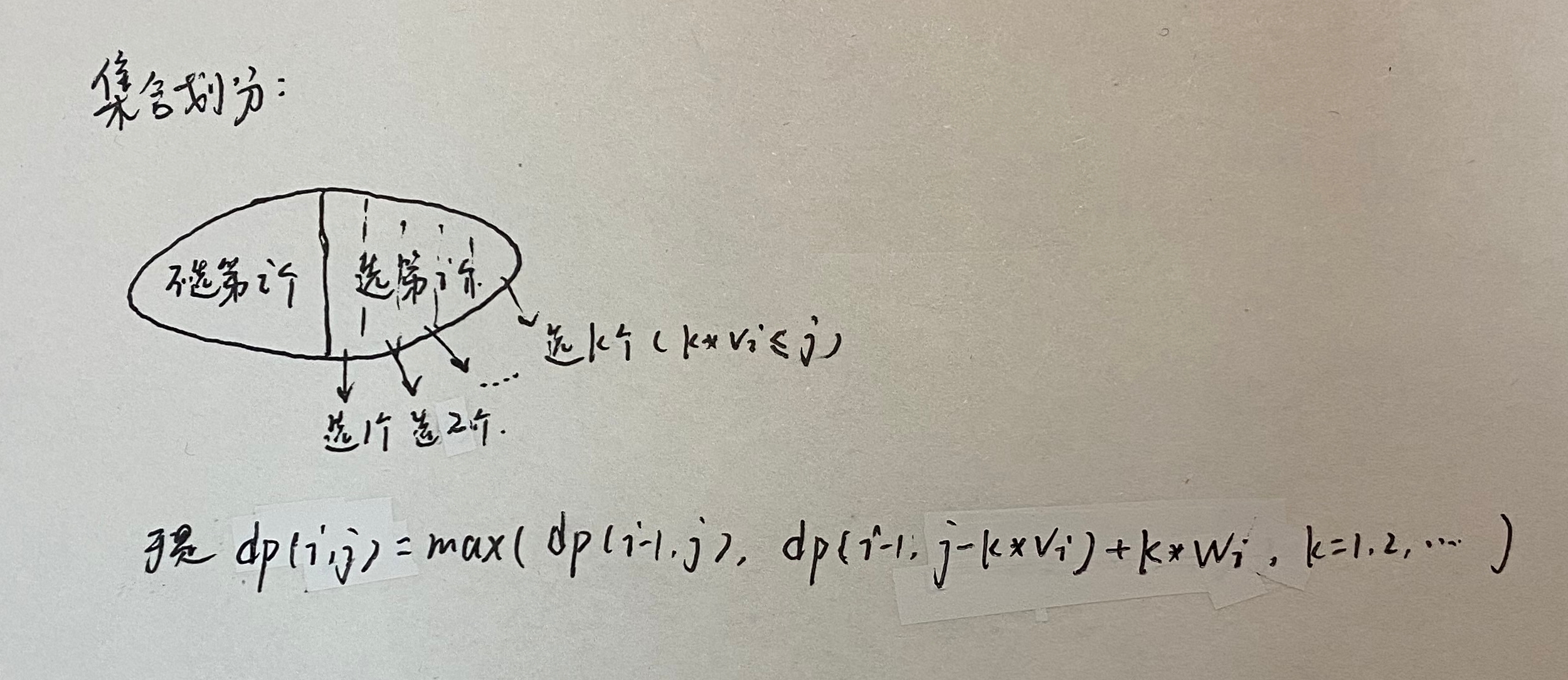
这个集合划分方式是没有问题的，是实现出了问题
我们这个三重循环，前两重遍历每个状态，通过状态转移方程dp[i][j]=max(dp[i-1][j],dp[i-1][j-kv[i]]+kw[i],k=1,2,…)求出该位置状态值，但第三层循环出了问题，没有达到状态转移的效果，这个错误的代码，每次比较dp[i-1][j]和dp[i-1][j-kv[i]]+kw[i],每次的较大值赋给dp[i][j],循环直到背包塞不下,假设循环了x次，前x-1次的比较赋值都是无意义的，最终都被最后一次比较的结果覆盖。说白了最终dp[i][j]的值就是最后一次循环中比较后的较大值。

正确代码：

方法一

#include<bits/stdc++.h>

using namespace std;

const int N=1010;

int n,m,v[N],w[N],dp[N][N];

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>v[i]>>w[i];

    for(int i=1;i<=n;i++)
      for(int j=1;j<=m;j++)
      {
          dp[i][j]=max(dp[i][j],dp[i-1][j]);
          for(int k=1;k*v[i]<=j;k++)//等价于max(dp[i-1][j-k*v[i]+k*w[i]),k=0,1,2,...)
          {
              dp[i][j]=max(dp[i][j],dp[i-1][j-k*v[i]]+k*w[i]);
          }
      }


    cout<<dp[n][m];

    return 0;
}

方法二

#include<bits/stdc++.h>

using namespace std;

const int N=1010;

int n,m,v[N],w[N],dp[N][N];

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>v[i]>>w[i];

    for(int i=1;i<=n;i++)
      for(int j=1;j<=m;j++)
        for(int k=0;k*v[i]<=j;k++)//等价于max(dp[i-1][j-k*v[i]+k*w[i]),k=0,1,2,...
        {
            dp[i][j]=max(dp[i][j],dp[i-1][j-k*v[i]]+k*w[i]);
        }

    cout<<dp[n][m];

    return 0;
}