BLOG

数论是用来研究整数的性质的。

• 整数集 $Z: \{..-2, -1, 0, 1, 2…\}$
• 自然数集$N:\{0, 1, 2, 3,4 …\}$

整除：

存在整数 $k$，使得$a = kd$，则称$d | a$（$d$ 整除 $a$）。

• $d$为$a$的约数，$a$为$d$的倍数。
• 任何数都是$0$的约数。

公约数

存在一个整数$d$，使得$d\ |\ x, d\ |\ y$，则$d$为$x, y$的公约数。

最大的一个称之为最大公约数，记作$gcd(x, y)$。

几个推论

1. 若$d\ |\ a, d\ |\ b$，则$d\ |\ ax + by$，其中$a, b$均为整数。
2. $gcd(xn, yn) = n * gcd(x,\ y)$
3. 若$n\ | xy$ 且$gcd(n, x) = 1$，则$n\ |\ y$。

$gcd(a, b)$ 为 $ax + by$ 的最小正整数线性组合

证明：

设 $s$ 为 $ax + by$ 是最小正整数的线性组合

由之前的$2$推论可得，$s | a, s | b$，即$gcd(a, b) <= s$

① $a \% s = a - \lfloor \frac{a}{s} \rfloor * s$

设$q = \lfloor \frac{a}{s} \rfloor$

① = $a - q(ax + by) = a(1 - qx) + b(-qy)$

因$0 <= a\ \%\ s < s $。又$s$为最小正整数解

所以① $=\ a \% s = 0$，即$s\ |\ a$。

同理$s\ |\ b$。

所以$s <= gcd(a, b)$。

由第一步的$gcd(a, b) <= s$。我们得到：

$s = gcd(a, b)$

素数定理

$[1, N]$中素数的个数约为$\frac{N}{lgN}$。则从$[1, N]$中人选一个数，其为质数的概率为$\frac{1}{lgN}$。

素数的判断

试除法：$O(\sqrt{n})$

原理：约数成对出现（完全平方数除外）

算数基本定理

任意一个整数都能被分解为如下形式：

$n = p_1^{k_1}p_2^{k_2}…p_t^{k_t}$。其中$p$为质数。

$t, \sum_{i = 1}^{t}k_i$都是$logn$量级的。

欧拉函数

$φ(n)$表示小于等于$n$中与$n$互质的数的个数

$φ(n) = n\prod_{p | n}(1 - \frac{1}{p})$ 其中$p$为质因子。

用质因子的方法，$O(\sqrt{n})$算出一个数的欧拉函数：

int phi = x;
for(int j = 2; j * j <= x; j++){
    if(x % j == 0){
            phi = phi / j * (j - 1);
            while(x % j == 0) x /= j; 
        }
}
if(x > 1) phi = phi / x * (x - 1);

$O(n)$用线性筛$[1, n]$内所有$φ$值

大概长这样：

phi[1] = 1;
for(int i = 2; i <= n; i++){
    if(!st[i]) primes[tot++] = i, phi[i] = i - 1;
    for(int j = 0; i * primes[j] <= n; j++){
        st[primes[j] * i] = true;
        if(i % primes[j] == 0){
            phi[primes[j] * i] = primes[j] * phi[i];
            break;
        }
        phi[primes[j] * i] = (primes[j] - 1) * phi[i];
    }
}

原理：质数$p$的欧拉函数为$p - 1$。线性递推即可。

扩展欧几里得

原理：裴蜀定理

扩展欧几里得算法可以$O(loga)$的时间算出：

$ax + by = gcd(a, b) (a, b > 0)$的一组解。

int exgcd(int a, int b, int &x, int &y){
    if(b == 0){
        x = 1, y = 0;
        return a;
    }
    int d = exgcd(b, a % b, y, x);
    y -= a / b * x;
    return d;
}

原理：递推

$ax + by = bx_0 + (a \% b)y_0)$

已知$a, b, x_0, y_0$，求$x, y$。

$ = bx_0 + (a - \lfloor \frac{a}{b} \rfloor * b)y_0)$

$ = ay_0 + b(x_0 - \lfloor \frac{a}{b} \rfloor * y_0)$

通解

设$d = gcd(a, b)$，扩展欧几里得算法求出的是$ax_0 + by_0 = d$，则：

• $x = x_0 + k\frac{b}{d}$
• $y = y_0 + k\frac{a}{d}$

其中$k$为任意整数。

$x, y$的分布规律可看做一条一次函数：

正整数解：$x, y >= 0$。

若我们想正整数解（$x, y >= 0$）中$x$的最小值，只需$\% \frac{b}{d}$，但是$C++$中会膜成负数和$0$，所以还需要特判：

• $x = (x0\ \% \frac{b}{d} + \frac{b}{d}) % \frac{b}{d}$
• $if\ x == 0\ then\ x += \frac{b}{d}$

此时对应的$y$即正整数解范围内的$y$最大值，想判断其是否存在正整数解，只需判断对应的$y > 0$即可。

求$y$的最小值与$x$的最大值同理。

在正整数解内分布个数

先搞到$x$的最小正整数解$x0$，此时对应的$y0 = (d - ax0) / b$

那么考虑其实是可以往下等距缩，即：

$cnt = \lceil y0 /\frac{a}{d} \rceil$

一般套路

亦或是同余方程，还是其他玩意，你可以转化为：

$ax + by = c$。

此时先把$d = ax + by = gcd(a, b)$的$x, y$用扩展欧几里得算出来。

• 若$c \% d \not= 0$ 无解
• 否则，把对应的$x, y$都扩大$c / d$倍，可以就按照刚才的来做啦。

$O(n)$预处理$[1, n]$内所有数的阶乘及其逆元

因为$(i!)^{-1} = \frac{1}{i!} = \frac{i + 1}{(i+ 1)!}$

所以先把$infact_n$算出后，得到递推公式：

$infact_i = infact_{i + 1} * (i + 1)$

组合数

把杨辉三角搞出来以后有一些奇怪的规律。

1. 自左上（顶端）向右下一连串的和$=$其最右端再往下一个的值

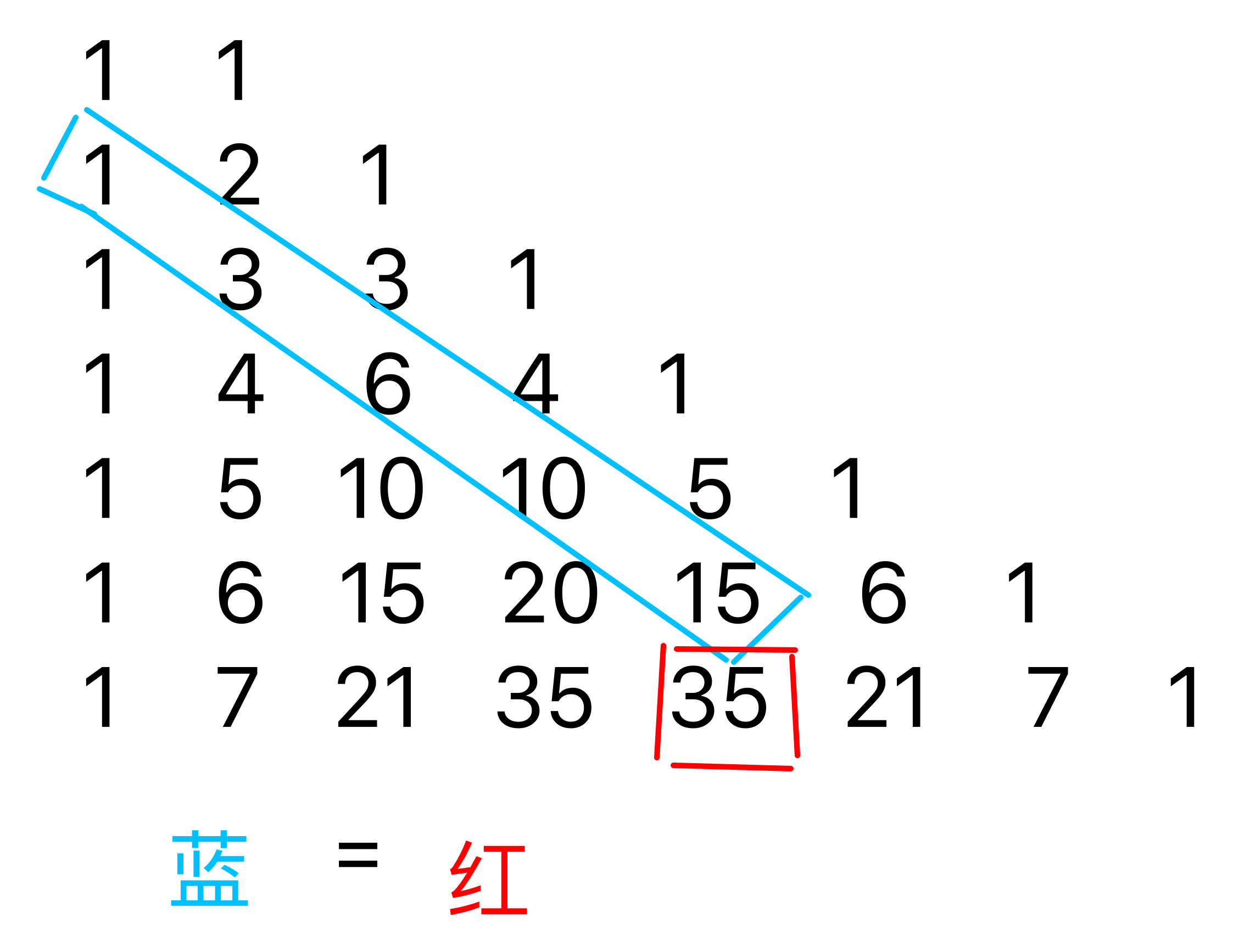
1. 一列的总和$=$最下端右下角的值